奇异（k，n－k）共轭多点边值问题方程组的正解

江卫华，陈志红

（河北科技大学理学院，河北石家庄 050018）

奇异（k，n－k）共轭多点边值问题方程组的正解

江卫华，陈志红

（河北科技大学理学院，河北石家庄 050018）

对固定的1≤k≤n－1，运用锥拉伸与锥压缩不动点定理，研究了具有奇性的（k，n－k）共轭多点边值问题方程组正解的存在性。

奇异；（k，n－k）共轭多点边值问题；正解；不动点定理

在文献［1］中，蒋达清等对奇异（k，n－k）共轭2点边值问题

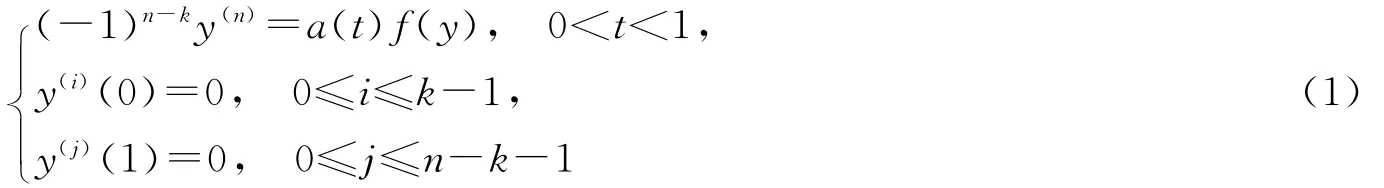
进行了讨论，并在超线性和次线性的条件下，运用锥拉伸与锥压缩不动点定理，得出了该方程的正解存在性。在文献［2］中，蒋达清又对此问题进行了更进一步的研究，给出了格林函数的精确表达式。

在文献［3］中，张国伟等应用不动点指数理论，得到了奇异（k，n－k）共轭边值问题（－1）n－kφ（n）（x）＝h（x）f（φ（x）），0＜x＜1，n≥2，1≤k≤n－1分别在边界条件：

下正解的存在性结果。对方程组的研究也已有很多结果，读者可参见文献［4］—文献［9］，但对（k，n－k）共轭多点边值问题方程组的研究，据笔者所知还未有结论。

受到以上文献的启发，笔者讨论多点奇异（k，n－k）共轭边值问题方程组

下面的锥拉伸与锥压缩不动点定理，是本文的关键定理，其证明可见文献［7］。

1 主要引理

引理1［2］方程（1）的格林函数为

引理4［3］假设Ⅰ）、Ⅱ）成立，则算子T为全连续算子。

证明 要证T为全连续算子，只需证明T1，T2全连续。下面给出T1全连续的证明，记作

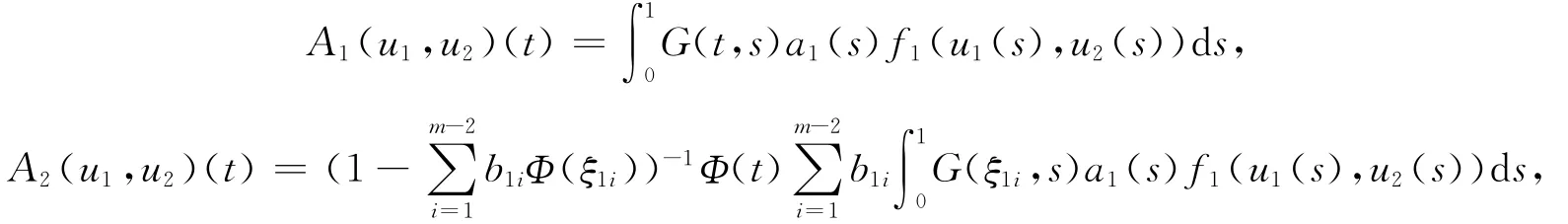
于是T1＝A1＋A2，由文献［2］知A1为全连续算子，易见A2为全连续算子，所以T1全连续。用类似的方法，可以得出T2全连续。所以算子T为全连续算子。

2 主要结果

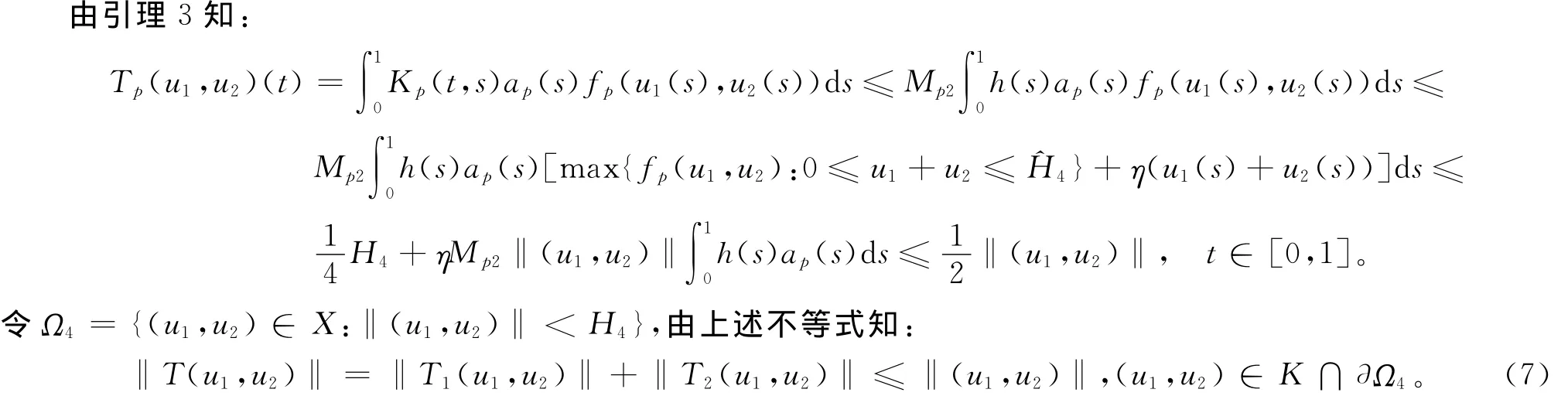
所以，由式（6）、式（7）和定理1知，算子T在P∩（¯Ω2＼Ω1）中有1个不动点。证毕。

注：考虑函数f1（x，y）＝｜sin（x＋y）｜＋｜cos（x＋y）｜，f2（x，y）＝e－（x＋y），显然，当（x，y）∈［0，＋∞］×［0，＋∞］时，函数连续、非负，且满足假设条件Ⅳ）。

［1］ JIANG Da－qing，LIU Hui－zhao．Existence of positive solutions to（k，n－k）conjugate boundary value problems［J］．Kyushu J Math，1999，53（1）：115－125．

［2］ 蒋达清．奇异（k，n－k）共轭边值问题的正解［J］．数学学报（Acta Mathematica），2001，44（3）：541－548．

［3］ 张国伟，孙经先．奇异（k，n－k）多点边值问题的正解［J］．数学学报（Acta Mathematica Sinica），2006，49（2）：391－398．

［4］ XI Shou－liang，JIA Mei，JI Hui－Peng．Positive solutions of boundary value problems for systems of second－order differential equations with integral boundary condition on the half－line［J］．Electronic Journal of Qualitative Theory of Differential Equations，2009，31：1－13．

［5］ HU Ling，WANG Liang－long．Multiple positive solutions of boundary value problems for systems of nonlinear second－order differential equations［J］．J Math Anal Appl，2007，335：1 052－1 060．

［6］ JIANG Wei－hua，CHEN Zhi－hong．Positive solutions for systems of two－point（k，n－k）conjugate boundary value problems［A］．2010 First International Conference on Cellular，Molecular Biology，Biophysics and Bioengineering［C］．［s．L．］：［s．n．］2010．420－422．

［7］ KRASNOSELSKII M．Positive Solutions of Operator Equations［M］．Groningen：Noordhoof，1964．

［8］ 王 斌，江卫华，黄晓芹，等．带有p－Laplacian算子的二阶微分方程组多个正解的存在性［J］．河北科技大学学报（Journal of Hebei University of Science and Technology），2011，32（1）：15－19．

［9］ 董士杰，周长杰．带p－Laplacian算子时滞微分方程多点边值问题的正解［J］．河北科技大学学报（Journal of Hebei University of Science and Technology），2010，31（5）：385－389．

Positive solutions to system of singular（k，n－k）conjugate multi－point boundary value problems

JIANG Wei－hua，CHEN Zhi－hong
（College of Sciences，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

As 1≤k≤n－1，by using the fixed－point theorem of cone expansion and compress，the existence of positive solutions to a system of singular（k，n－k）conjugate multi－point boundary value problems is studied．

singular；（k，n－k）conjugate multi－point boundary value problem；positive solutions；fixed－point theorems

O121

A

1008－1542（2011）04－0303－05

2011－03－06；责任编辑：张 军

江卫华（1964－），女，河北邯郸人，教授，博士，主要从事应用泛函分析、常微分方程边值问题方面的研究。