多导体传输线非线性负载响应的FDTD模拟

胡 凯，赵 翔，闫丽萍，刘长军，黄卡玛

（四川大学电子信息学院，四川成都 610064）

多导体传输线非线性负载响应的FDTD模拟

胡 凯，赵 翔，闫丽萍，刘长军，黄卡玛

（四川大学电子信息学院，四川成都 610064）

多导体传输线（MTLs）对激励信号非线性响应的仿真研究在电磁兼容分析和电磁效应评估研究中具有重要作用。本文采用FDTD方法研究集总源对端接非线性负载的MTL的影响，推导出电报方程的差分格式与边界条件，计算得到了MTL上电压波和电流波的瞬态响应情况，所得结果和已有文献中利用时域BLT方法算出的结果完全吻合。

多导体传输线；非线性负载；瞬态响应；时域有限差分

多导体传输线（MTLs）是电子系统中射频能量传输的重要途径，因此MTL对激励信号响应的仿真研究在电磁兼容分析和电磁效应评估研究中具有重要作用［1］。由于电子系统中非线性元器件的广泛使用，对MTL上非线性负载的非线性响应过程研究就显得很有必要，为此在时域对MTL方程进行求解是合理且可行的。本文采用时域有限差分（FDTD）方法研究集总源对端接非线性负载的MTL的影响，推导出电报方程的差分格式与边界条件，计算并验证了已有文献中利用时域BLT方法算出的结果。

1 多导体传输线方程及其FDTD方法

不考虑外界电磁场作用的情况下，在如图1a）所示的MTL上，电流波向量［Ii（z）］和电压波向量［Vi（z）］满足电报方程［2］

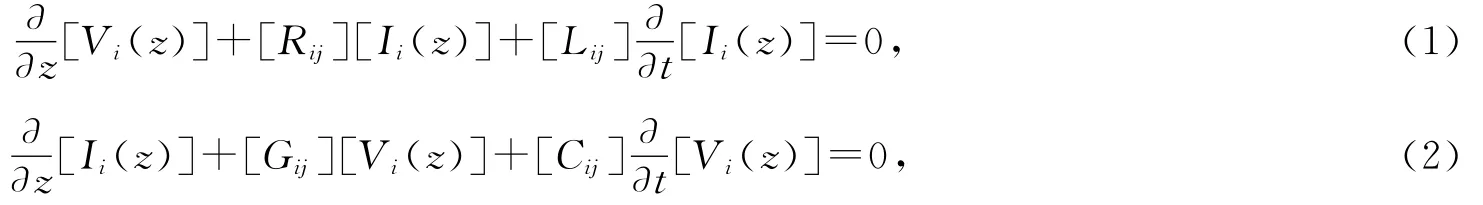
其中i，j＝1，2，…，N－1；N为导体个数。［Rij］、［Lij］、［Gij］和［Cij］分别是（N－1）×（N－1）阶的单位长度电阻、电感、电导和电容矩阵。对于无耗三导体线［3］（设导线0为接地线），有

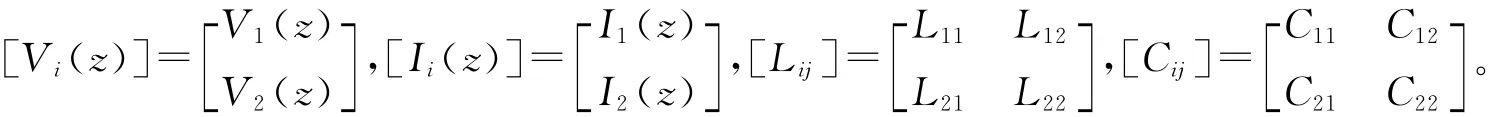
采用FDTD方法进行方程（1）和（2）的求解。将传输线长等分为K段，采用差分格式对微分方程在时间和空间上进行离散［4］。

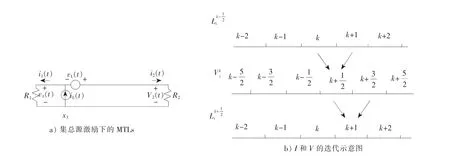
图1 MTL及其电流电压的迭代

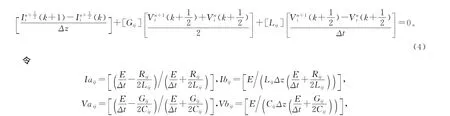
得到最终的迭代格式（参见图1b））：

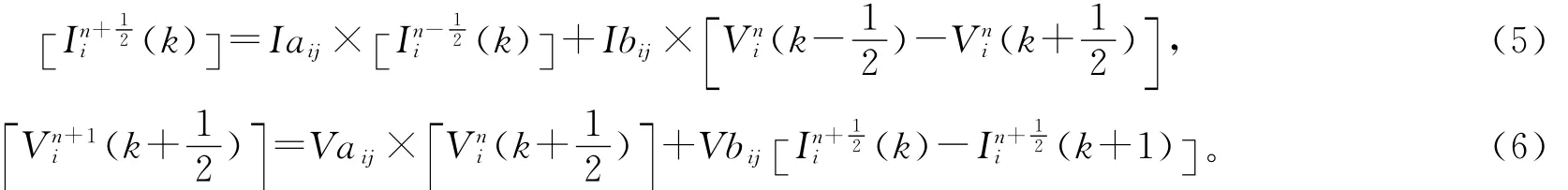
为保证迭代过程的稳定性，时间步长应足够小，满足约束条件［5］：

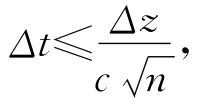
其中，n是对应空间的维数，V是MTL上电波传播速度。

2 计算实例

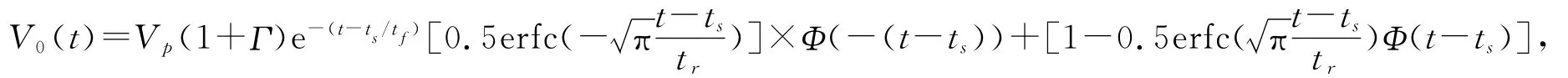
式中erfc（·）是误差宗量函数，Φ（·）表示单位阶跃函数。波形的峰值电压VP＝10 k V，其中常量Γ＝0．024，tr＝100 ps，tf＝4 ns，ts＝0．2 ns。同轴线内、外导体半径分别为a＝2．5 mm和b＝9．345 mm，并且外导体厚度为tk＝0．6 mm，内外导体之间填充相对介电常数εrel＝2．5的介质，可以求得该同轴线的特征阻抗为50Ω。在同轴线左端和右端分别接上R1＝10Ω和R2＝100Ω的负载电阻，相应的边界条件为

经过约15 000个时间步的计算，获得如图2a）所示的负载响应结果。

例2：设例1中右端负载R2为非线性负载，其非线性特征由下式给出。

利用上述方法并结合一定的边界条件来计算MTL端接线性负载（例1）和非线性负载（例2）的实例［1］。

例1：如图1a），一长度为L＝1 m且集总电压源接在xs＝0．2 m处的同轴传输线，其表达式如下：

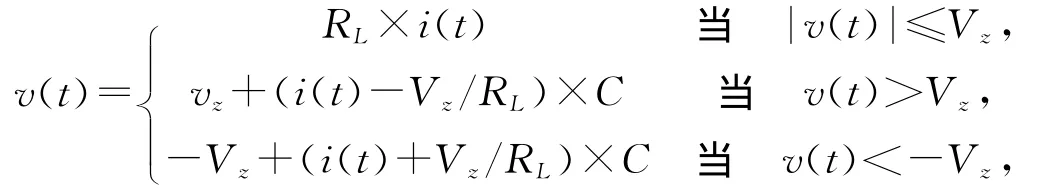
其中C＝1，Vz＝2 000，RL＝100。同理可得右端非线性负载的响应情况，如图2b）。

图2所示的计算结果和已有文献［5－6］中利用时域BLT方法得到的结果完全吻合。

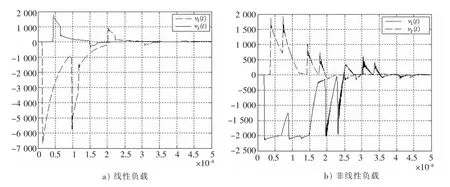
图2 负载电压的瞬态响应

3 结 语

采用FDTD方法研究集总源对端接非线性负载的MTL的影响，推导出电报方程的差分格式与边界条件，计算得到了MTL上电压波和电流波的瞬态响应情况，所得结果和已有文献中利用时域BLT方法算出的结果完全吻合。对场线耦合情况下的仿真将在后续工作中通过施加分布式电压源和电流源来实现。

［1］ BAGCI H，YILMAZ A E，MICHIELSSEN E．An FFT－accelerated time－domain multiconductor transmission line simulator［J］．IEEE Trans Electromagn Compat，2010，52（1）：15－25．

［2］ PAUL C R．Incorporation of terminal constrains in the FDTD analysis of transmission lines［J］．IEEE Trans Electromagn Compat，1994，36（2）：85－95．

［3］ 李 莉，冀维林．端接非线性负载的不等长传输线瞬态分析［J］．电波科学学报，2009，24（3）：529－532．

［4］ POLLARD R D B．Electromagnetic Simulation Using the FDTD Method［M］．New York：Sullivan D M，2000．

［5］ TESCHE F M．Development and use of the BLT equation in the time domain as applied to a coaxial cable［J］．IEEE Trans Electromagn Compat，2007，49（1）：101－115．

［6］ TESCHE F M．On the analysis of a transmission line with nonlinear terminations using the time dependent BLT equation［J］．IEEE Trans Electromagn Compat，2007，49（2）：11－26．

O451

A

1008－1542（2011）12－0178－02

2011－06－20；责任编辑：王士忠

国家自然科学基金青年基金资助项目（60801035）

胡 凯（1985－），男，四川宜宾人，硕士研究生，主要从事计算电磁学方面的研究。