ESD EMP干扰下电路端口响应分析
2011-12-28刘卫超樊高辉谢文强
刘卫超,魏 明,樊高辉,谢文强
(军械工程学院电磁环境效应重点实验室,河北石家庄 050003)
ESD EMP干扰下电路端口响应分析
刘卫超,魏 明,樊高辉,谢文强
(军械工程学院电磁环境效应重点实验室,河北石家庄 050003)
为了探寻电路在静电放电电磁脉冲(ESD EMP)干扰激励下的响应规律以及响应输出与输入脉冲干扰之间的关系,选用运算放大器集成芯片组成的仪表放大电路进行了脉冲注入实验。根据采集的实验数据,分析了注入脉冲与响应输出之间的关系。根据系统辨识理论,建立了能量耦合模型。经过自验证,其拟合度能够达到94.3%,且具有较好地泛化能力,能够对电路的响应做出定性预测。
电子设备;ESD EMP;干扰;响应分析
静电是自然环境中最普遍的电磁脉冲辐射源,静电放电可以产生强烈的电磁辐射而形成宽频带电磁脉冲场,形成静电放电电磁脉冲(ESD EMP)[1]。而由于电子设备在各个科学技术领域、工业生产部门应用十分广泛,尤其伴随着集成度的提高、门限电压的降低,电子设备对恶劣的环境影响也越来越敏感[2]。因此,对电子设备进行ESD EMP干扰下的工作情况进行评估是十分必要的。电子设备效应评估包括效应实验和仿真预测两方面。在效应实验的基础上,能够通过仿真预测对电子设备在脉冲激励下的响应输出做出合理的预测。目前,电子设备电磁脉冲效应仿真包括基于机理分析和基于实验数据统计2种效应仿真方法,后一种方法因目前电子设备内部结构较为复杂,其内部机理越来越难以掌握而应用更为广泛[3]。基于实验数据统计的方法主要原理是电子设备的脉冲能量耦合通道的动态特性能够通过脉冲激励、电子设备响应数据反映出来,根据实验数据建立的脉冲能量耦合模型,能够在一定程度上反映出电子设备电磁脉冲干扰下的响应情况,并可做出预测。
实验数据中包含着大量输入、输出之间的必然联系,通过研究端口响应波形与输入电磁脉冲之间的关系,可以对脉冲能量耦合模型的正确与否进行评判,并且对将模型应用于电子设备电磁脉冲效应预测方面具有一定的指导意义。
笔者以某模拟放大器电路为例,对其进行了ESD EMP注入实验,并对实验结果进行分析,摸索电路功能模块响应输出与脉冲激励参数之间的关系。根据采集的实验数据,建立了基于神经网络系统辨识理论的系统能量耦合模型,并通过改变网络结构参数,使模型具有较高的泛化能力。
1 ESD EMP注入实验与分析
1.1 实验设计
被试电路为由型号为LM324的运算放大器组成的仪表放大电路,其转换特性为
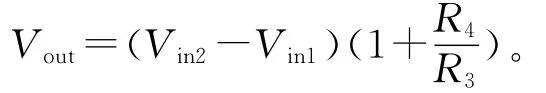
此电路在各类智能仪器仪表中应用比较广泛,它可将仪表初步测到的信号放大并提高信噪比[4]。当其在ESD EMP干扰下产生非预期输出时,必然对下级电路产生影响。因此,掌握其在ESD EMP环境中的响应情况是十分必要的。
如图1所示,利用静电放电模拟器(SANKI NS61000-2A型,输出电压为0.2~30 k V,正负极性可调)产生静电放电电磁脉冲,并将其通过接触式放电的方式输入到被试电路输入端,将被试电路耦合的脉冲信号从输出端经过20 dB脉冲衰减器传输到高性能数字存储示波器(Tektronix,7154B型,1.5 GHz,20 GSa/s);同时通过60 dB脉冲衰减器将电路输入端耦合的静电放电脉冲输入信号传输到高性能数字存储示波器,进行数据采集存储。通过改变脉冲幅值,取得多组不同脉冲干扰下产生的响应情况。图2为示波器实测波形。
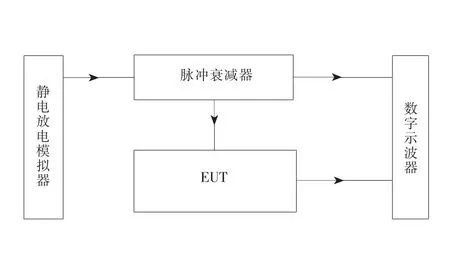
图1 实验原理图

图2 ESD EMP注入实验输入与输出
1.2 实验结果分析
通过实验实测波形可以看出,电路响应输出受脉冲峰值影响较大,且在同一时刻达到最大值。输入输出都叠加了一定程度的噪声。静电脉冲模拟器输出电压、电路输入端口耦合电压、电路响应电压实测数据如表1所示。

表1 响应电压与输入电压之间的关系
从实验采集的多组波形互相比较可以看出,电路端口响应波形大致趋势是一致的,在注入脉冲幅值变化的同时,并没有发生较大的变化。随着ESD EMP辐值的增大,耦合到输入端口的电压增大,响应电压的峰值也在升高,且基本成线性关系,说明此电磁脉冲能量耦合系统为一个线性系统。从电路角度看,组成元件多为线性元件,耦合的能量通过电路传输到下一级,并在传输过程中逐渐衰减。
2 基于神经网络的能量耦合建模
基于系统辨识理论的电磁脉冲效应仿真在相关文章中已经做了探索,并得到较好的仿真结果。此方法是结合实验测试与理论建模相结合的一种方法,其将系统视为“黑箱”,利用采集的实验数据确定能量耦合模型的各参数,找到一个比较理想的模型逼近实际系统[5]。
笔者选用NARX神经网络模型进行建模,NARX模型是一个周期性循环的动态网络,它带有一个后向反馈,使网络闭合为一个循环线路[6-7],图3为其结构图。通过训练,将电磁脉冲能量耦合、电路响应这一系统的特性规律记忆在网络权值中,并通过评价样本数据对模型预测值与真实值的拟合度进行检验。
在建立模型之前,为了提高模型精度,首先要对所采集到的实验数据进行预处理。在采集的实验数据中,包含着高频与低频噪声成分,它们并不反映被试电路电磁脉冲能量耦合系统的系统特性,因此可以利用小波降噪将其剔除。通过选择合适的小波基函数和分解层次对信号进行分解,然后设定阈值,将小于等于阈值的高频系数置零,大于阈值的保留,这样既保持了信号的细节又达到了降噪目的。
利用MATLAB编程建立一个2层的NARX神经网络模型,设定模型的输入/输出延时阶次为2,隐含层传递函数为tansig,输出层函数为purelin,训练函数使用trainbr,训练目标为0.01,隐含层神经元数为30。迭代次数分别选择30,50,70,100进行训练,发现超过50后,误差性能并没有改善,为了降低训练时间,迭代次数定为50。利用采集到的4 k V静电放电电磁脉冲耦合信号及响应输出作为建模数据,对神经网络模型进行训练。
如图4所示,训练结束后,利用建模数据进行自验证,发现其预测输出与实验测得响应输出的拟合度可达到94.3%,说明此模型应用于响应预测这一领域是十分有效的。
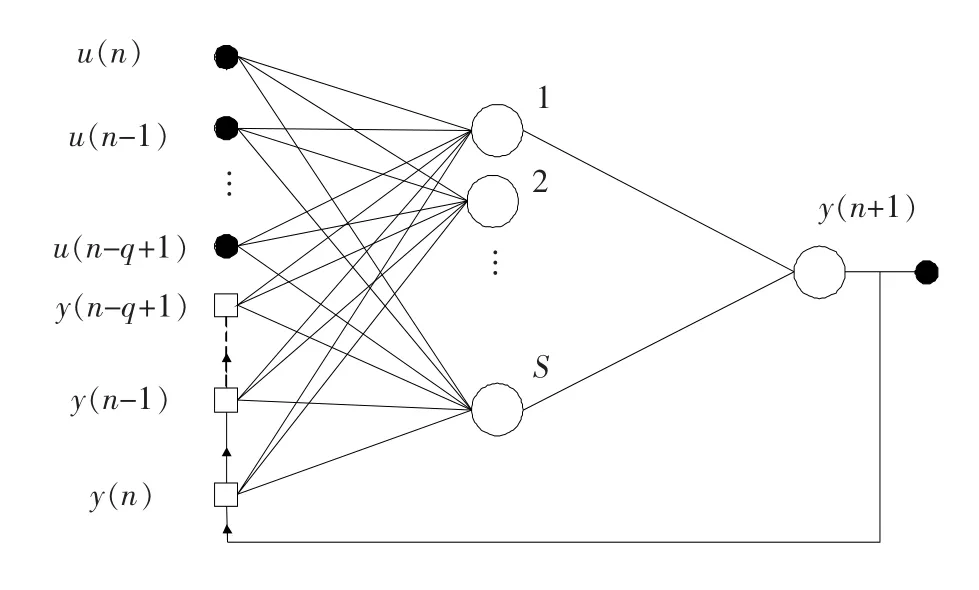
图3 NARX神经网络模型结构
将6 k V ESD放电电流信号代入系统辨识所得传递函数,得到模型输出与实验输出对比关系图(见图5),拟合度达到90.6%。从图5中可以看出,模型预测曲线虽然在细节上与实验曲线有较小差别,但大体走势一致,尤其对响应波形的峰值、上升时间、响应波形的平均振荡周期等重要特征预测得比较准。而作为电磁干扰源,ESD对辐射场影响最大的是放电电流的起始部分,EUT(equipment under test)响应电压最大值也在起始部分,因此该模型对于ESD EMP响应预测具有重要意义。
3 结 语

图4 4 k V模型输出与实验输出对比图

图5 6 k V模型输出与实验输出对比图
在典型仪表放大器电路ESD EMP注入实验的基础上,分析了电路响应与静电放电耦合电压之间的关系,并建立了电磁脉冲能量耦合模型。通过验证可以发现,模型自验证拟合度可达到94.3%,且具有较好泛化能力。模型能够较准确地预测出响应电压的峰值、上升时间等特征,且大致变化趋势与实验结果一致,说明此模型可以较好地反映此实验中的被试电路能量耦合系统特性。
此方法可以应用于典型电路电磁脉冲响应预测,并且结合实验结论,对电路模块的电磁脉冲敏感度预测分析提供依据。
[1] 刘尚合,武占成.静电放电及危害防护[M].北京:北京邮电大学出版社,2004.
[2] 周 星,张成怀,魏光辉.电磁脉冲与连续波对数字电路的辐照效应比较[J].高电压技术,2010,36(7):1 761-1 766.
[3] 魏 明.设备级电磁脉冲效应仿真算法研究综述[J].军械工程学院学报,2009,21(6):50-53.
[4] 崔利平.仪表放大器电路设计[J].现代电子技术,2009(11):87-89.
[5] 魏 明,杨 楠,王向东,等.静电放电电磁脉冲能量耦合的系统辨识建模[J].高电压技术,2010,36(8):2 017-2 022.
[6] 张国梁,张志杰,杜红棉,等.基于NARX神经网络的冲击加速度计建模研究[J].弹箭与制导学报,2008,28(3):284-286.
[7] 柴琳娜,屈永华,张立新,等.基于自回归神经网络的时间序列叶面积指数估算[J].地球科学进展,2009,24(7):756-766.
O441.1
A
1008-1542(2011)12-0168-03
2011-06-20;责任编辑:张士莹
刘卫超(1984-),男,山东肥城人,硕士研究生,主要从事电磁仿真与效应评估技术方面的研究。
