复杂形体的瞬态电磁场计算技术研究

任 武，薛正辉，王学田，李伟明，房丽丽

（北京理工大学信息与电子学院微波技术研究所，北京 100081）

复杂形体的瞬态电磁场计算技术研究

任 武，薛正辉，王学田，李伟明，房丽丽

（北京理工大学信息与电子学院微波技术研究所，北京 100081）

以时域有限差分法（FDTD）为复杂形体瞬态电磁场分析的核心算法，针对电大尺寸、复杂形体的建模技术、网格剖分技术展开了研究和分析，给出一些仿真的实例，从精确度、仿真效果等方面加以说明该算法的适用性。可以看出，FDTD方法非常适合于该类瞬态电磁场的分析，还给出了下一步应重点解决的关键技术。

电磁兼容；时域有限差分法；复杂形体；网格剖分

随着电子科学技术的快速发展，电子设备的电磁兼容性问题也逐渐变得突出。对于复杂平台，如飞机、舰船、战车、导弹、卫星，在上面工作的电子设备越来越多、越来越密集，如果电磁兼容性发生问题，结果将是灾难性的。电磁兼容问题分为系统间电磁兼容问题和系统内电磁兼容问题，需要从系统级、分系统级、设备级、电路级等多个层次展开研究。因此电磁兼容预测是必不可少的环节，就是通过理论计算对安装的设备或系统的电磁兼容程度进行分析评估。其目的是为了分析不兼容的薄弱环节，评价系统或设备兼容的安全裕度，为方案修改、防护设计提供依据。同时在研制定型之前通过预先测知发现干扰问题，采取抑制和防护干扰措施。

目前通过大量的电磁场环境的分析计算来进行电磁兼容的研究成为发展的趋势，如天线间耦合干扰的计算、电缆辐射特性等。随着需求的提升，需要一些高精度的电磁场数值算法来研究复杂电磁环境的变化规律，对电大尺寸近区的电磁场可以进行仿真，完整分析耦合干扰通道和干扰效能。目前在电磁场分析领域有不少通用软件，如Ansoft公司开发的以矩量法和有限元为基础的HFSS电磁场、基于时域有限积分法的CST软件等，但在应用中还存在很多局限性，如对于各种外来的特殊电磁干扰也往往无法加入到模型中，某些中间场值无法提取等。因此，要想全面地研究和预测复杂平台上的电磁场分布、变化规律和传播特性，就要提高仿真和分析的手段，与目前电磁学的仿真分析技术研究紧密联系在一起［1－4］。

时域有限差分法（finite－difference time－domain method，FDTD方法）是有限差分类型方法的一个重要分支，20世纪70年代中期就进行电磁兼容（EMC）问题的分析与预测，用于分析处在高压电磁脉冲环境中的飞机机身表面的场分布和预测飞机内部耦合场干扰情况。它是以时域麦克斯韦微分方程为数学模型，对这种数学模型进行差分离散化而构造的一种数值计算方法。自FDTD方法提出以来，其应用领域已从早期的电磁散射，迅速推广到生物电磁学、微波电路分析设计、电磁兼容预测、电波传播与天线辐射问题等，时至近日，仍然是一种较为先进的数值分析方法。FDTD方法由于其对复杂媒质进行建模和能进行时域分析的能力，一直在电磁兼容预测中起着重要作用，尤其在分析复杂结构以电磁场耦合、传导、辐射和散射为基础的电磁干扰方面具有无可比拟的优势。该算法直接在时域进行计算，可以得到宽频带特性，特别对于雷电等脉冲具有很好的仿真效果，是研究瞬态电磁场的最佳算法。

1 FDTD计算速度的发展

FDTD算法相比其他算法，对存储的要求是比较低的，但是该方法也需要将计算空间离散化，每个网格上的场量都需要存储，这样随着分析结构的复杂化、分析目标尺寸的增大，FDTD法会越来越受到计算平台的限制。随着计算机本身的更新换代，计算速度与几年前相比有了质的飞跃，但是用来计算复杂形体还是非常费时间的甚至无法算下来。从20世纪90年代初期开始已经相继有FDTD并行运算方面的论文问世。并行的目的就是为了使不能由单机运行的计算量，通过并行实现，使分配给每个节点的计算量在单机可计算的承受范围内，从而实现大存储量的计算分析。

2003年，笔者提出了FDTD方法在微机互连构成的机群（COW）并行计算系统上以消息传递方式执行的一种实现方案，组成了验证性的机群并行计算系统，成功编写了并行计算程序，得到了良好的加速比和并行效率。组建了1主控节点＋16计算节点的专用并行FDTD运算系统，采用星形连接。

适应于各个计算节点分别承担一部分计算任务，原来串行FDTD计算中待分析目标形体的整个模型必将要分割成与各计算节点对应的各部分。这一点一般来说并不困难，因为FDTD计算模型本身就是离散化的数字模型，按照要求的划分方式‘肢解’计算模型即可。图2表示了待分析的一实心圆球的模型分割，分割数是3段。

近年来，随着图形处理器（GPU）运算能力的高速增长及GPU通用运算概念的提出，利用GPU辅助科学计算已成为一个重要趋势。举例来说，一块型号为NVIDIA Tesla C2050的GPU具有448个流数据处理器，具有达到1040GFLOPS单精度502G双精度的浮点运算能力，而最新Intel i5 CPU浮点运算能力仅为42GFlops。

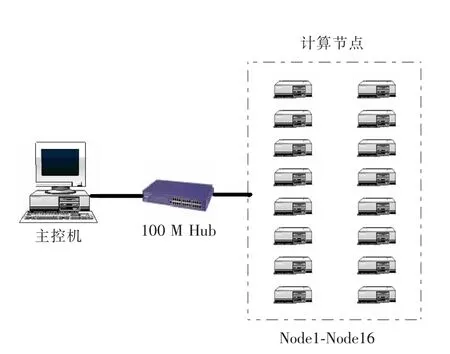
图1 PC机群系统示意图

在电磁场数值计算领域，2004年KRAKIWSKY等即实现了利用GPU加速电磁场FDTD运算，其后其他一些研究者也开展了开拓性的工作，美国斯坦福大学和莱斯大学，加拿大卡尔加里大学的研究者都已经广泛深入地开展了利用GPU进行电磁场数值计算的工作［5－6］。在国内，2006年，南京理工大学的李蔚清、南京电子技术研究所的杨正龙等人即开展了基于GPU的复杂目标电磁散射快速算法研究［7－8］。2007年山东大学的韩林等人开展了利用GPU结合网络并行运算技术的FDTD算法研究，针对光波导期间为分析对象进行了非常有意义的探索［9］。2008年，电子科技大学聂在平教授的课题组开展了GPU运算在快速多极子算法方面的应用研究［10］，西南交通大学的刘昆等人开展了GPU加速时域有限元的二维辐射计算研究［11］。可见国内的相关研究也正在逐步展开，并且日渐活跃。至今，相关研究者已经公认，GPU运算时代正在来临，基于GPU运算的相关技术研究和应用必将获得极大重视。

所以从发展来看，将FDTD计算、GPU计算和并行计算结合起来，是电大尺寸、复杂形体瞬态电磁仿真的有效解决方案之一。

2 FDTD建模及网格剖分技术的研究

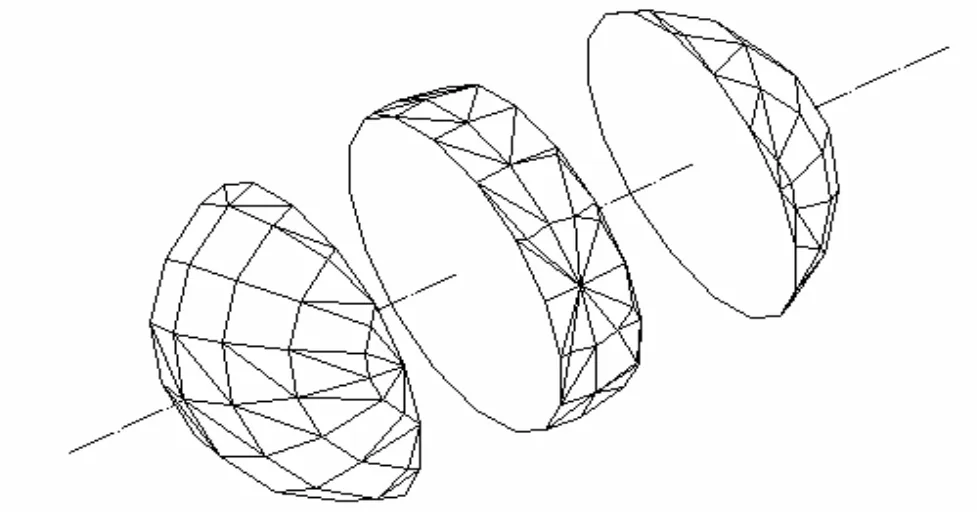
图2 FDTD计算模型的并行化分割

要进行FDTD计算，必须首先对研究目标进行建模和网格剖分，建模及网格剖分的精度直接决定了最终的分析精度。在使用FDTD仿真早期，所研究的目标大多是小型、简单物体，所以建模比较容易，网格剖分也都是采用人工完成，但是随着研究的深入，涉及到的对象往往是战车、舰船、卫星等物体，建模及网格剖分就无法纯人工去完成，需要计算机来配合实现。

在多年的研究中，笔者提出了AutoCAD辅助自动FDTD建模技术，并将该技术成熟化，特别适用于电大尺寸物体的建模中。下面以飞机的模型建立为例加以说明。

基于飞机详细结构信息的图纸，采用子域分割，将飞机实体按外部特征分割成相对独立的子块，如图3所示，把整个飞机分成机身、机翼、尾翼和发动机及挂架等模块，再将每个模块分层分段；对各层各段分别采用B样条进行拟合，生成目标图形；应用AutoCAD提供的各种生成实心体的方法生成具有足够精度的目标实心体图，具有不同电磁参数的部分可以画在不同的层上。

将生成的各部件三维实心体按照部件的相对位置进行组合，生成完整的目标实体模型。飞机的整体模型见图4。

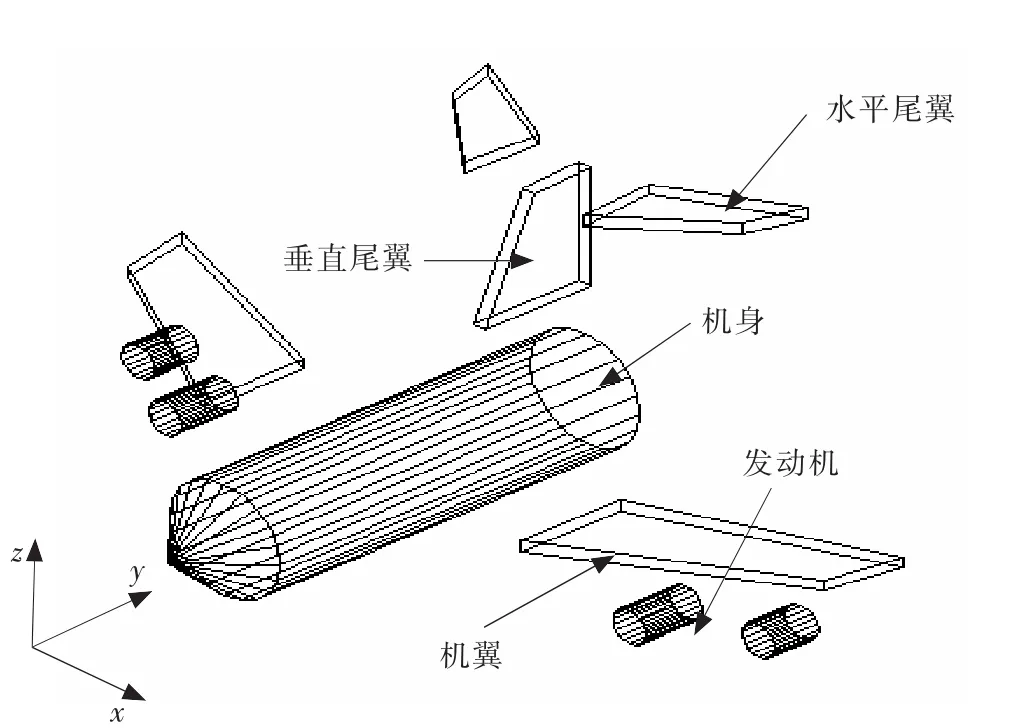
图3 飞机建模分块示意图

模型建立后，下一个重点就是网格剖分。传统方法是“网格扫描法”。具体做法是用一个立方体实心体（FDTD的网格单元）扫描包围目标的一个长方体空间，扫描过程中，不断检测扫描立方体和目标实心体模型的相交部分的体积，如果相交部分体积值大于或等于扫描立方体体积值的一半，则记下此时扫描立方体中心所在的坐标值。此方法实际上是采用阶梯式边界近似实际的边界。这种方法精确度高，但对网格剖分数量巨大的实体模型，效率太低。在应用中，提出了一种“降维处理法”。其基本思想是将待分析物体分块，根据每一块模型的外形特征，选取最佳的切割面方向，依次判断切割面与待分析模型之间有没有交集，即切割面有没有切到模型。若有交集，然后再加以判断哪些是属于物体的网格。

当被研究的物体或媒质具有曲线表面（如圆形波导、飞行器表面等），若用传统的矩形网格单元去拟合表面，就会形成‘阶梯’形边界，使用这种‘阶梯’边界不仅会激励起表面波传输，引起附加的数值色散，而且为了拟合曲率半径小或多层媒质界面，就要减小网格单元尺寸，相应的减小时间步长，从而大大增加了计算存储量，加长计算时间。针对此问题，也提出几种网格剖分技术，其中曲线坐标系下的网格剖分技术可以很好地克服“阶梯”表面引起的问题。

下面以双绞线感应电流的电磁兼容仿真为例加以说明曲线坐标系下的网格剖分技术。

图5给出了双绞线的某一横截面示意图，但是考虑到双绞线是2条线扭转的，所以适应FDTD的空间建模，应该中间是旋转的线模型，周围是不旋转的外空间相连接。实际空间仿真时的示意图见图6，曲线坐标系下的网格剖分见图7。

所以最终FDTD网格剖分如图7所示，内部适用旋转坐标系，外部适用圆柱坐标系，沿轴线每一层网格上所有的节点都按逆时针（或顺时针）旋转一个格，但是旋转后的节点与原节点是完全重合的，这样就可以顺利地与外面的空间联系起来。

图4 飞机三维实体图

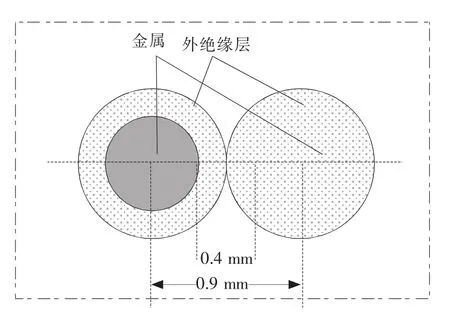
图5 双绞线的横截面示意图

图6 实际空间仿真时的示意图

3 FDTD用于计算瞬态电磁场的部分结果

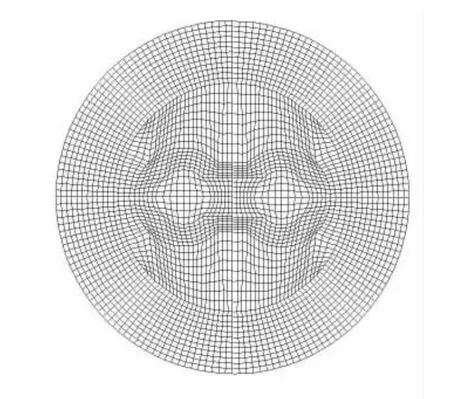
图7 曲线坐标系下的网格剖分

FDTD执行的是直接时域计算，它直接把含时间变量的麦克斯韦旋度方程转换为差分方程，所得计算结果是包含时间变量的四维数值解。这一特点使它能直接给出完整的电磁场时域信息，对电磁场的传播、散射、衍射等随时间进展的演化过程的描述非常直观，即得出直观的瞬态电磁场分布，因此是瞬态电磁场计算仿真的最佳算法之一。

FDTD仿真雷电脉冲冲击的过程示意图见图8，等离子体腔体内的电磁场分布见图9。

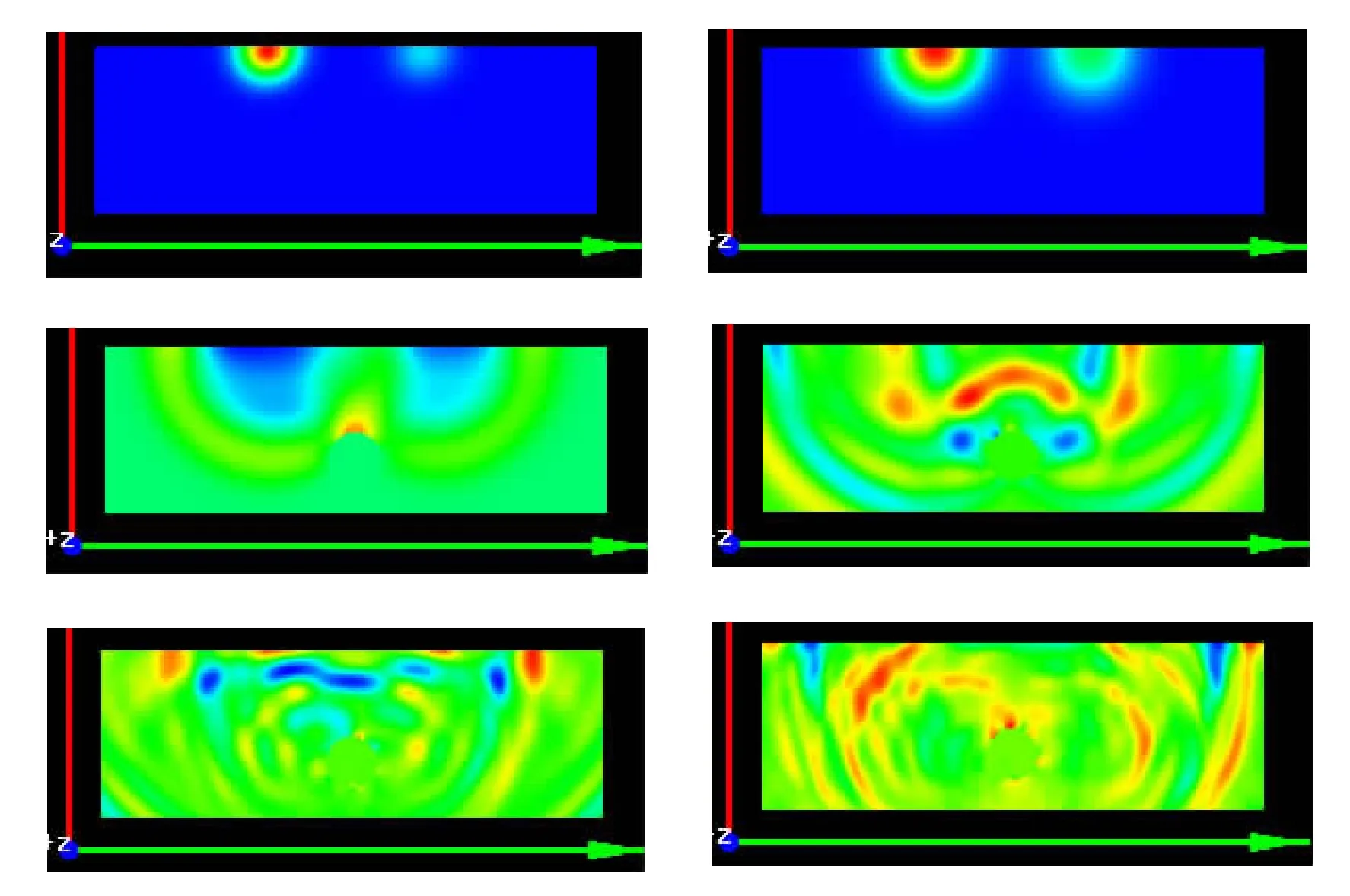
图8 冲击随时间的效应显示（各时间点间间隔顺次约为2．9 ns）

4 下一步应重点解决的关键技术

1）FDTD网格剖分技术仍然是一个需要重点研究的关键技术。FDTD算法有许多优点，但是与有限元等方法相比，其自动网格剖分技术一直是一个难点，无法实现复杂形体的高精度自动网格剖分。给出的双绞线的曲线坐标系网格剖分示意图，很大程度上靠研究人员自己去剖分，很费时间，所以高精度并且占用最小存储量的网格剖分技术是必须首先得以解决的难题。

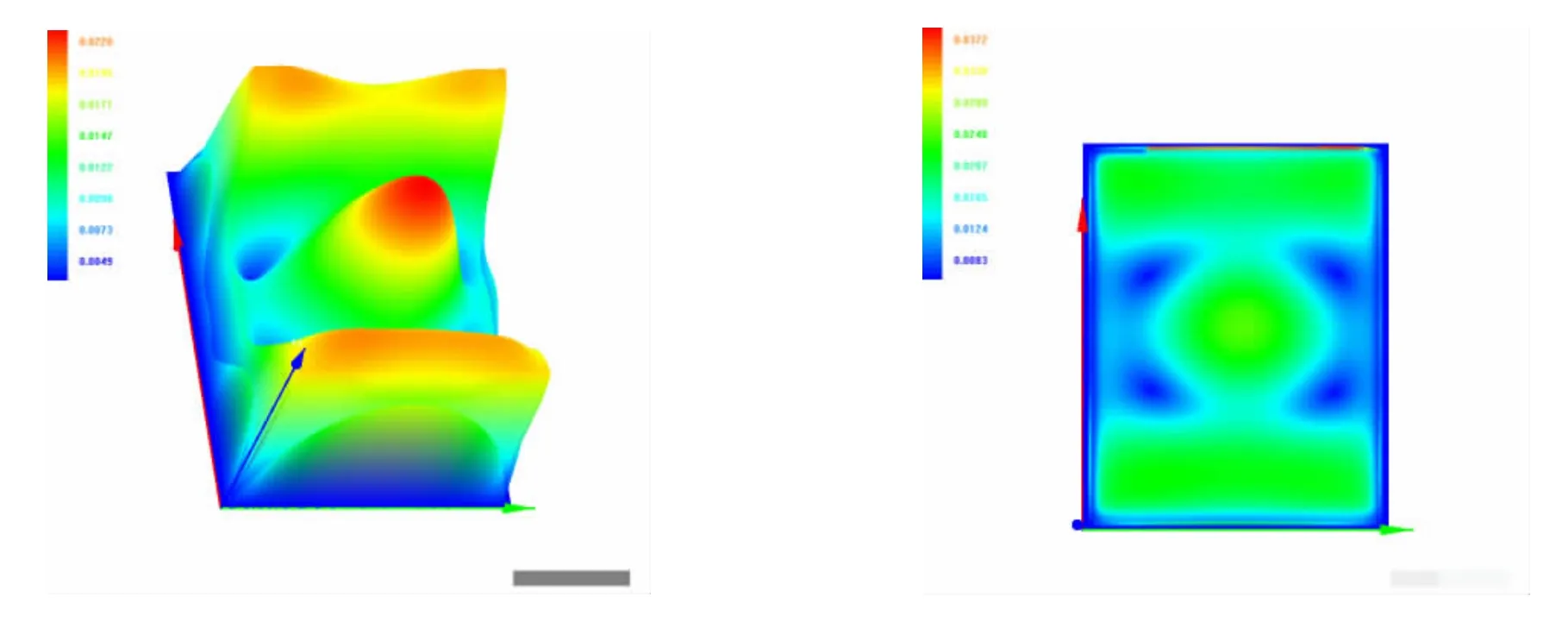
图9 腔体内的电磁场分布情况时域仿真

2）FDTD是整体迭代算法，即场的传播、散射和衰减等特性是靠整个空间的差分方程迭代获得的，每迭代一次，场传输半个网格长度，如果根据研究目标的复杂性划分为多个区域，每个区域有一个最优的FDTD算法适用，这样各个区域算法的连续性和场值传递的可靠性就需要加以考虑和解决。主要涉及到的是常规直角圆柱和球坐标系下的FDTD算法、曲线坐标系算法、细长物体对应的算法、细网格算法等，这些算法的连接和场值传递本身就是研究的重点。

3）GPU运算技术目前还存在亟待解决的问题。首先，GPU运算精度相比较CPU一般来说并没有太大优势，至多只是相当，其不同数学指令的运算精度也存在不同，因而它在执行诸如FDTD这样的迭代算法时，会出现误差累积的问题，尤其是针对三维问题，这一效应会更加明显。其次，GPU的流处理器一般只能处理二维数组，因而对于三维问题，其电磁场数据存储数组是三维、甚至是四维的，这时就必须进行数组转换，必然会增加核心计算程序的复杂度，频繁的数组转换也会影响程序效率同时也增加应用难度。而且，由于GPU的显存大小有限，在GPU上进行电大尺寸问题的运算也还是不可能的。

5 结 语

概述了时域有限差分法（FDTD）的一些发展情况，可以作为复杂形体瞬态电磁场分析的核心算法之一，针对并行计算、结合GPU运算、FDTD建模技术、网格剖分技术展开说明，给出一些实例和实现过程；并给出了雷电冲击下的物体周围电磁场分布、等离子体腔体内部电磁场分布等结果。可以看出完全符合瞬态电磁场的分析要求，最后还给出一些FDTD算法现在还未完全解决的、有待进一步研究的关键技术。

［1］ 高本庆．时域有限差分法［M］．北京：国防工业出版社，1995．

［2］ 薛正辉．电磁场的时域技术及应用［D］．北京：北京理工大学，2002．

［3］ JOHN D，O MIKE H，DAVID L，et al．GPU Computing［J］．Proceedings of the IEEE，2008，96（5）：1－18．

［4］ SEAN E K，LAURENCE E T，MICHAL M Q．Acceleration of finite－difference time－domain（FDTD）using graphics processor units（GPU）［A］．2004 IEE MTTS Digest［C］．［S．l．］：［s．n．］，2004．1 033－1 036．

［5］ TOMASZ P S，TIMOTHY D D．Acceleration of the 3D ADI－FDTD method using graphics processor units［A］．2009 IEEE MTT－S International Microwave Symposium Digest（MTT）［C］．［S．l．］：［s．n．］，2009．241－245．

［6］ PRICE D K，HUMPHREY J R，KELMELIS E J．GPU－based accelerated 2D and 3D f DTD solvers［A］．Physics and Simulation of Optoelectronic Devices XV［C］．CA：San Jose，2007．

［7］ 李蔚清，苏智勇，杨正龙，等．一种基于GPU的复杂目标电磁散射快速算法［J］．系统仿真学报，2006，18（8）：20－24．

［8］ 杨正龙，金 林，李蔚清．基于GPU的图形电磁计算加速算法［J］．电子学报，2007，35（6）：30－33．

［9］ 韩 林．基于GPU的光波导器件FDTD并行算法研究［D］．济南：山东大学，2007．

［10］ PENG Shao－xin，NIE Zai－ping．Acceleration of the method of moments calculations by using graphics processing units［J］．IEEE Transactions on Antennas and Propagation，2008，56（7）：2 130－2 133．

［11］ 刘 昆，王晓斌，廖 成．图形处理器（GPU）加速时域有限元的二维辐射计算［J］．电波科学学报，2008，23（1）：111－114．

O441

A

1008－1542（2011）12－0157－05

2011－06－20；责任编辑：张士莹

任 武（1976－），男，山西交城人，副研究员，博士，主要从事电磁兼容和计算电磁学方面的研究。