Banach空间中拟严格伪压缩映像族不动点的收敛定理

刘立红，陈东青，唐西南

（军械工程学院基础部，河北石家庄 050003）

Banach空间中拟严格伪压缩映像族不动点的收敛定理

刘立红，陈东青，唐西南

（军械工程学院基础部，河北石家庄 050003）

给出了Banach空间中拟严格伪压缩映像有限族公共不动点的迭代算法，并利用所给出的算法证明了一个强收敛定理，推广了近期的相关结果。

Banach空间；拟严格伪压缩映像；公共不动点；迭代算法

1 预备知识

设E为实Banach空间，E＊为E的对偶空间。正规对偶映像定义为

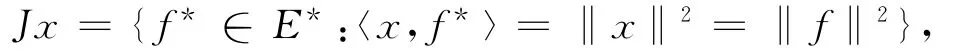
其中〈·，·〉表示广义对偶对。如果E＊是自反光滑的，则J是单值且半连续的。

设C是Hilbert空间H的非空闭凸子集，PC：H→C是从H到C的距离投影，则PC一定是非扩张的，但在Banach空间中结论不再成立。ALBER等在一般的Banach空间E中引入了广义投影算子ΠC：E→C，它是Hilbert空间中距离投影的一个类似［1］。

设E是自反的、光滑的、严格凸的Banach空间，考虑泛函

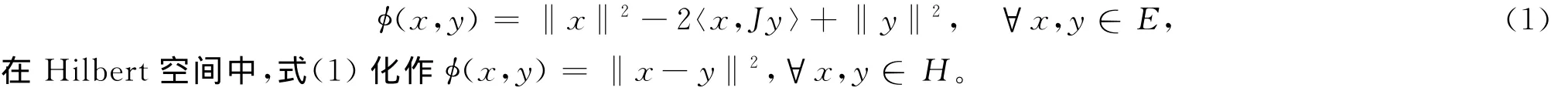
本文用F（T）＝｛x∈C｜Tx＝x｝表示映像T的不动点集，用

广义投影算子ΠC：E→C是一个映像，对每一个x∈E对应泛函φ（y，x）的最小值点，即ΠCx＝，其中是下面极小化问题的解：

根据φ（y，x）的性质和J的严格单调性可得φ（y，x）的最小值点的存在性和唯一性［2］。

在Hilbert空间中，ΠC＝PC。由φ的定义易得

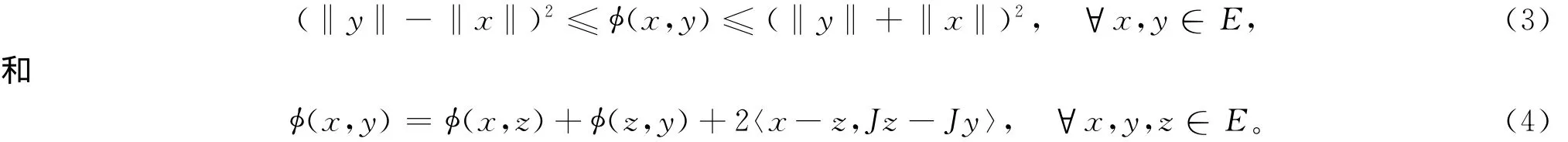
注1：若E是自反的、光滑的、严格凸的Banach空间，那么对于任意x，y∈E，φ（x，y）＝0当且仅当x＝y。

定义1［3］设C为Banach空间E中的非空闭凸子集，称映像T：C→C为拟严格伪压缩映像，若存在常数0≤k≤1，且F（T）≠Ø，如果对任意x ∈C及p∈F（T），恒有

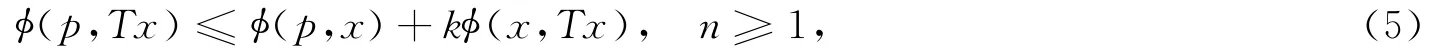
若k＝0，则称T为拟非扩张映像；若k＝1，则称T为拟伪压缩映像。

定义2［2］称Banach空间E具有K性质［1］，若对于任意序列｛xn｝⊂E，x∈E，如果

近期，ZHOU Hai－yun等在文献［4］中给出了自反的、严格凸的、且具有K性质的光滑Banach空间中拟严格伪压缩映像的不动点的迭代算法，本文将其推广至拟严格伪压缩映像的有限族的公共不动点情形，给出了相应的迭代算法，并证明了1个强收敛定理。

为证明本文主要结果，首先给出下述引理。

引理1［5］设E为自反的、严格凸的、光滑的Banach空间，C为E的非空闭凸子集，x∈E且x0∈C，则x0＝ΠCx当且仅当

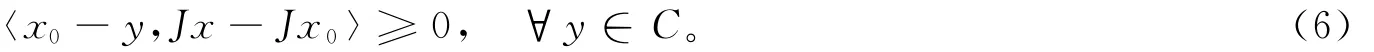
引理2［1］设E为自反的、严格凸的、光滑的Banach空间，C为E的非空闭凸子集，对任意x∈E，有

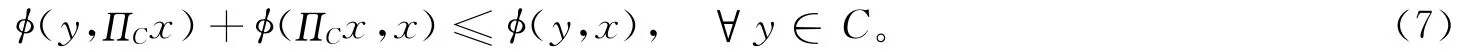
引理3［4］设E为自反的、严格凸的、光滑的Banach空间，C为E的非空闭凸子集，若映像T：C→C为闭的拟严格伪压缩映像，则F（T）是C的闭凸子集。

2 主要结果

定理 设E为自反的、严格凸的、光滑的Banach空间，E和E＊均具有K性质，C是E的非空闭凸子集，Ti：C→C（i＝1，2，…，N）为闭的拟－ki－严格为压缩映像有限族序列｛xn｝由下列迭代生成：

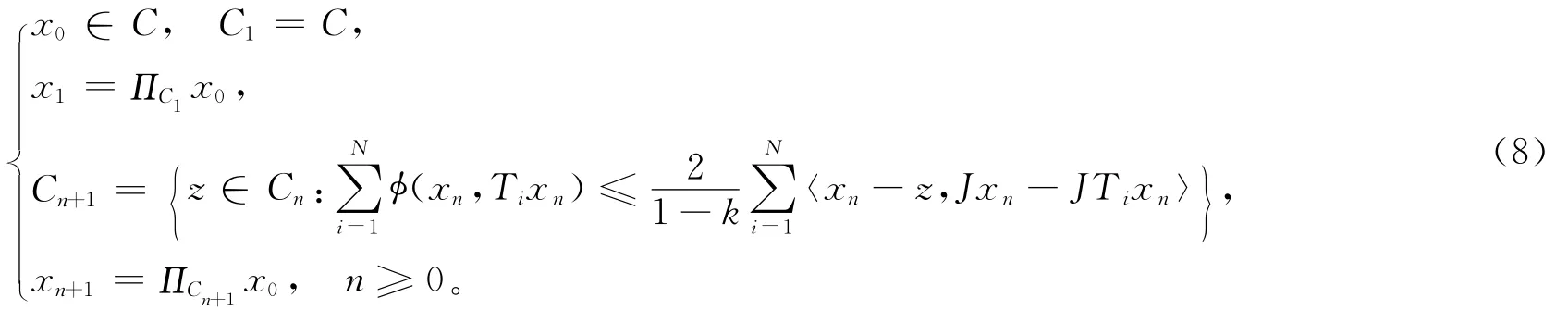
其中k＝max｛k1，k2，…，kN｝，则序列｛xn｝强收敛于ΠF（x0）。

证明 第1步：证明F和Cn均为闭凸集。

由引理3知F（Ti）（i＝1，2，…，N）为闭凸的，故也为闭凸的。下面证明Cn为闭凸的。

C1＝C为闭凸，设Ck为闭凸，z∈Ck＋1，则

第2步：证明F⊂Cn。

首先F⊂C＝C1。假设F⊂Ck，∀p′∈F⊂Ck，则由式（4）及式（5）可推得：

注2：定理将文献［4］中的拟严格伪压缩映像的不动点情形推广至拟严格伪压缩映像的有限族的公共不动点情形，给出了相应的迭代算法。

［1］ ALBER Y I，REICH S．An iterative method for solving a class of nonlinear operator equations in Banach spaces［J］．Panamer Math，1999，4：39－54．

［2］ HUDZIK H，KOWALEWSKI W，LEWICKI G．Approximative compactness and full rotundity in Musielak－orlicz spaces and Lorentz－orlicz spaces［J］．Z Anal Anwend，2006，25：163－192．

［3］ BAUSCHKE，COMBETTES P L．A weak－to－strong convergence principle for fejer－monotone methods in Hilbert spaces［J］．Mathematics of Operations Rresearch，2001，26：248－264．

［4］ ZHOU Hai－yun，GAO Xing－hui．An iterative method of fixed points for closed and quasi－strict pseudo－contractions in Banach spaces［J］．J Appl Math Comput，2010，33（1／2）：227－237．

［5］ ZHOU Hai－yun，GAO Gai－liang，TAN Bin．Convergence theorems of a modified hybrid algorithm for a family of quasi－asymptotically nonexpansive mappings［J］．J Appl Math Comput，2010，32（2）：453－464．

Convergence theorems of fixed points for family of quasi－strict pseudo－contractive mappings in Banach spaces

LIU Li－hong，CHEN Dong－qing，TANG Xi－nan
（Department of Basic Courses，Ordnance Engineering College，Shijiazhuang Hebei 050003，China）

This paper modifies the iterative algorithm of common fixed points for a finite family of quasi－strict pseudo－contractive mappings in Banach spaces．Then a strong convergence theorem is proved by the modified algorithm，which generalizes the recent results．

Banach space；quasi－strict pseudo－contractive mapping；common fixed point；iterative algorithm

O177．91

A

1008－1542（2011）06－0529－03

2011－04－22；责任编辑：张 军

国家自然科学基金资助项目（11071053）；军械工程学院基金项目（YJJXM11003）

刘立红（1972－），女，河北保定人，讲师，主要从事非线性泛函分析及其应用方面的研究。