Szász-Bézier和Baskakov-Bézier算子的加权逼近阶

刘国芬，禹长龙

（1.河北师范大学数学与信息科学学院，河北石家庄 050024；2.河北科技大学理学院，河北石家庄 050018）

Szász-Bézier和Baskakov-Bézier算子的加权逼近阶

刘国芬1，禹长龙2

（1.河北师范大学数学与信息科学学院，河北石家庄 050024；2.河北科技大学理学院，河北石家庄 050018）

利用一阶加权光滑模ωφλ（f，t）w讨论了 Szász-Bézier算子和 Baskakov-Bézier算子带权w（x）＝x a（1－x）b（0＜a＜1，b＞0）的点态逼近，并给出了它们的逼近阶。

Szász-Bézier算子和Baskakov-Bézier算子；光滑模；K-泛函；逼近阶

Bézier型算子［1］被引入之后，很多文献对这类算子进行了大量的讨论［2－6］。笔者也曾在文献［2］与文献［3］中给出了一些相关结论，完善了这方面的内容。对于加权逼近，在文献［7］－文献［9］中都有讨论，尤其是文献［7］中，给出了大量加权逼近的结论。而对于Bézier型算子的加权逼近，由于这类算子形式上的复杂性，未见有关方面的结果。笔者将利用一阶加权光滑模ωφλ（f，t）w给出Szász-Bézier算子和Baskakov-Bézier算子的点态加权逼近阶。

这2种算子统一形式的定义为

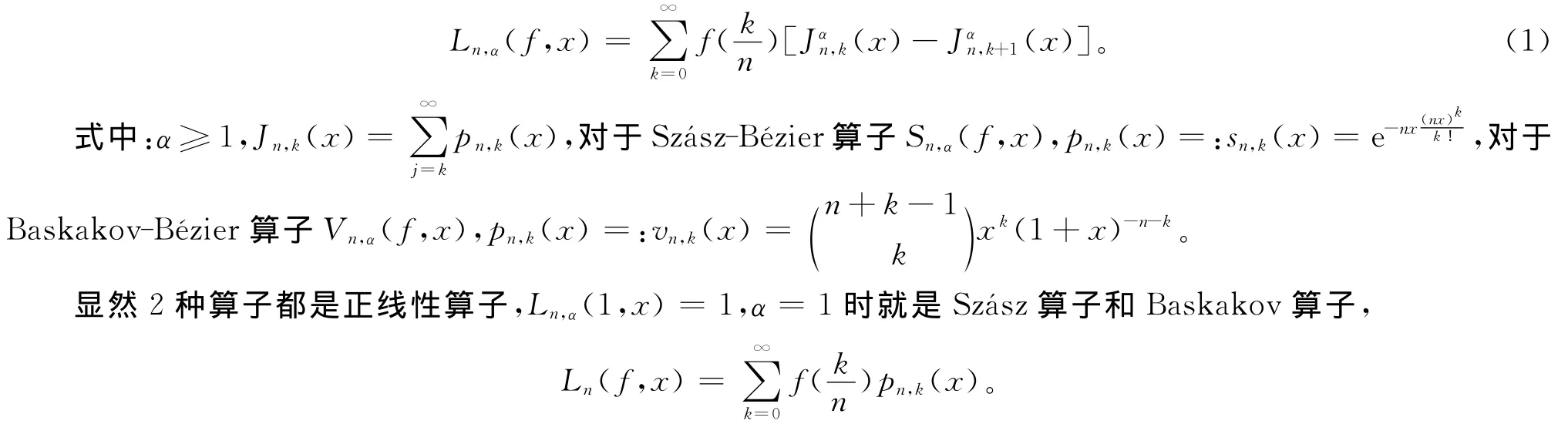
［1］CHANG Geng-zhe.Generalized Bernstein-Bézier polynomial［J］.J Comput Math，1983，（1）4：322-327.

［2］GUO Shun-sheng，QI Qiu-lan，LIU Guo-fen.The central approximation theorem for Baskakov-Bézier operators［J］.J Approx Theory，2007，147（1）：112-124.

［3］郭顺生，刘国芬.关于Szász-Durrmeyer-Bézier算子的点态逼近［J］.工程数学学报（Chinese Journal of Engineering Mathematics），2008，25（1）：81-89.

［4］ZENG Xiao-ming.On the rate of the convergence of the generalized Szász type operators for functions of bounded variation［J］.J Math Anal Appl，1998，226（2）：309-325.

［5］ZENG Xiao-ming，CHEN Wen-zhong.On the rate of convergence of the generalized Durrmeyer type operators for functions of bounded variation［J］.J Approx Theory，2000，102（1）：1-12.

［6］ZENG Xiao-ming，PIRIOU A.On the rate of convergence of two Bernstein-Bézier type operators for bounded variation functions［J］.J Approx Theory，1998，95（3）：369-387.

［7］DITZIAN Z，TOTIK V.Moduli of Smoothness［M］.New York：Springer-Verlag，1987.

［8］ZHOU Ding-xuan.Weighted approximation by Szász-Mirakjan operations［J］.J Approx Theory，1994，76（3）：393-402.

［9］宣培才，周定轩.Baskakov算子加权逼近的收敛阶［J］.应用数学学报（Acta Mathematicae Applicatae Sinica），1995，18（1）：129-139.

Pointwise weighted approximation by degree of Szász-Bézier and Baskakov-Bézier operators

LIU Guo-fen1，YU Chang-long2
（1.College of Mathematics and Information Science，Hebei Normal University，Shijiazhuang Hebei 050024，China；2.College of Sciences，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

By using one-order weighted modulus，we got approximation degree of Szász-Bézier and Baskakov-Bézier operators with weightw（x）＝x a（1－x）b（0＜a＜1，b＞0）.

Szász-Bézier and Baskakov-Bézier operators；modulus of smoothness；K-functional；approximation degree

O174.41

A

1008-1542（2011）06-0532-04

2011-06-29；责任编辑：张 军

国家自然科学基金资助项目（10801043）

刘国芬（1974-），男，河北高阳人，讲师，博士，主要从事函数逼近论方面的研究。