摆角、摆长及周期数对测重力加速度的影响分析

翟凤瑞, 李宇赤，易中周, 张黎黎, 王 丹

（1.红河学院 理学院，云南 蒙自 661100；2.西双版纳职业技术学院，云南 景洪 666100）

摆角、摆长及周期数对测重力加速度的影响分析

翟凤瑞1, 李宇赤2，易中周1, 张黎黎1, 王 丹1

（1.红河学院 理学院，云南 蒙自 661100；2.西双版纳职业技术学院，云南 景洪 666100）

用单摆法测量重力加速度是普通物理实验中常用的方法，但在实验中，摆角、摆长和周期数常常对重力加速度的测量误差产生一定的影响.文章主要分析不同摆角、摆长及周期数三个条件对测重力加速度的影响,最终由处理分析结果可知，在普通物理实验室里，取摆角、摆长＝47或55cm、周期数 次，处理得到的重力加速度与本地的理论计算值很接近.

摆角；摆长；周期数；重力加速度

引言

地球对物体的万有引力称为重力，物体在重力作用下具有的加速度称为重力加速度.重力加速度的数值，随地理纬度和相对于海平面的高度不同而略有差异.一般说来，在赤道附近重力加速度的数值最小，越靠近南、北两极，重力加速度的数值越大[1].重力加速度的测量方法有很多种，它们各有特点.其中单摆法装置简单, 测量手段便捷, 在普通物理学实验教学中应用比较普及,也比较重要，而用此种测量方法来测重力加速度，其测量结果的精确性直接受到摆角、摆长及周期的影响，不同的测量条件将对重力加速度的测定产生不同的误差[2].所以本文主要分析研究不同条件对用单摆法测重力加速度的影响，并最终确定一组适合本地测重力加速度的最佳测量条件，在实验教学方面有重要意义.

1 实验主要仪器

单摆法测重力加速度的实验仪器见下表1：

表1 实验仪器

2 实验数据处理及分析

2.1 本地重力加速度值

根据蒙自的地理位置：经度：103°23′东，纬度：23°23′北，海拔：1302m，根据地球任意地方重力加速度的计算公式可得到蒙自本地重力加速度理论计算值为[3]：

2.2 不同摆角对重力加速度的影响

在温度为22.0℃、湿度为22.4℃的条件下，实验过程中固定摆长为40㎝，周期数取值为40次，用单摆三线摆组合仪、自由落体仪上安装单摆装置，改变摆角6次，各测量结果及数据处理见下表2、表3.

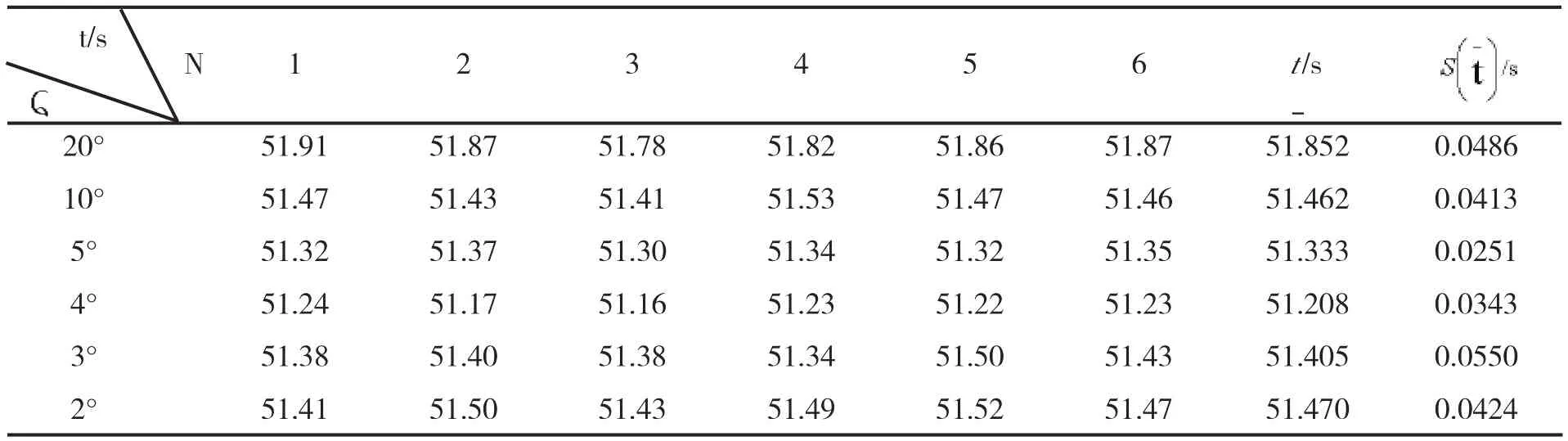
表2 不同摆角下的测量数据及处理

表3 不同摆角条件下的重力加速度值

综合上述各摆角的重力加速度的测试结果，可得重力加速度与摆角之间的变化关系如下图1所示.

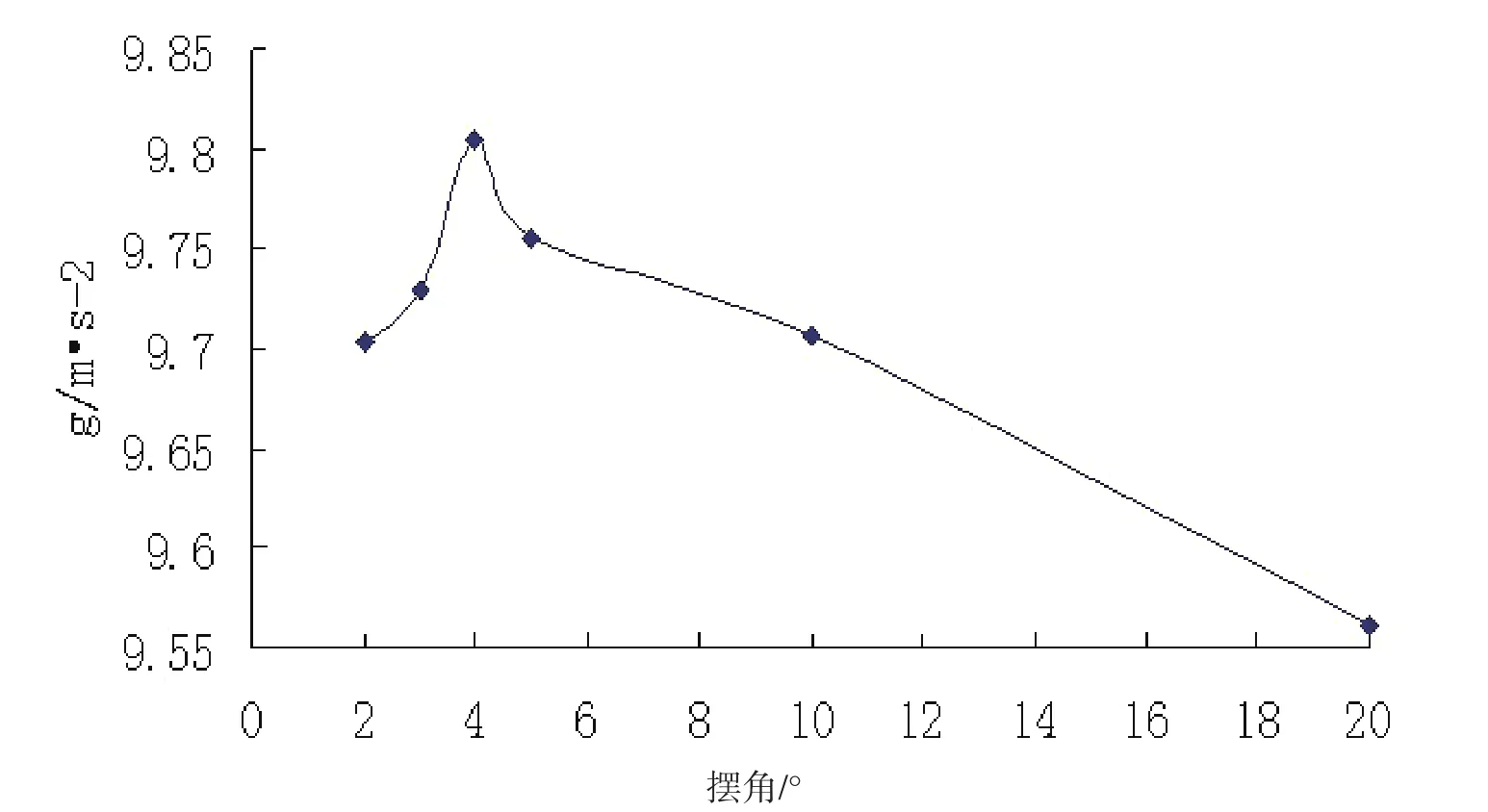
图1 重力加速度与摆角的关系

普通物理学中认为，单摆在小角度的振幅( 时)可以看成简谐振动，用实验的方法可以求出其振动的摆长与周期，进而可以测得重力加速度.但在实验中不是摆角越小测量值越精确，当摆角很小时，操作引入的误差增长更快.当单摆的角振幅较大时,单摆的运动和简谐振动的差异增大，对测重力加速度产生的误差增大，同时摆长的长短也将对重力加速度的测定带来误差.从图1可知，在 为4°附近出现极值，并且越往两端走重力加速度的值变化越大，其原因主要为：第一，当摆角增大时，摆球的速度随之增大，此时空气阻力已不可忽略；第二，当 增大时，计算公式中的高阶项已不能省去；第三，摆角很小时动手操作反应误差随之增大.对照本地重力加速度的理论计算值可知，摆角一般选3.8°左右为最佳.

2.3 不同摆长对重力加速度的影响

在室温为22.0℃、湿度为22.4℃的条件下，实验过程中的摆角定为4°，周期数为40次，共改变摆长7次，各测量数据结果及处理见表4，不同摆长条件下测量计算出的重力加速度见下表5：

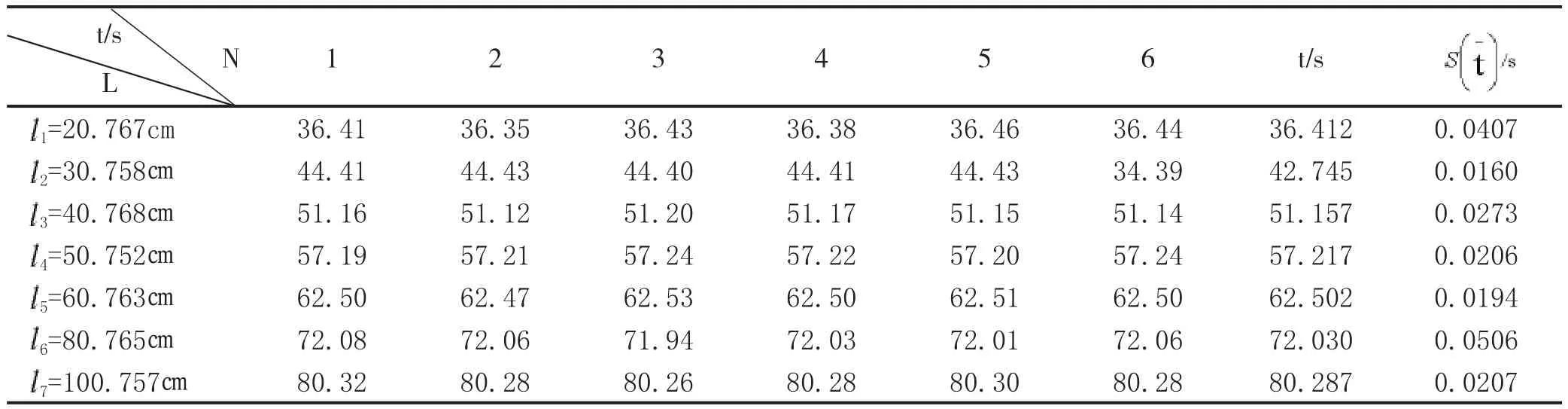
表4 不同摆长下的测量数据及处理

表5 不同摆长条件下的重力加速度

由表5结果可得重力加速度与摆长之间的变化关系下如图2所示：

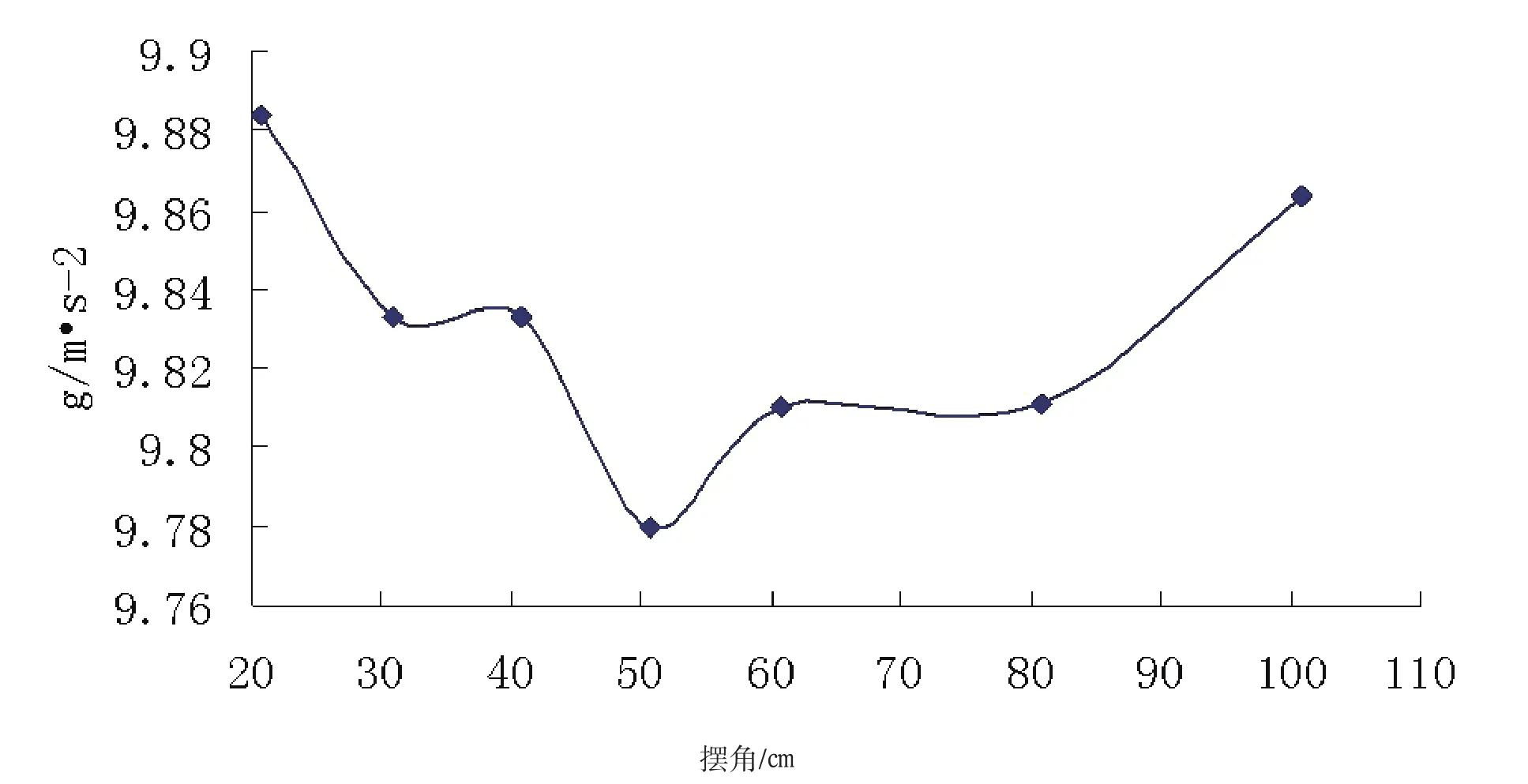
图2 重力加速度与摆长的关系

在研究单摆周期与摆长关系时，摆长的取值受小球半径的约束，它们之间的关系[4]是也就是的实验中“依次缩短摆长”5次，所取摆长L必须满足实际上L取值并非越大越好，因为L太大实验条件不允许，空气阻力也会变大，而且L的增大将会引起由于细线质量不能忽略出现的误差.从图2中可知：当摆长在45-55㎝之间变化时，引起的重力加速度改变很小，接近于本地重力加速度值，但越往两端走，其重力加速度值偏离越明显，在实验中，由于实验器材的限制，摆长不能过长，而过短则有小球的半径约束，对照本地重力加速度值，在普通实验室里一般取为47㎝或55㎝.这样可以使在普通物理实验中测量值更接近真实值.

2.4 不同周期数对重力加速度的影响

在温度为22.0℃、湿度为22.4℃的条件下，取摆角为4°，摆线长为50㎝，用螺旋测微计测球的直径d（小球不变），改变周期数 次所用的时间为 ，各测量结果及数据处理见下表6和表7：

表6 对不同周期数的测量数据处理

表7 对不同周期数重力加速度的值

由表7计算结果可得重力加速度与周期数之间的关系如下图3：

图3 周期数与重力加速度的关系

对于周期数的误差主要来源不仅决定于秒表的精度，还决定于人的反应时间.人从摆球第一次经过平衡位置时按表开始，到最后一次摆球经过平衡位置时按表结束，两次都存在反应时间.实验中用停表计时，无论是机械停表，还是电子停表，应从计时绝对误差来考虑，而不能单一从停表的最小分度值来考虑.计时绝对误差主要由表的走时误差、测量者对摆球到达平衡位置时刻的判断、测试看的反应时间、停表的操作熟练程度和停表的启动和制动性能诸多因素共同决定.从图3可知：随着周期数n的增加出现一个过渡阶段，周期的误差主要来源不仅决定于秒表的精度和决定于人的反应时间，而周期数越少误差比例越大，但周期数也不能无限的增大，从实验过程中可知道，由于空气阻力的存在，在经过多次摆动后摆幅明显减小，随之引入的误差增大.对照本地重力加速度计算值，在实验室里周期数一般可选取37次.

3 结论

综上对摆角、摆长及周期数对测量重力加速度的影响分析可以看出，摆角、摆长及周期数对重力加速度的测量都有很大的影响，摆角越大所产生的误差也就越大，摆长过大或太小对测量结果的影响也比较大，周期数太大由于空气阻力的影响就大.根据蒙自本地重力加速度理论计算值的比较结果知，取摆角 、摆长 cm、周期数 次时，测试结果与本地重力加速度的理论值非常很接近.

[1] 杨述武.普通物理实验(力热部分)第三版[M].北京：高等教育出版社,2005:69-111．

[2] 曾腾.用不确定度分析单摆的摆角与摆长对测重力加速度的影响[J].物理教学探讨,2 0 0 6,2 4(3):33-34

[3] 姜向东,杨士君等.大学物理实验[M].成都：西南交通大学出版社，2006:23-56.

[4] 郑立.单摆实验中摆长的讨论[J].黄山学院学报,2006,8(3):39-40．

Influence and Analysis of Pendulum Angle, Pendulum Length and Periodicity on the Acceleration of Gravity

ZHAI Feng-rui1, LI Yu-chi2,YI Zhong-zhou1, ZHANG Li-li1, WANG Dan1
(1.College of Science, Honghe University, Mengzi 661100, China;2.Xishuangbanna Vocational and Technical Institute,Jinghong 666100,China)

It is an ordinary method to measure acceleration of gravity with a pendulum in physical experiments.But in the experiment,the pendulum angle, pendulum length and periodicity often have some influences on measurement errors of acceleration of gravity.This paper mainly analyzes the influences of pendulum angle, pendulum length and periodicity on the acceleration of gravity.It can be seen from the processing and analysis results that the value of acceleration of gravity by experiments is very close to the local acceleration theoretical value when the swing angle is 3.8 degrees, pendulum length is 47 cm or 55 cm and periodicity is 37 times.

pendulum angle; pendulum length; periodicity; acceleration of gravity

O4-3

A

1008-9128（2011）04-0019-04

2011-06-02

云南省教育厅科学研究基金资助项目（6y0038D）；红河学院基金资助项目（XJ1Y0807）

翟凤瑞（1978-），男，讲师，硕士.研究方向：绿色复合材料及无机非金属材料的研究.

[责任编辑 张灿邦]