一种特征值隔离的规则化方法以及特征值估计的改进研究

李 杰,齐晓慧

(军械工程学院光学与电子工程系,河北石家庄 050003)

一种特征值隔离的规则化方法以及特征值估计的改进研究

李 杰,齐晓慧

(军械工程学院光学与电子工程系,河北石家庄 050003)

估计特征值的分布和大小,不仅在理论上十分重要,而且具有实用价值。本文基于Gerschgorin定理,提出了一种利用相似变换进行特征值隔离的规则化方法,给出了特征值能隔离的充要条件,克服了以往方法不具有通用性或者应用较为复杂的缺点。在研究了特征值隔离的规则化方法基础上,进一步提出了利用非线性规划改进特征值估计的方法,使特征值大小估计更为准确。

Gerschgorin定理;特征值隔离;特征值估计;相似变换;非线性规划

估计特征值的分布和大小,不仅在理论上十分重要,而且具有实用价值。如自动控制研究控制系统稳定性,需确定系统特征值是否均具有负实部;又如,在用迭代法求解线性方程时,为讨论其收敛性,需要估计迭代矩阵的谱半径是否小于1;再如,在判断方阵的幂级数是否收敛也要看方阵的特征值的模是否小于某一正实数。对特征值分布和大小的估计已有不少结果,其中最基本的定理是著名的 Gerschgorin定理[1]。

但是,直接应用Gerschgo rin定理有两个缺点:一是只能得到n阶矩阵的特征值被包含在复平面上的n个圆盘的并集内,而不能得到单个特征值所在的区域;二是所得的区域过大,较为粗略。为解决前一个问题,需进行特征值隔离。通常的做法有区域分析法和相似变换法(两者还可以结合列圆盘)[2]。但前者过于复杂,不具通用性;而后者停留在试凑阶段,在构造对角矩阵D=diag(α1,α2,…,αn)对特征值隔离时,并没有一种规则化的方法,而且对矩阵能否隔离也未给出严格的论证和完整的说明。为解决后一个问题,需改进特征值估计。这方面已经有不少研究成果[3-7]。

本文基于Gerschgorin定理,提出了一种利用相似变换进行特征值隔离的规则化方法,给出了特征值能隔离的充要条件,克服了以往方法不具有通用性或者应用较为复杂的缺点。在研究了特征值隔离的规则化方法基础上,进一步提出了利用非线性规划改进特征值估计的方法,使特征值大小估计更为准确。

1 Gerschgo rin定理简介及相似变换应用于特征值隔离存在的问题

1.1 Gerschgorin定理简介

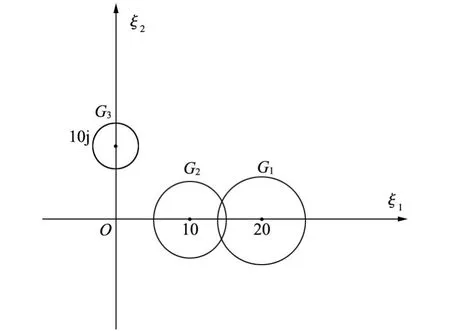
图1

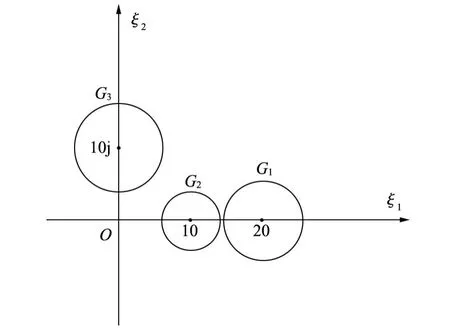
图2

对于例1,可以用试凑的方法得到对角矩阵D,简单易行。考虑如下矩阵:

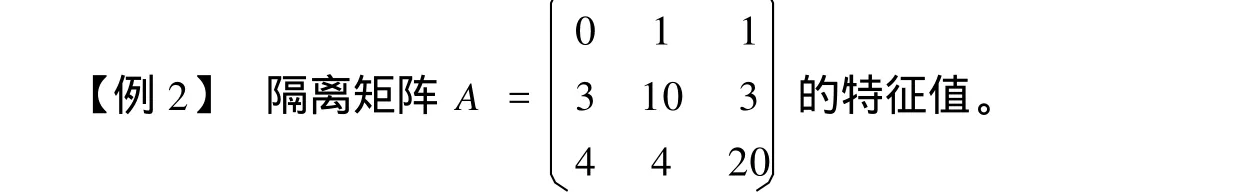
对于例2,可以验证,当α1=1,α2∈(0.23 0.49),α3∈(0.34 0.38),或α1=1,α2∈(0.28 0.42),α3∈(0.33 0.43),特征值是可以隔离的。但是在这样一个范围取值,用试凑的方法显然很难得到。

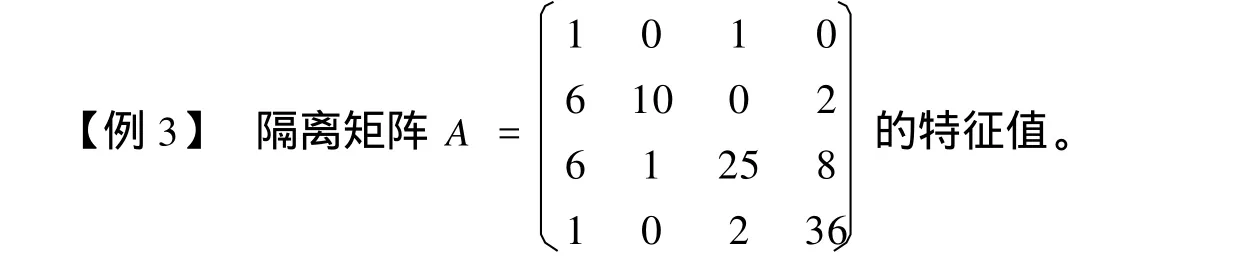
对该四阶矩阵,用试凑法隔离特征值同样是有难度的。当矩阵为五阶、六阶或者更高阶的时候,试凑显然不适用。有没有一种规则化方法能确定对角矩阵各元素范围使特征值隔离?

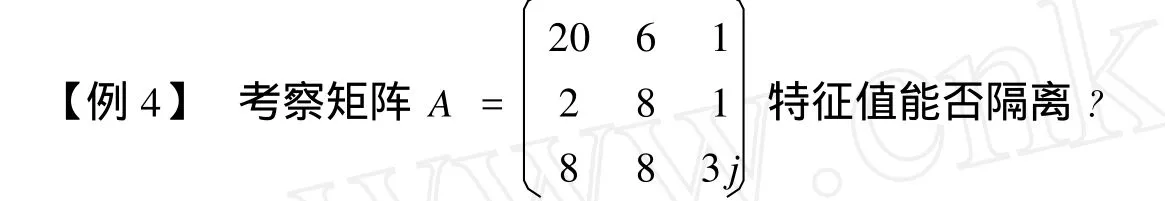
对于例4,找不出一个对角矩阵使得特征值隔离。那么,特征值能进行隔离的充要条件是什么?

通过例2、例3和例4可知,用试凑法进行特征值隔离具有其局限性及缺点,表现在不适用于难以试凑、阶数较高的矩阵以及不能对特征值能否隔离进行判断。基此,提出隔离的规则化方法以及能隔离的充要条件,有效地解决了上述问题。

2 特征值隔离规则化方法及算例

下面以三阶矩阵为例,给出特征值隔离的规则化方法。

推广:对A=(aij)n×n,构造对角矩阵D=diag(α1,α2,…,αn),其中α1=1,α2,…,αn均为正数,根据两圆没有公共部分,其半径之和必小于两圆心距离,利用上述性质,可构造相应的C2n个不等式,满足不等式的解必能使特征值隔离。

显然,若矩阵能隔离,则特征值互异且主对角线上不含相同元素。顺便指出,若行圆盘不能隔离,可以尝试用列圆盘。

根据上述规则化方法,可得如下定理:

【定理】 对A=(aij)n×n,特征值能隔离的充要条件为构造的相应C2n个不等式有解;满足不等式的解的范围内任意取值,可使特征值隔离。

特征值要隔离,则盖尔圆不能相交或相互包含,进而满足其半径之和必小于两圆心距离,即满足相应的不等式,故定理的成立是显然的。

3 改进特征值估计的方法

在研究了特征值隔离的规则化方法基础上,利用非线性规划,可以对特征值估计的结果加以改进。利用对角变换进行特征值隔离的本质是对不同的圆分别进行相应的扩大或者缩小,从而实现不同的圆相互隔离。利用这一点,可以考虑单独一个圆与剩下其他圆的关系,使这个圆半径尽量小,同时不与剩下的其他圆相交或包含,这个圆所对应的特征值则确定在的一个较小的区域内;依次可以把每个圆所对应的特征值范围进行缩小,进而实现了对特征值估计的改进。这种思路按特征值能否隔离,又可分两种情况讨论。

推广:对A=(aij)n×n,构造对角矩阵D=diag(α1,α2,…,αn),其中α1=1,α2,…,αn均为正数,在构造的个不等式中按上述思路分别取定n-1个不等式以及相应的目标函数,依次求得每个特征值所在的较小圆盘区域,改进特征值估计的结果。

情况2:特征值不能完全隔离,退而求其次,尽可能得到更精确的特征值范围。考虑例3,构造如下不等式:

得到λ2更精确的范围;不存在,即不能同时与另外两圆分离,此时可以仍用原来的(即未经相似变换)盖尔圆作为r3的估计。虽然上述思路和能隔离情况是一样的,但考虑到某些情况下(如此例),构造的每一组不等式不一定有解,即不一定每一个圆都能与其他圆分离,此时,尽可能得到能孤立的特征值的精确范围,一定程度上改进了特征值估计的结果。

同理,可以适用于任意阶矩阵的情形。

4 结束语

试凑法构造对角矩阵进行相似变换简单但有其局限性。本文结合不等式,利用Lingo软件给出了构造对角矩阵隔离特征值的规则化方法以及特征值能隔离的充要条件,并利用非线性规划对特征值大小估计的结果加以改进。实例证明,本文有其一定的应用价值。结合不等式的思路能否在广义特征值、奇异值的估计中加以运用还有待进一步研究。

[1] 徐仲,张凯院,陆全等.矩阵论简明教程[M].北京:科学出版社,2001.

[2] 张凯院,徐仲.矩阵论辅导教案[M].西安:西北工业大学出版社,2007,3版.

[3] 张玉海,朱本仁.关于对称矩阵特征值的估计[J].高等学控计算数学学报,l993,3:(287-290).

[4] 沈光星,陈娅红,卢诚波.Gerschgorin定理的推广[J].丽水师范专科学校学报,2002,(24):1-3.

[5] 沙吾提·阿吾提.关于矩阵特征值的估计方法[J].新疆大学学报(自然科学版),2008,(29):14-18.

[6] 堕枣匮,赵金中.对称矩阵特征值估计的某些进展[J].天津理工学院学报,1992,(2):1-7.

[7] 陈筠青,张镭藩,单锋.探讨矩阵特征值的估计和定位[J].沈阳航空工业学院学报,1998,(15):41-45.

An inerratic method of eigenvalue isolation and research of amelioration of eigenvalue estimate

LIJie,QIXiao-hui

(Department of Optics and Electronics Engineering,Ordnance Engineering College,Shijiazhuang Hebei050003,China)

Estimating the distribution and size of Eigenvalue is very important in theory,and it also has p ractical value.In the paper,a inerratic method of eigenvalue isolation w ith sem blable transfo rmation is p roposed based on Gerschgorin theorem,and the sufficient and necessary conditions of eigenvalue possibly insulated are brought fo rw ard,w hich overcomes fo repassed methods’defects that they aren’t universal or relative comp licated for app lication.Based on the above research of inerraticmethod of eigenvalue isolation,a method of amelio rate eigenvalue estimate w ith nonlinear p rogramm ing is p roposed,w hich makes it more exact to estimate the size of eigenvalue.

Gersichgo rin theo rem;Eigenvalue isolation;Eigenvalue estimate;Sem blable transfo rmation;Nonlinear p rogramming

O241

:A

1001-9383(2011)02-0005-05

2011-02-20

李 杰(1988-),男,湖南省娄底市人,硕士研究生,主要从事复杂系统控制理论及应用.