Ψ-bounded Solutions for a System of Di ff erence Equations on Z∗

HAN YU-LIANG,LIU BAI-FENG AND SUN XI-DONG

(College of Mathematics and Information Scieces,Shandong Institute of Business and Technology,Yantai,Shandong,264005)

Ψ-bounded Solutions for a System of Di ff erence Equations on Z∗

HAN YU-LIANG,LIU BAI-FENG AND SUN XI-DONG

(College of Mathematics and Information Scieces,Shandong Institute of Business and Technology,Yantai,Shandong,264005)

In this work we discuss the existence of Ψ-bounded solutions for linear di ff erence equations.We present a necessary and sufficient condition for the existence of Ψ-bounded solutions for the linear nonhomogeneous di ff erence equation x(n+1)= A(n)x(n)+f(n)for every Ψ-bounded sequencef(n).

di ff erence equation,Ψ-bounded solution,existence

1 Introduction

The di ff erence equations play an important role in many scienti fi c fields,such as scienti fi c computing,numerical analysis of ordinary and partial differential equations,control theory and computer science(see[1]–[3]and references therein).The behavior of solutions of di ff erence equations has been paid much more attention by mathematicians and scientists, and the boundedness of solutions is closely related to the investigation of numerical discretization for differential equations(see[1],[2]and[4]).The boundedness of the solution of ordinary differential equations is a very important property.For example,the existence of the bounded solution implies the existence of the almost periodic solution(see[5]).

The problem of boundedness of the solutions for the system of ordinary differential equations

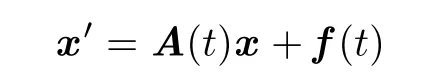
was studied by Coppel[6].Diamandescu[7],[8],[9]proposes the concept ofΨ-boundedness of solutions,which is interesting and useful in some practical cases for differential equations, and presents the existence condition for such solutions.Han[10]de fi nedΨ-boundedness ofsolutions for di ff erence equations

viaΨ-bounded sequences and established a necessary and sufficient condition for existence ofΨ-bounded solutions for everyΨ-summable sequence f on N.Diamandescu[11]gave a necessary and sufficient condition for the existence ofΨ-bounded solutions for the nonhomogeneous linear di ff erence equation(1.1)for everyΨ-summable sequence f on Z.

The aim of this paper is to give a necessary and sufficient condition for the nonhomogeneous system of ordinary di ff erence equations(1.1)to have at least one Ψ-bounded solution on Z for everyΨ-bounded sequence f on Z,where Z is the integer set.

Let Rdbe the Euclidean d-space,and

For a d×d matrixM,de fi ne the norm

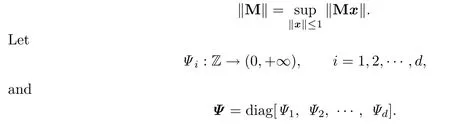
The matrix Ψ(n)is invertible for each n∈Z.

De fi nition 1.1A sequenceφ:Z→ Rdis said to beΨ-bounded onZifΨ(n)φ(n)is bounded onZ.

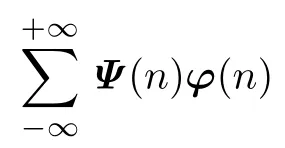
We assume that{A(n)}is a bounded matrix sequence and the associated linear di ff erence system is

Let Y be the fundamental matrix of(1.2)with Y(0)=Id,the identity d×d matrix.

Let the vector space Rdbe represented as a direct sum of three subspace X−,X0,X+such that a solution y(n)of(1.2)is Ψ-bounded on Z if and only if y(0)∈X0,and Ψ-bounded on Z+if and only ifand Ψ-bounded on Z−if and only ifAlso,let P−,P0,P+denote corresponding projection onto X−,X0,X+,respectively.

Lemma 1.1LetY(n)be an invertible matrix onZ+andPbe a projection.If there exists a sequenceφ:Z+→(0,+∞)and a positive constantMsuch that

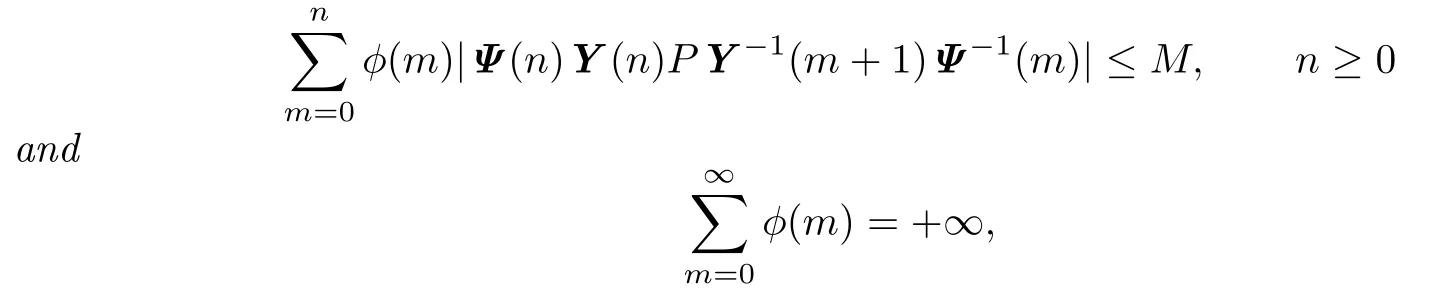
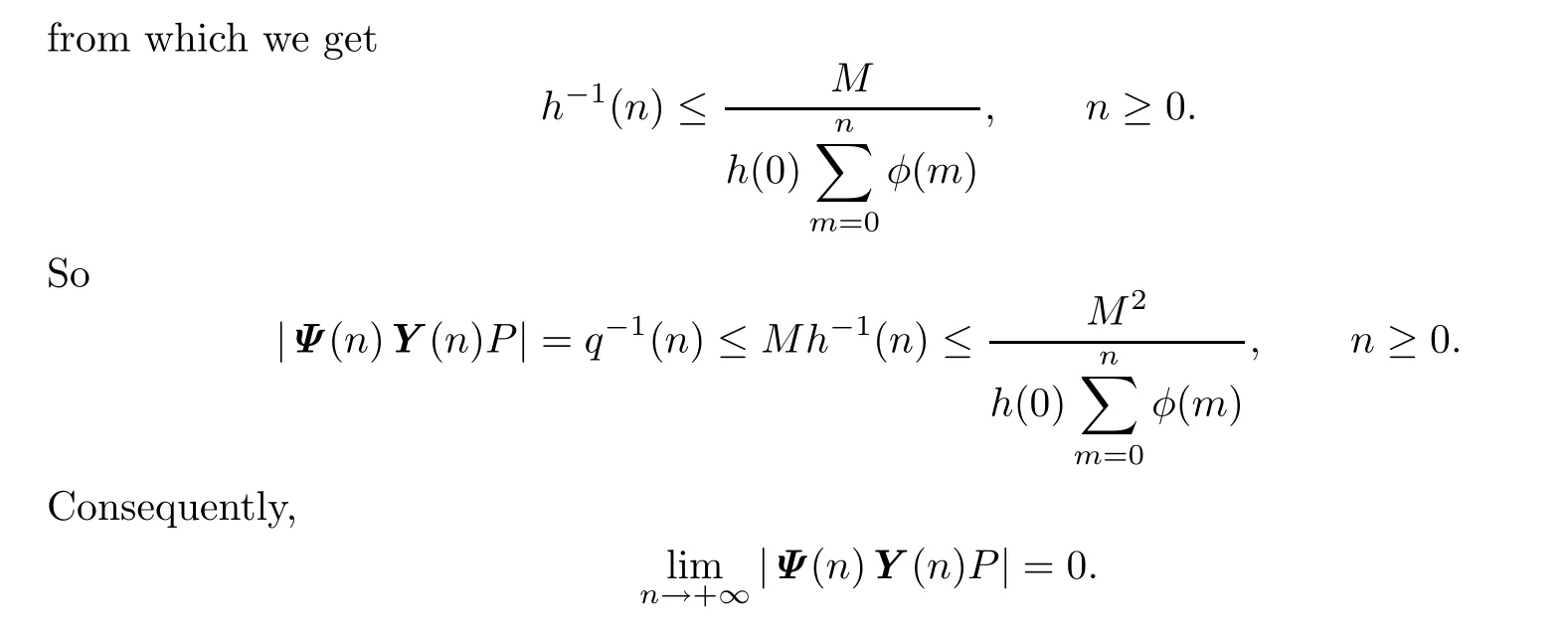
2 The Main Result

Theorem 2.1IfA(n)is a boundedd×dreal matrix sequence onZ,then the system(1.1)has at least oneΨ-bounded solution onZfor everyΨ-bounded sequencef:Z→Rdif and only if there exists a positive constantKsuch that

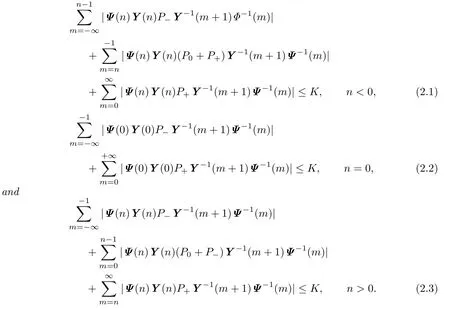
Proof.First,we prove the necessary part.

Suppose that the system(1.1)has at least one Ψ-bounded solution on Z for every Ψ-bounded sequence f:Z→Rdon Z.We denote by B the Banach space of all Ψ-bounded sequence x:Z→Rdwith the norm

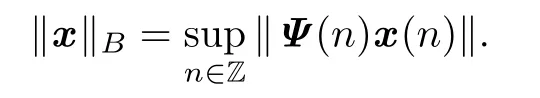
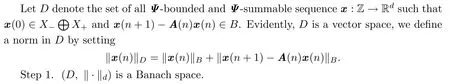
The proof is standard so we omit it.

Step 2.There exists a positive constant K0such that,for every f(n)∈B and for the corresponding solution x(n)∈D of(1.1),

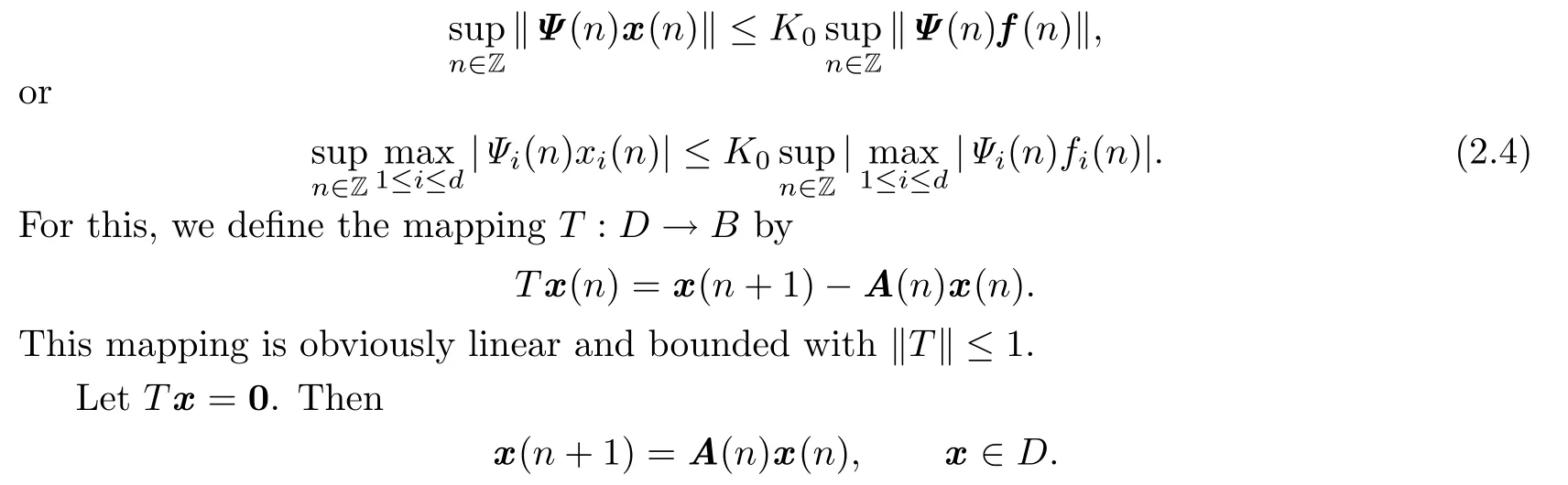
This shows that x(n)is a Ψ-bounded solution of(1.2).Then x(0)∈X0∩(X−⊕X+)={0}. Thus,x=0,so the mapping T is one-to-one.

Now let f∈B and x be the Ψ-bounded solution of the system(1.1).Let Z be the solution of the Cauchy problem

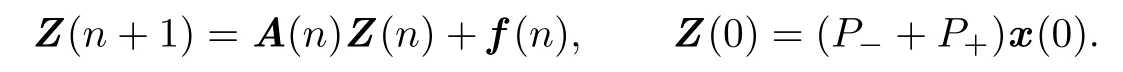
Then u=x−Z is a solution of(1.2)with

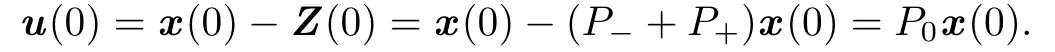
From the de fi nition of X0it follows that u is Ψ-bounded on Z.Thus,Z∈D and TZ=f. Consequently,the mapping T is onto.

From a fundamental result of S.Banach that if T is a bounded one-to-one linear operator of one Banach space onto another,then the inverse operator T−1is also bounded,we have

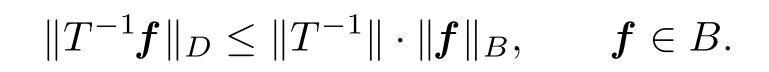
For a given f∈B,let x=T−1f be the corresponding solution x∈D of(1.1).We have

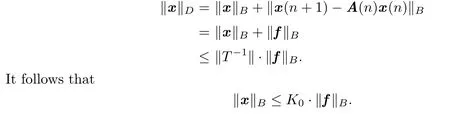
Step 3.The end of the proof.

Let T1＜0＜T2and T1,T2∈Z,f:Z→ Rd,a summable and Ψ-bounded sequence which vanish on Z−{T1+1,···,0,1,···,T2−1}.It is easy to see that the sequence x:Z→Rdde fi ned by

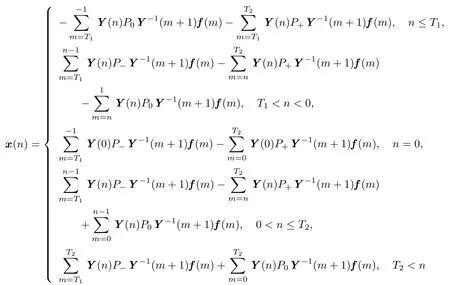
is the solution in D of the system(1.1).

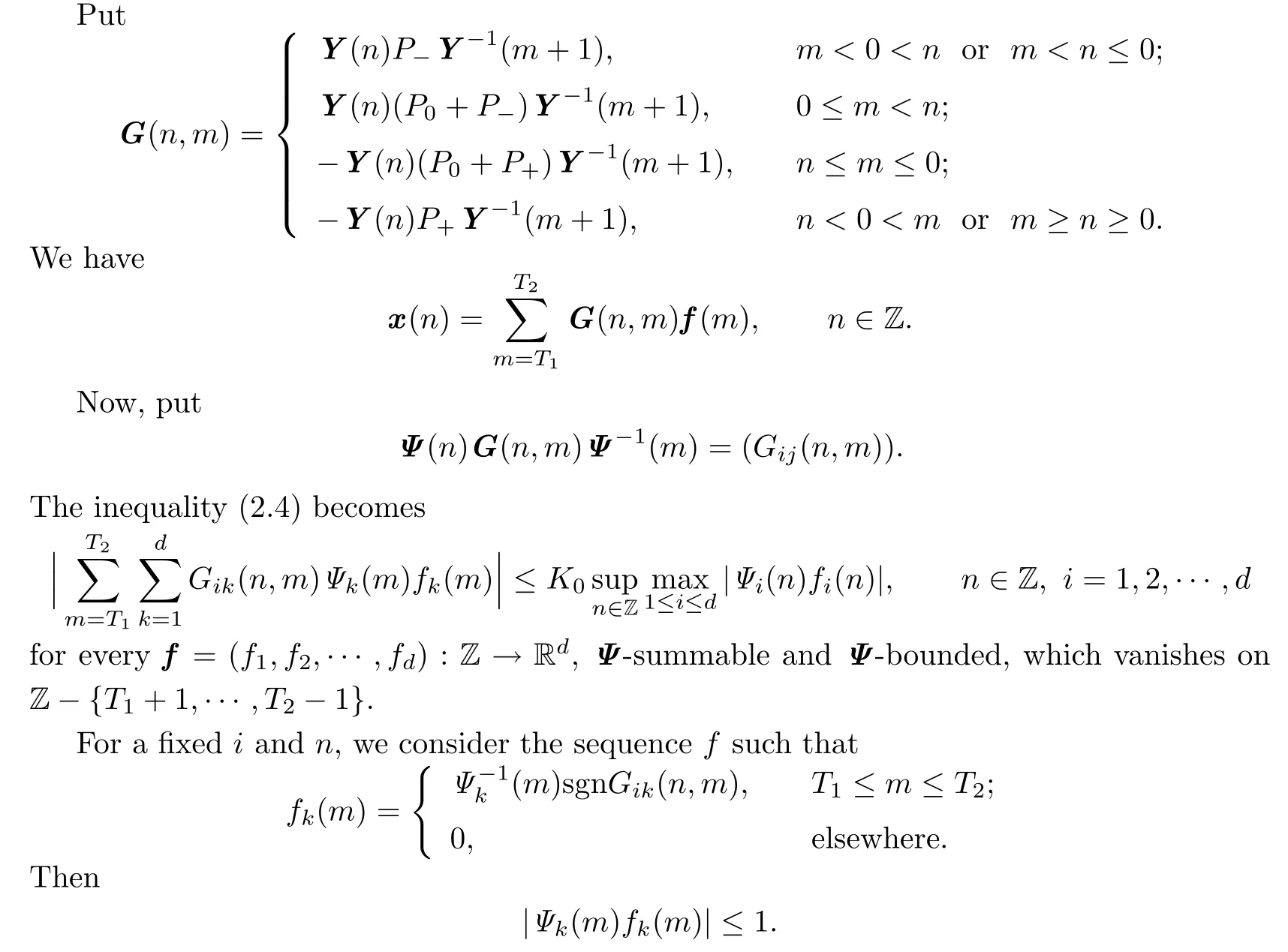
The above inequality holds for this sequence.

By the theorem of dominated convergence we get

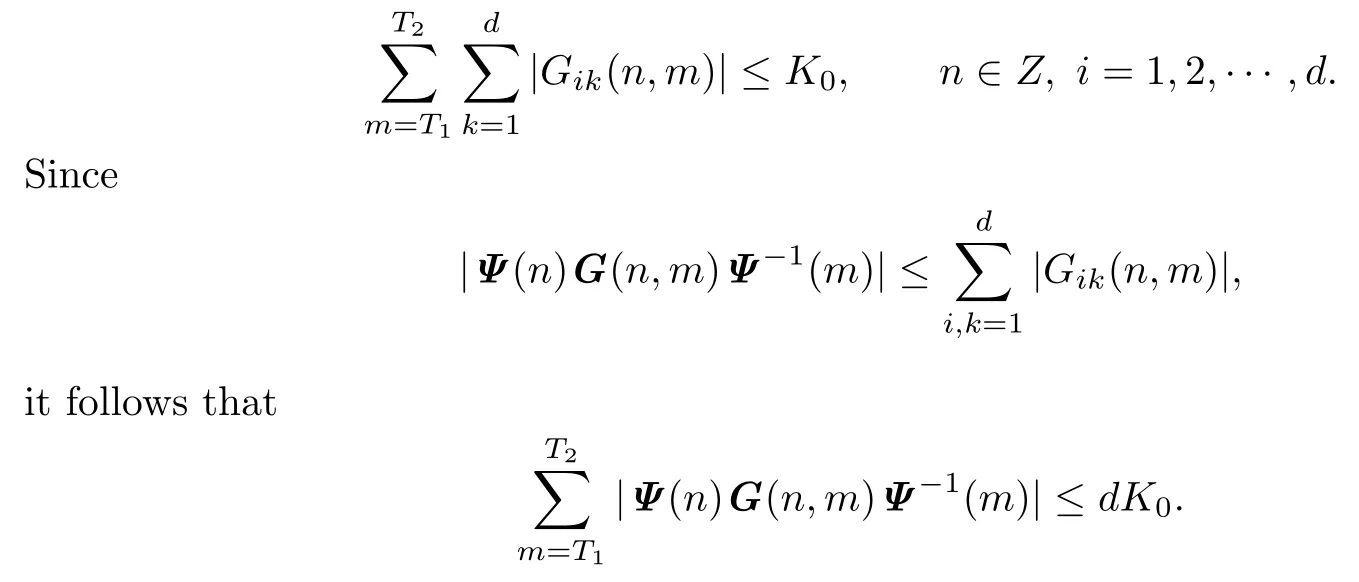
This holds for any T1＜0 and T2＞0.Hence|Ψ(n)G(n,m)Ψ−1(m)|is summable over Z and

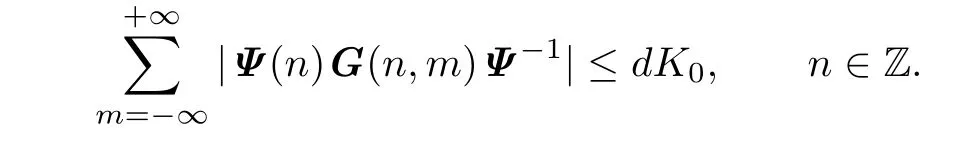
By the de fi nition of Ψ(n)G(n,m)Ψ−1(m),this is equivalent to(2.1)–(2.3)with K=dK0.

Now we prove the sufficient part.

Suppose that the fundamental matrix of(1.2)satis fies the conditions(2.1)–(2.3)for some K＞0.

For a Ψ-sumabble and Ψ-bounded sequence f:Z→ Rd,we consider the sequence u:Z→Rdde fi ne by

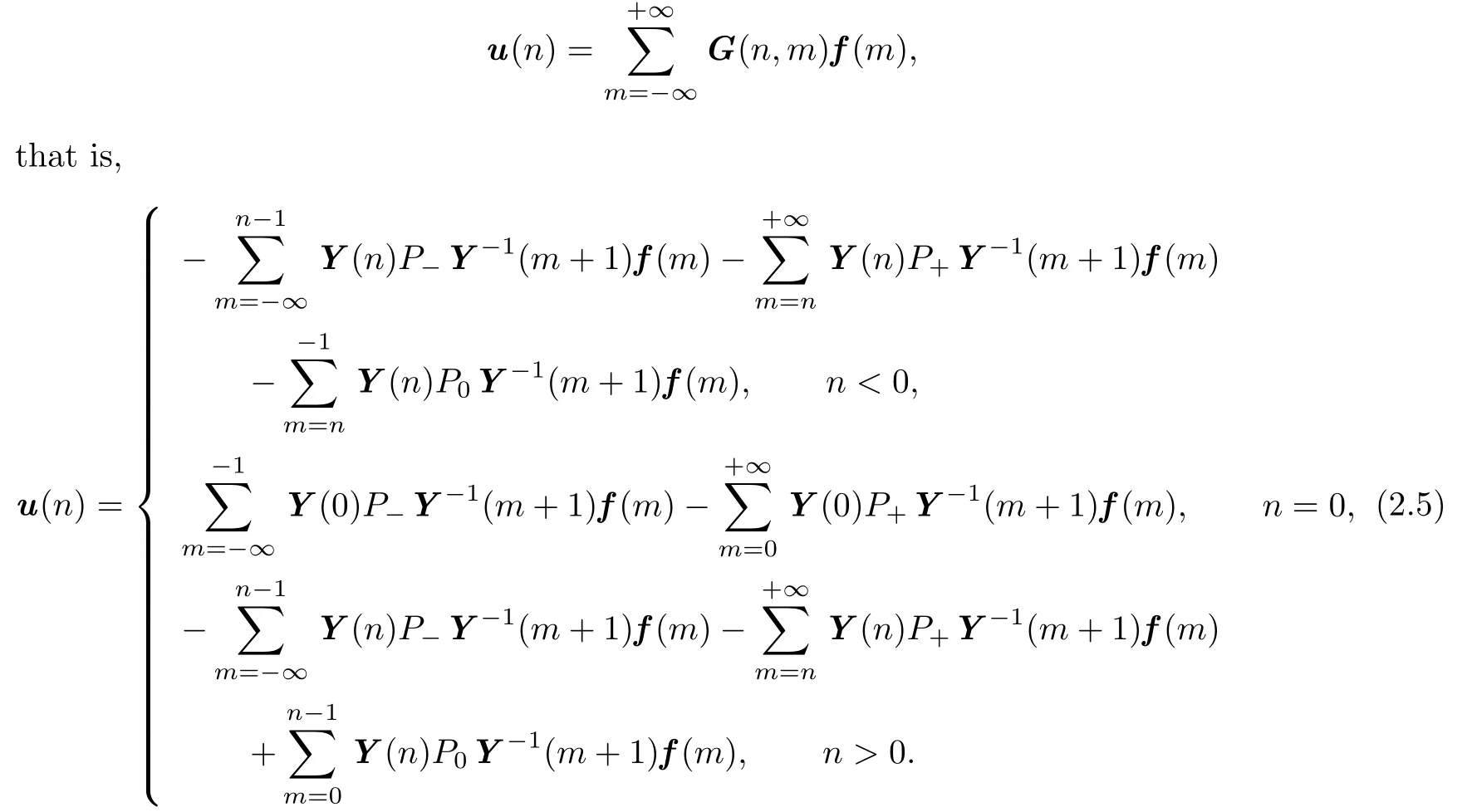
Step 4.The sequence u is well-de fi ned on Z.

For l≥n,we have

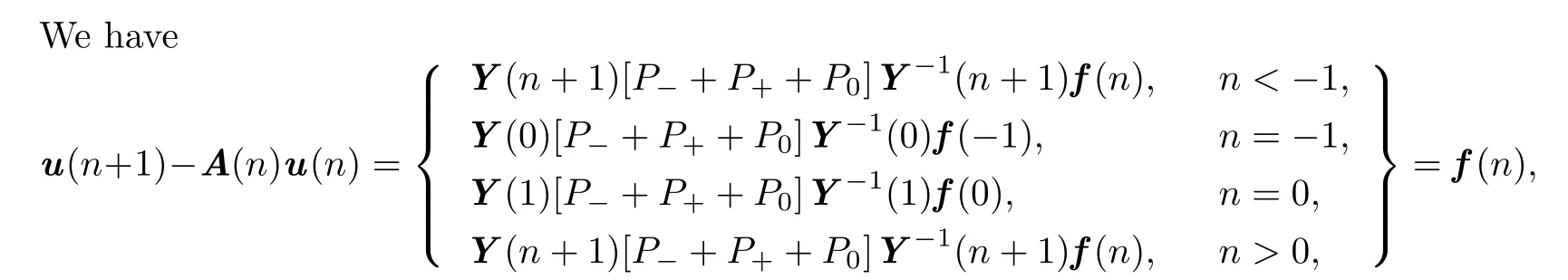
which shows that u is a solution on Z of(1.1).

Step 6.The solution u is Ψ-bounded on Z.

For n＞0,we have

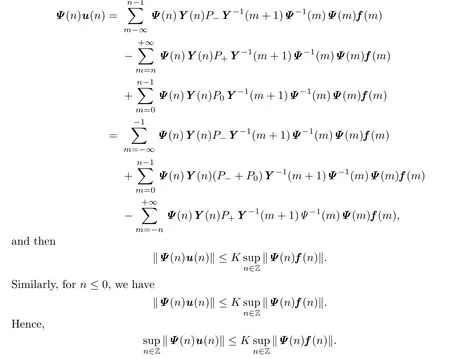
Which shows that u is a Ψ-bounded solution on Z of(1.1).The proof is now completed.

Remark 2.1The Ψ-summableness of the sequence f on N obviously implies the Ψ-boundedness on N of the same sequence,so the Theorem 2.1 improves the result of[9].

In a particular case,we have

Theorem 2.2Suppose that

(1)The fundamental matrixY(n)of(1.2)satis fies

(a)The conditions(2.1)for someK＞0;

(b)The condition

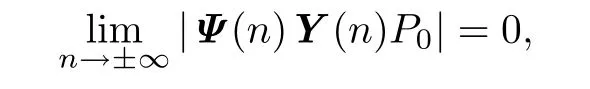
and

(2)TheΨ-summable andΨ-bounded sequencef:Z→Rdis such that

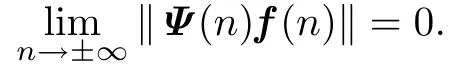
Then everyΨ-bounded solutionxof(1.1)is such that

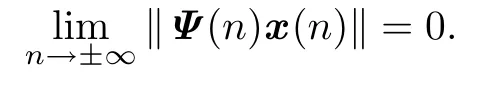
Proof.By Theorem 2.1,for every Ψ-summable and Ψ-bounded sequence f:Z→Rd,the equation(1.1)has at least one Ψ-bounded solution.Let x be a Ψ-bounded solution of (1.1),and u de fi ned by(2.5).This sequence is a Ψ-bounded solution of(1.1).Now,let

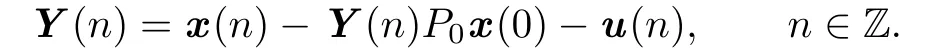
Obviously,Y is a Ψ-bounded solution on Z of(1.2).Thus,Y(0)∈X0.

On the other hand,

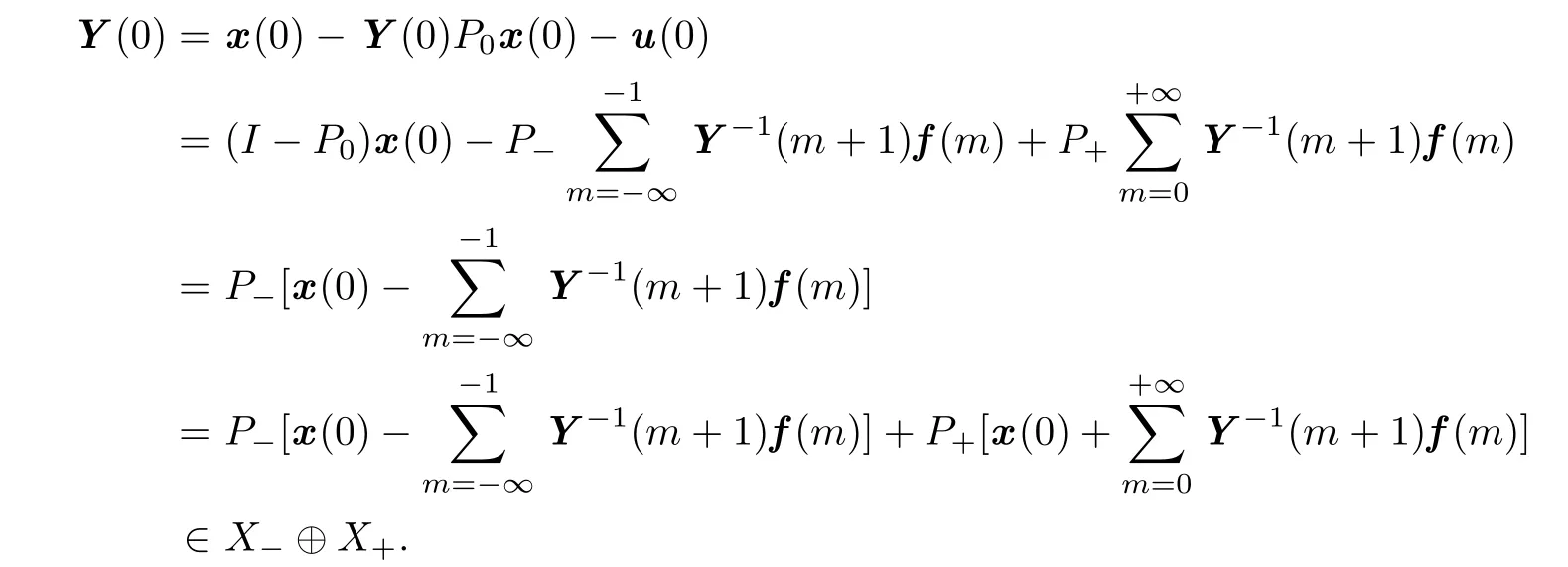
Therefore,Y(0)∈X0∩(X−⊕X+)={0},and then Y=0.It follows that

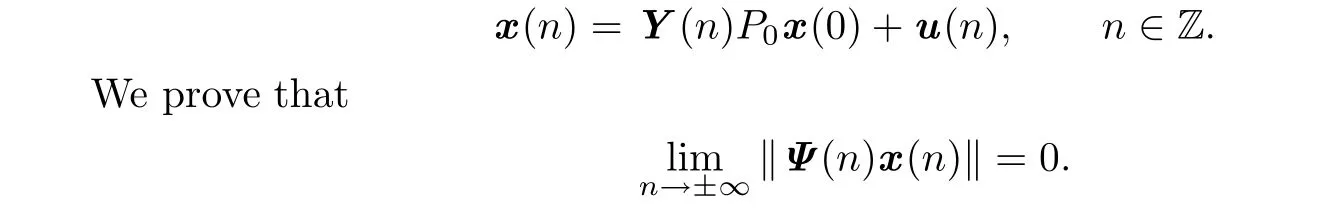
For a given ε＞0,there exists an n1＞0 such that

[1]Agarwal,R.P.,Di ff erence Equations and Inequalities,Second ed.,Marcel Dekker,New York, 2000.

[2]Agarwal,R.P.and Wong,P.J.Y.,Advanced Topics in Di ff erence Equations,Kluwer,Dordrecht,1997.

[4]Palmer,K.J.,Exponential dichotomies,the shadowing-lemma and transversal homoclinic points,Dynam.Reported,1(1998),265–306.

[5]Yoshizawa,T.,Stability Theory and the Existence of Periodic Solutions and Almost Periodic Solutions,Appl.Math.Sci.,Vol.14,Springer-Verlag,New York-Heidelberg,1975.

[6]Coppel,W.A.,Stability and Asymptotic Behavior of differential Equations,Heath,Boston, 1965.

[7]Diamandescu,A.,Note on theΨ-boundedness of the solutions of a system of differential equations,Acta Math.Univ.Comenianae,73(2004),223–233.

[8]Diamandescu,A.,Existence ofΨ-bounded solutions for a system of differential equations, Electron,J.differential Equations,63(2004),1–6.

[9]Diamandescu,A.,A Note on theΨ-boundedness for differential systems,Bull.Math.Soc.Sci. Math.Roumanie,Tome 48(96),1(2005),33–43.

[10]Han,Y.and Hong,J.,Existence ofΨ-bounded solutions for linear di ff erence equations,Appl. Math.Lett.,20(2007),301–305.

[11]Diamandescu,A.,Existence ofΨ-bounded solutions for linear di ff erence equations on Z,Electron.J.Qualitative Theory differential Equations,26(2008),1–13.

Communicated by Li Yong

39A06,39A22

A

1674-5647(2011)04-0331-12

date:Feb.6,2010.

The NSF(Y2008A30,ZR2010AL011)of Shandong Province.