Some Properties of the Beurling-Ahlfors Extension∗

SUN ZONG-LIANGAND LI SHU-LONG

(1.Department of Mathematics,Shenzhen University,Shenzhen,Guangdong,518060)

(2.School of Biomedical Engineering,Southern Medical University,Guangzhou,510515)

Some Properties of the Beurling-Ahlfors Extension∗

SUN ZONG-LIANG1AND LI SHU-LONG2

(1.Department of Mathematics,Shenzhen University,Shenzhen,Guangdong,518060)

(2.School of Biomedical Engineering,Southern Medical University,Guangzhou,510515)

In this paper,we study the Beurling-Ahlfors extensions and prove two results.The first variation of the Beurling-Ahlfors extension is not always harmonic; the Beurling-Ahlfors extension of a quasisymmetric mapping is not always harmonic.

Beurling-Ahlfors extension, first variation,harmonic map

1 Introduction

McMullen[1]proved that the first variation of the Douady-Earle extension is harmonic. Liu and Yao[2]proved that the Douady-Earle extension is not always harmonic.To find nice extensions of quasiconformal(quasisymmetric)homeomorphisms of Snto Hnis an interesting and important problem.Quasiconformal extensions were first constructed by Beurling and Ahlfors[3]in dimension 2 and higher dimensional extensions were given by Tukia and Vlsl[4].Tukia[5]constructed a version that was compatible with the action of the group of Mbius transformations.Douady and Earle[6]constructed a conformally natural version in all dimensions,and for any homeomorphism between the circles,its Douady-Earle extension always exists.Hardt and Wolf[7]showed that the set of quasiconformal (quasisymmetric,if n=2)mappings f:Sn−1→Sn−1which admit quasiconformal harmonic extensions F:Hn→Hnis open in the set of quasiconformal(quasisymmetric,respectively) self-mappings of Sn−1.In[7],the authors also considered the question of finding a harmonic extension which is compatible with Mbius transformations that Royden ever asked.As to this question,Scheon[8]gave a conjecture as follows.For any homeomorphism between the unit circles which admits a quasiconformal extension,there is a harmonic extension on the Poincardisk(the unit disc with the Poincarmetric).Li and Tam[9,10]first constructed these harmonic extensions under some assumptions of smoothness of the boundary mappingsf:Sn−1→ Sn−1and a lower bound on its energy density(see[11]).Non-uniqueness properties of these extensions were also identi fi ed(see[10]and[12]).

It is well known that if the Douady-Earle extension is harmonic,then it coincides with the harmonic extension.Thus it is natural to ask whether the Douady-Earle extension is harmonic.Because if it was,then it would be easier to construct quasiconformal harmonic extensions of quasisymmetric boundary mappings.And,Scheon’s conjecture would be true. However,Liu and Yao[3]proved that the Douady-Earle extension is not always harmonic. Besides,McMullen[1]showed that the first variation of Douady-Earle extension is harmonic (Liu and Yao[2]gave a new proof).

In this paper,we consider the following two questions about the Beurling-Ahlfors extension:Is it true that the first variation of the Beurling-Ahlfors extension is always harmonic? Is it true that the Beurling-Ahlfors extension of a quasisymmetric mapping is always harmonic?Our main results are as follows.

Theorem 1.1The first variation of the Beurling-Ahlfors extension is not always harmonic.

Theorem 1.2The Beurling-Ahlfors extension of a quasisymmetric mapping is not always harmonic.

2 Preliminaries

2.1 Harmonic Map and First Variation

Let D={z∈C:|z|＜ 1}be the unit disk in the complex plane C and S1= ∂D, ¯D=DSS1.Denote by ℜz and ℑz the real part and imaginary part of a complex number z,respectively.Let M be a C∞surface.Consider two metrics σ|dz|2and ρ|dω|2on M, where z and ω are holomorphic coordinates of M.For an arbitrary Lipschitz mapping ω:(M,σ|dz|2)→(M,ρ|dω|2),we de fi ne the energy density of ω to be

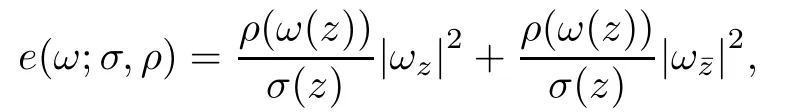
and the total energy to be

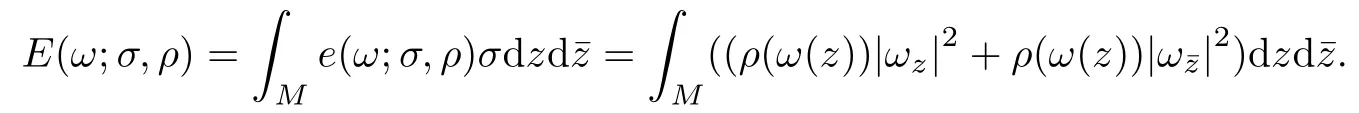
It is easy to see that the total energy depends only on the metric ρ|dω|2on(M,ρ|dω|2), and in fact,depends only on the conformal structure on(M,σ|dz|2).We take the above total energy E(ω;σ,ρ)as a functional of ω,and call its critical map z 7→ω(z)a harmonic map.It is well known that the map z 7→ω(z)is harmonic if and only if it satis fies the so called Euler-Lagrange equation

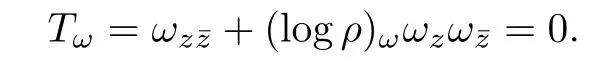
Let V(S1),V(D)and V()be spaces generated by continuous vector fields on S1,D and,respectively.For a smooth vector field f in V(S1),there exists a family of one parameter di ff eomorphisms φt:S17→S1,such that near t=0,there holds uniformly

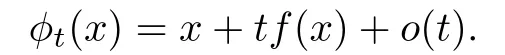
We know that when t is sufficiently small,for the extension Htof φt,there holds

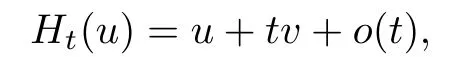
where v∈R2.In fact,this is true for all continuous vector fields.Thus,there is an induced linear mapping L:f 7→v from V(S1)to V(D),we call v=v(x,y)the first variation of the extension Ht.

2.2 Beurling-Ahlfors Extension and Its First Variation

Let T={g(x):x∈R}be a smooth vector field on R.Then we know that,when t is sufficiently small,ht=x+tg(x)is a quasisymmetric function of x.In what follows,we sometimes use h(x)to denote ht(x)=x+tg(x).Let the Beurling-Ahlfors extension of ht(x):R→R be

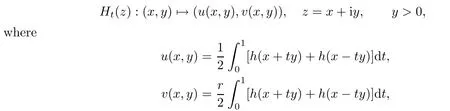
and r＞0 is a parameter.Without loss of generality,we take r=2.To simplify u(x,y)and v(x,y),we observe that

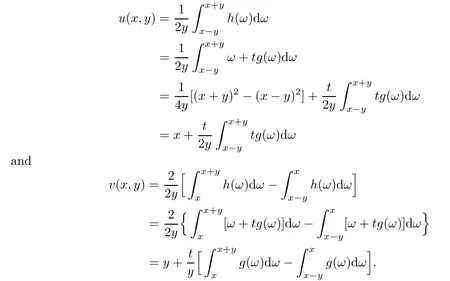
As stated in Section 2.1,for sufficiently small t,we have

Consequently,the first variation of the Beurling-Ahlfors extension Htis

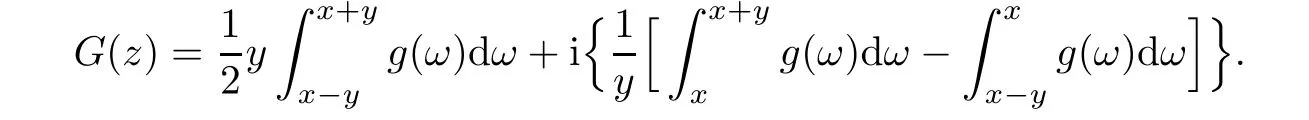
3 Proof of the Main Theorems

Proof of Theorem 1.1We want to show that the above G(z)is not harmonic in the upper half plane.Namely,in the Euler-Lagrange equation,TGis not identically zero in the upper half plane.In fact,we show TG|z=i0.

By simple computations,for G(z)de fi ned in the upper half plane,we have

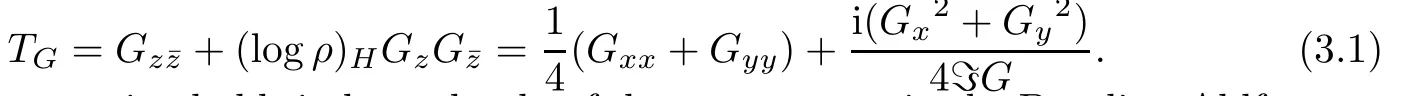
Note that this expression holds independently of the parameter r in the Beurling-Ahlfors extension.Here,we also take r=2 as in Section 2.2.For the above G(z),direct computations give GxGy,Gxxand Gyyas follows:

In the above expressions of Gx,Gy,Gxxand Gyy,taking z=i,namely,x=0,y=1 and g(ω)=ω3,we obtain

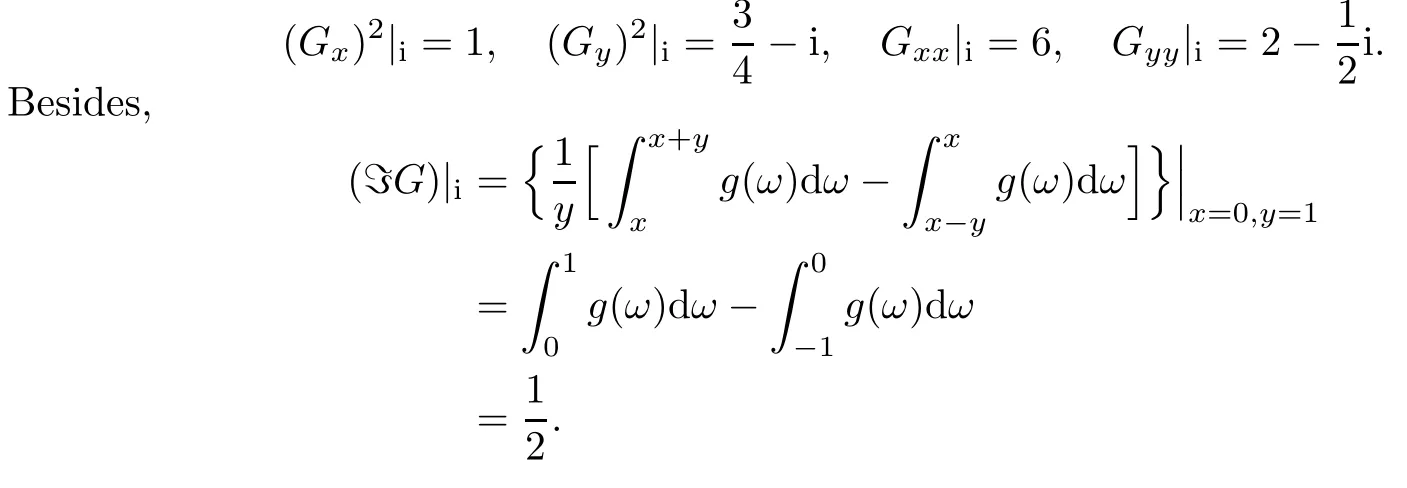
Therefore,by(3.1)we have

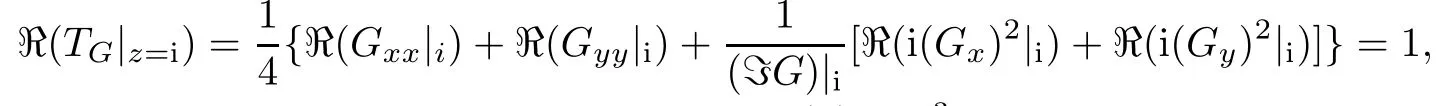
which indicates that for the smooth vector field g(x)=x3on R,we have

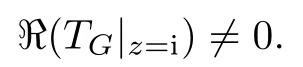
This shows that the first variation of the Beurling-Ahlfors extension of smooth vector field on R is not always harmonic.

Proof of Theorem 1.2It is well known that for each constant k＞1,the mapping

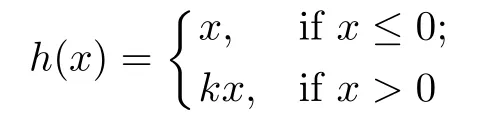
is quasisymmetric.Denote by

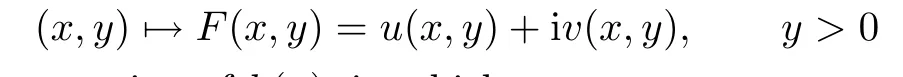
the Beurling-Ahlfors extension of h(x),in which

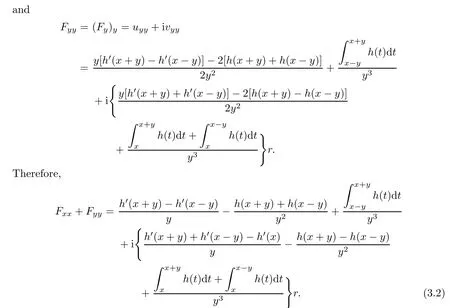
We make the following discussions.

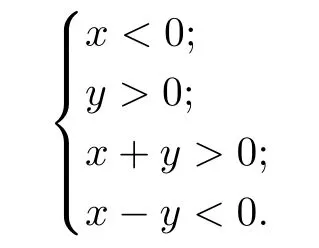
We show that the Beurling-Ahlfors extension

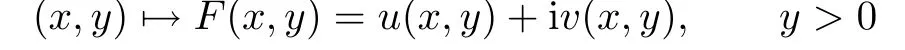
of x 7→h(x)is not a harmonic map in this domain,and therefore neither in the upper half plane.

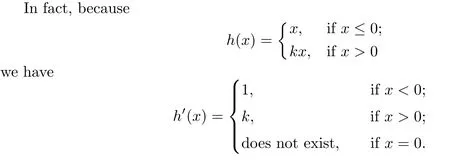
For z=x+iy in the aforementioned domain,we have

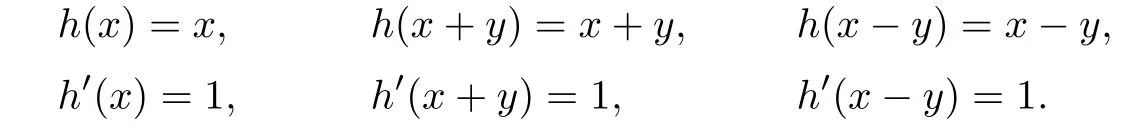
Put these terms into(3.2),we obtain

Consequently,

This shows that F(x,y)is a harmonic function.

Besides,we have

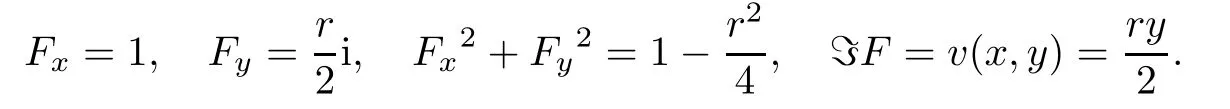
Now,put these terms and(3.3)into(3.1),we get

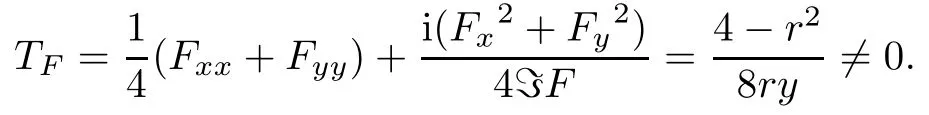
which asserts our conclusion that

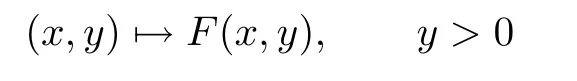
is not a harmonic map in the upper half plane.

(b)When r=2,we study the case that z=x+iy lies in the following domain:

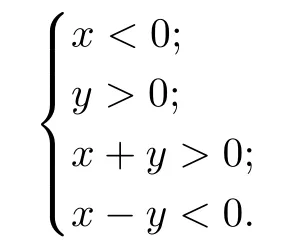
By taking r=2,similarly to the case(a),one easily checks that

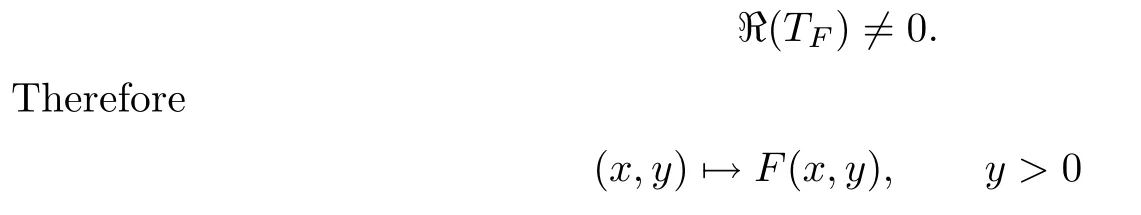
is not a harmonic map in this domain,neither is in the upper half plane. To sum up,the Beurling-Ahlfors extension

of x 7→h(x)is not a harmonic map in the upper half plane.This completes the proof of the theorem.

AcknowledgementThe author would like to express his sincere appreciation to Professor Liu Li-xin for bringing him to this research.

[1]McMullen,C.T.,Renormalization and 3-manifolds Which Fiber over the Circle,Ann.of Math. Studies,Vol.142,Princeton Univ.Press,Princeton,New Jersey,1996.

[2]Liu,L.and Yao,H.,The Douady-Earle extension is not always harmonic,Math.Ann.,preprint.

[3]Beurling,S.L.and Ahlfors,L.V.,The boundary correspondence under quasiconformal mapping,Acta Math.,96(1956),125–142.

[5]Tukia,P.,Quasiconformal extension of quasisymmetric mappings compatible with a Mbius group,Acta Math.,154(1985),153–193.

[6]Douady,A.and Earle,C.J.,Conformally natural extension of homeomorphism of the circle,Acta Math.,157(1986),23–48.

[7]Hardt,R.and Wolf,M.,Harmonic extensions of quasiconformal maps to hyperbolic space,Indiana Univ.Math.J.,46(1997),155–163.

[8]Schoen,R.M.,The role of harmonic mappings in rigidity and deformation problems,in:Komatsu,G.and Sakane,Y.eds.,Proc.of the Osaka International Conf.on Complex Geometry, 1990,Lecture Notes in Pure and Appl.Math.,Vol.143,Dekker,New York,1993,pp.179–200.

[9]Li,P.and Tam,L.F.,Uniqueness and regularity of proper harmonic maps,Ann.of Math., 137(1993),167–201.

[10]Li,P.and Tam,L.F.,Uniqueness and regularity of proper harmonic maps II,Indiana Univ. Math.J.,42(1993),591–635.

[11]Akutagawa,K.,Harmonic di ff eomorphisms of the hyperbolic plane,Trans.Amer.Math.Soc., 342(1994),325–342.

[12]Li,P.and Tam,L.F.,The heat equation and harmonic maps of complete manifolds,Invent. Math.,105(1991),583–591.

54C20,30C62,58E20

A

1674-5647(2011)04-0289-8

date:Jan.18,2006.

The NSF(11101290)for Young Scientists of China,the NSF(11071179,10871211)of China and Scienti fi c Research Starting Foundation(00035242)of Shenzhen University.