Some Remarks on Distributional Chaos for Linear Operators∗

TIAN GENG AND HOU BING-ZHE

(Institution of Mathematics,Jilin University,Changchun,130012)

Some Remarks on Distributional Chaos for Linear Operators∗

TIAN GENG AND HOU BING-ZHE

(Institution of Mathematics,Jilin University,Changchun,130012)

In this paper,we consider some properties for bounded linear operators concerning distributional chaos.Norm-unimodality of bounded linear operators implies distributional chaos.Some properties such as similarity and spectra description for norm-unimodal operators are considered.The existence of distributional chaos in nest algebra is also proved.In addition,we obtain a sufficient and necessary condition of distributional chaos for a class of operators,which contains unilateral backward weighted shift operators.

distributional chaos,norm-unimodality,similarity,spectrum,nest algebra

1 Introduction

A discrete dynamical system is simply a continuous function f:X → X,where X is a complete separable metric space.As we know,the main task to investigate the system (X,f)is to clear how the points of X move,i.e.,to clear the“orbits”.For x∈X,the orbit of x under f is

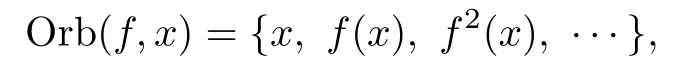
where fn=f◦f◦···◦f is the n-th iterate of f obtained by composing f with n times.

We are interested in the dynamical systems induced by continuous linear operators on Banach spaces.To see the progress of this aspect,we refer the reader to[1]and[2].In this article,we restrict our attention to distributional chaos for continuous linear operators.In [3],distributional chaos is de fi ned in the following way.

For any pair{x,y}⊂X and any n∈N,de fi ne distributional function:R→[0,1] by

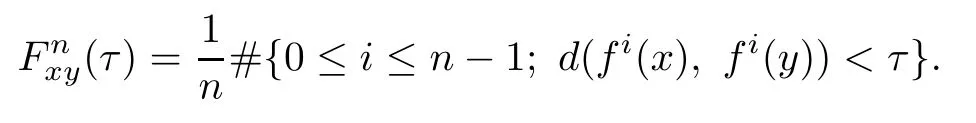
Furthermore,de fi ne

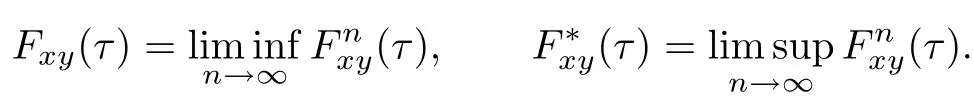
Both Fxyandare nondecreasing functions and may be viewed as cumulative probability distributional functions satisfying

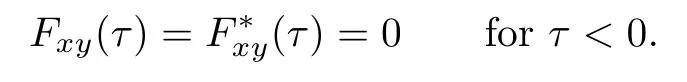
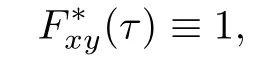
De fi nition 1.1{x,y}⊂Xis said to be a distributionally chaotic pair,if for anyτ＞0,and there existsǫ＞0such thatFxy(ǫ)=0;fis called distributionally chaotic,if there exists an uncountable subsetD⊆Xsuch that each pair of two distinct points is a distributionally chaotic pair,whereDis called a distributionallyǫ-scrambled set.

De fi nition 1.2LetXbe a Banach space andT∈L(X).Tis called norm-unimodal,if there exists a constantγ＞1such that for anym∈N,there existsxm∈Xsatisfying

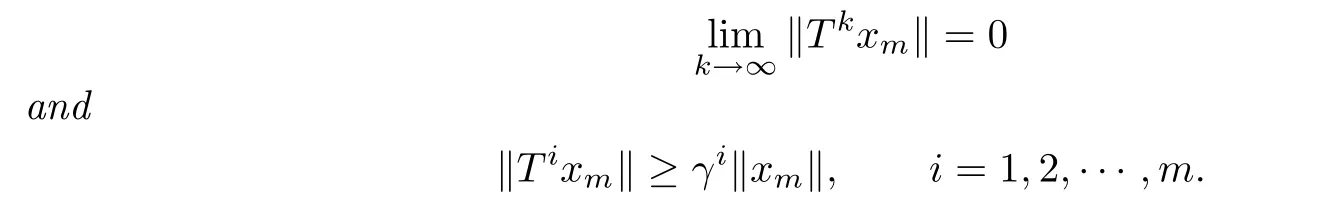
Furthermore,suchγis said to be a norm-unimodal constant for the norm-unimodal operatorT.

Theorem 1.1(Distributionally Chaotic Criterion)LetXbe a Banach space andT ∈L(X).IfTis norm-unimodal,thenTis distributionally chaotic.

However,the converse implication is not true in general.In[6],one can see that normunimodal operators are dense in the set of distributionally chaotic operators in the sense of norm topology.Moreover,the interior of the set of distributionally chaotic operators is contained in the set of norm-unimodal operators.These together show that,in most cases, norm-unimodality can be used as a criterion when we investigate whether an operator is distributionally chaotic.

In this article,we continue to discuss some properties such as similarity and spectra description for norm-unimodal operators.Moreover,the existence of distributional chaos in nest algebra is proved.We also obtain a sufficient and necessary condition of distributional chaos for a class of operators,which contain unilateral backward weighed shift operators.

2 Properties of Norm-unimodal Operators

Proposition 2.1LetXbe a Banach space.LetT,C∈L(X)andCbe an invertible operator.IfTis norm-unimodal,thenC−1TCis also norm-unimodal.

Proof.Firstly,we claim that the following statements are equivalent:

(a)T is norm-unimodal;

(b)There are constants r＞1 and N∈Nsuch that for any m≥N,there exist xm∈X satisfying

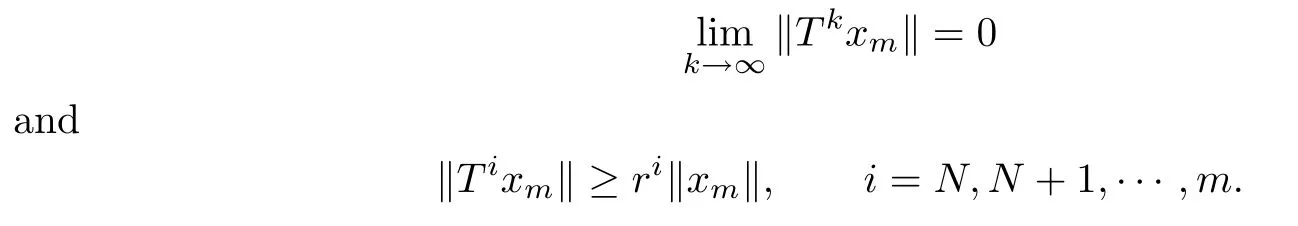
For convenience,denote the property(b)as P(N).

(a)⇒(b)is obvious.

(b)⇒(a):If P(N)holds,then for any m≥N−1,there exist xm∈Nsatisfying

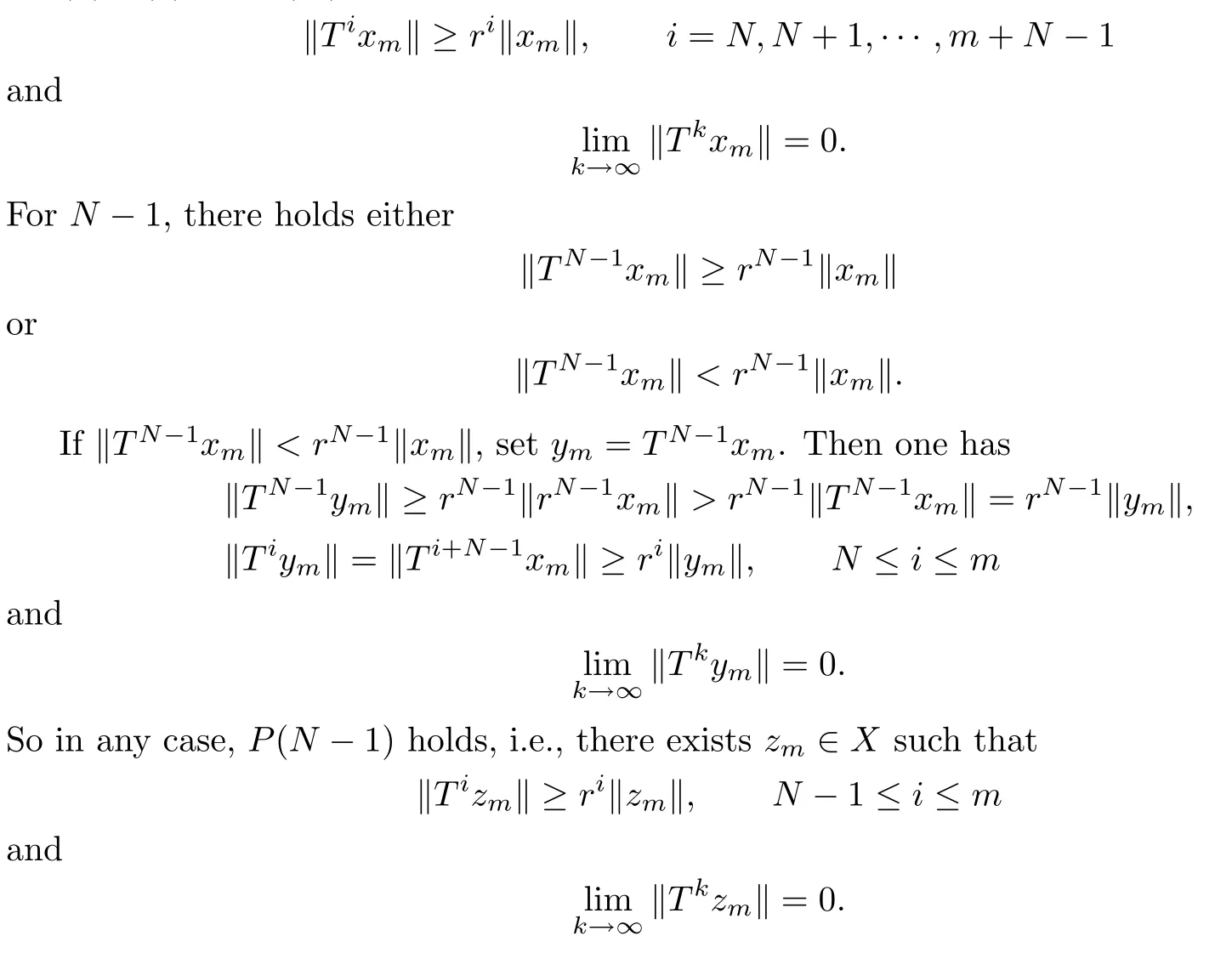
Continuing in this matter shows that(a)is true.

Now it is sufficient to show that C−1TC satis fies(b).

Suppose that T is norm-unimodal.Then there is a constant r＞1 such that for any m∈N,there exists xm∈X satisfying

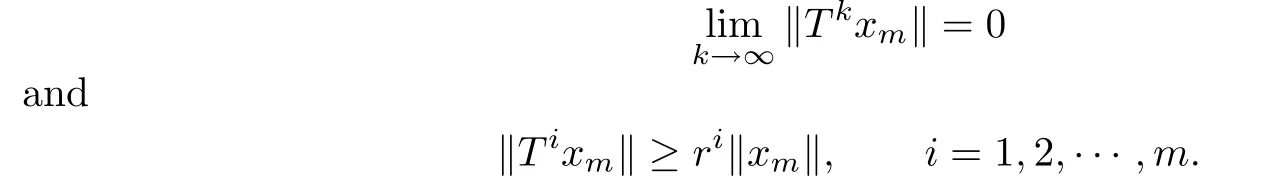
Choose r1such that 1＜r1＜r.Then there exists N1such that for any k≥N1,

Given any m≥N1,for any i with N1≤i≤m one has

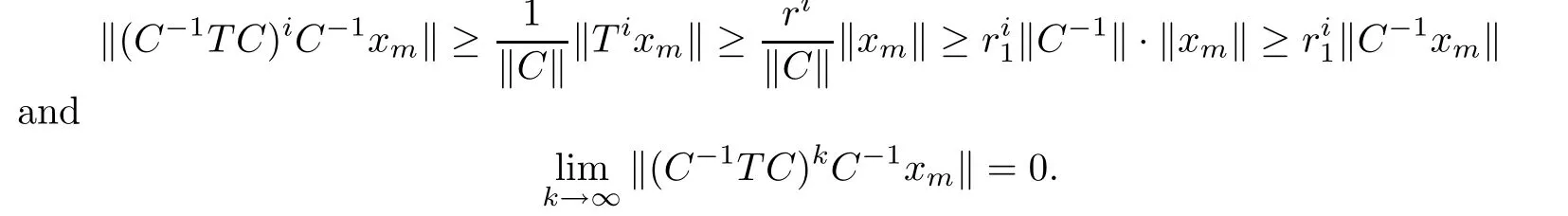
Therefore,norm-unimodality is similar invariant.

The next result gives a description for the spectra of norm-unimodal operators.Denote by D the unit open disk on the complex plane.Moreover,D−denotes its closure and∂D denotes its boundary.

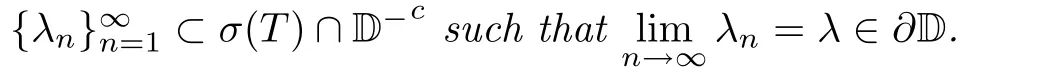
Proof.Suppose that the conclusion were false.Then according to Riesz’s decomposition theorem,we would obtain

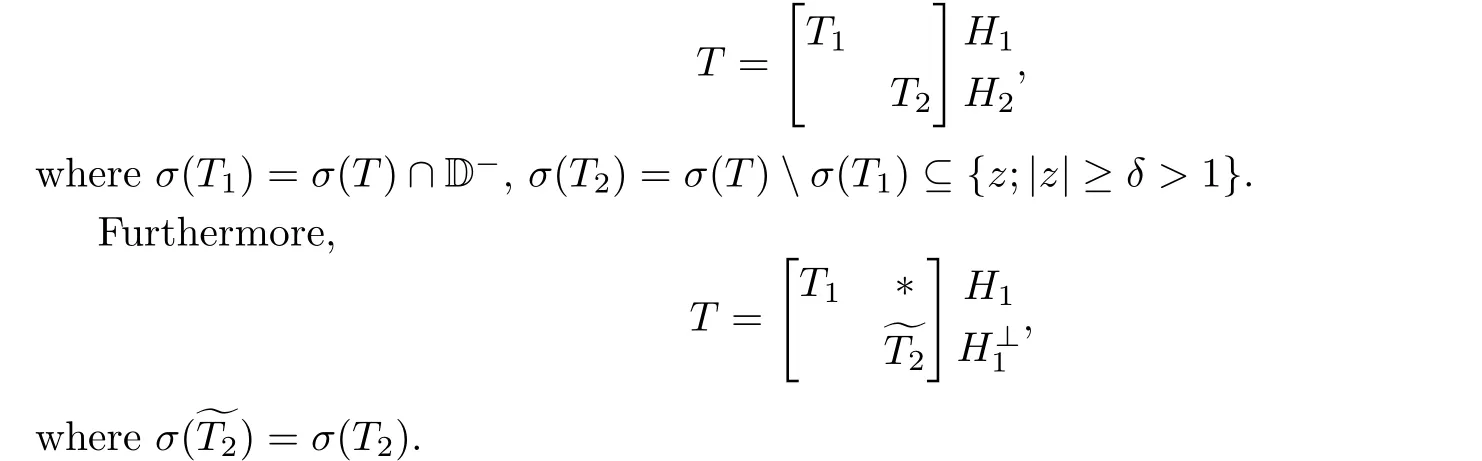
Since T is norm-unimodal,there is a constant r＞1 such that for any m ∈N,there exist xm∈H satisfying

It is a contradiction.

Speaking intuitively,in the spectra of each norm-unimodal operator there should be a sequence of points outside the unit circle which converges to a point on the unit circle.And there exist norm-unimodal operators whose spectra disjoint with the unit open disk.

Example 2.1Let T be a bilateral weighted shift operator with weights{ωn}n∈Zas

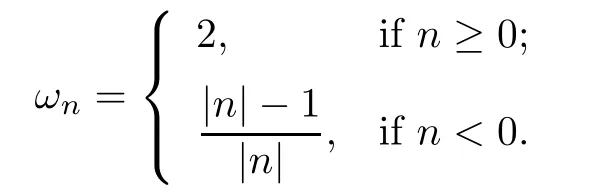
Obviously,T is norm-unimodal,but σ(T)∩D=∅.

3 The Existence of Distributional Chaos in Nest Algebra

In[7],the existence of distributional chaos in nest algebra was discussed but only with respect to a class of nests.In this section,we consider distributional chaos in nest algebra via the technique of norm-unimodality,and get the existence of distributional chaos in any given nest algebra.

De fi nition 3.1A nestNis a chain of closed subspaces of a Hilbert spaceHcontaining{0}andHwhich is closed under intersection and closed span.The nest algebraT(N)of a given nestNis the set of all operatorsTsuch thatTN⊆Nfor every elementNinN.De fi nition 3.2LetNbe a nest.ForNbelonging toN,de fi ne

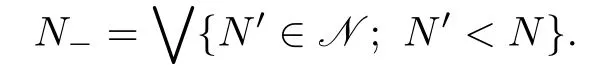
IfN−N,thenN−is called the immediate predecessor toN;otherwise,Nhas no immediate predecessor.

Lemma 3.1T(N)is a weak operator closed subalgebra ofB(H).

The proof can be referred to[8].

Proposition 3.1LetNbe a nest.Then there exists an operatorTinT(N)such thatTis distributionally chaotic.

Proof.If H has an immediate predecessor H1,then H1is considered.Continuing in this manner,we obtain either a chain H＞H1＞H2＞···,or a HMwhich has no immediate predecessor.

For the first case,let Fi=Hi−1⊖Hiand H0=H.Choose fi∈Fisuch that kfik=1. De fi ne

where a1=1 and an−an−1=n.Since each fan+i+1⊗2fan+ibelongs to T(N),A belongs to T(N)by Lemma 3.1.

For the second case,since HMhas no immediate predecessor,there exists a chain N1＜N2＜···＜Ni＜···＜HMin N such that

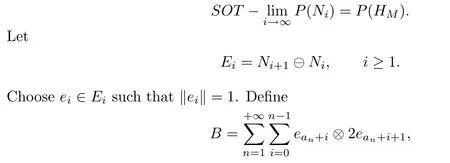
where a1=1 and an−an−1=n.Since each ean+i⊗2ean+i+1belongs to T(N),B belongs to T(N)by Lemma 3.1.

One can easily see that both A and B,under some suitable orthonormalbasis respectively, have the form of matrix as follows:

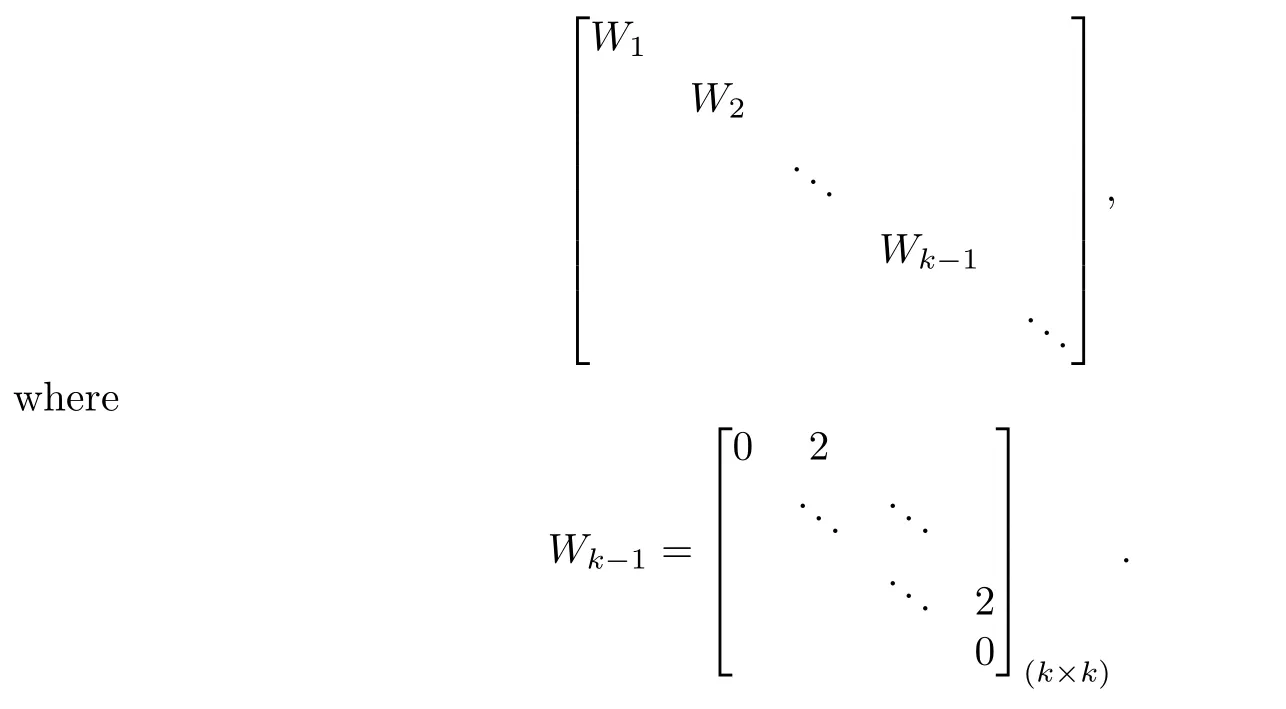
So we obtain that they are all norm-unimodal,and hence distributionally chaotic.

4 A Sufficient and Necessary Condition

Obviously,unilateral backward weighed shift operators satisfy the hypothesis in the previous theorem.

[1]Grosse-Erdmann,K.G.,Recent developments in hypercyclicity,Rev.Real Acad.Cienc.Serie A.Mat.,97(2003),273–286.

[2]Shapiro,J.H.,Notes on Dynamics of linear operators,unpublished Lecture Notes,Available at http://www.math.msu.edu/˜shapiro.

[5]Hou,B.Z.,Cui,P.and Cao,Y.,Chaos for Cowen-Douglas operators,Proc.Amer.Math.Soc., 138(2010),929–936.

[6]Hou,B.Z.,Tian,G.and Zhu,S.,Approximation of chaotic operators,J.Operator Theory, forthcoming.

[7]Li,Y.,Tian,G.,Wu,F.and Hou,B.Z.,The existence of distributional chaos in nest algebras (in Chinese),J.Jilin Univ.(Science Edition),47(2009),948–950.

[8]Davidson,K.R.,Nest Algebras,Longman Scienti fi c&Technical,Essex,1988.

Communicated by Ji You-qing

54H20,37B99,47A10,47A99

A

1674-5647(2011)04-0307-08

date:Oct.22,2009.

The Youth Foundation of Department of Mathematics,Jilin University.