专利实物期权定价的蒙特卡罗模拟方法及其改进技术

马俊海,张秀峰

(1.浙江大学城市学院商学院,浙江 杭州 310011;2.长城证券杭州营业部,浙江 杭州 310012)

一、引 言

专利作为现代企业最重要的无形资产之一,具有很高的价值。专利对于企业募集发展资金,扩大收益回流,形成竞争优势,强化市场地位发挥着巨大的作用;也对企业间转让、兼并、收购等重大商业行为有着重要的影响。因此,对专利进行科学合理定价也成为现代企业管理决策中的重要内容,引起国内外诸多学者的广泛关注。最早的专利定价方法是基于历史成本的DCF方法,而在DCF方法受到广泛质疑的背景下,许多专家提出了不同的分析技术,实物期权分析方法 (ROA)就是在这种情况下应运而生。Trigeorgis(1996)和Kester(1993)在研究中发现,专利作为实物期权与金融期权有着许多不同之处。Scherer(1997)的研究认为,专利回报的概率分布在接近到期日的时段呈现出高度的非对称特征,这意味着对专利回报的预期必须谨慎选择合适的概率分布。Takalo和Kanniainen(1997)对一系列研究项目和专利成果投资的研究得到结论:延迟投资期权的价值同样来自专利实施后引致收益的不确定性,这种期权的价值体现于现实中的推迟市场化现象。近年来也有些学者尝试新的考察角度来解决专利定价问题。Eduardo S.Schwartz(2002)以生物医药专利为例,对专利引致的独占收益与研发激励的关系进行了研究,说明对专利的定价必然受到研发替代的影响,并对两者的数量关系进行了初步的数学表达。Schwartz(2004)又对研发项目和专利成果投资的价值问题进行了比较研究,并使用他在2001年提出的美式期权LSM定价方法进行了初步尝试。Philipp N.Baecker(2007)同样以生物医药技术专利举例,说明了在非完美专利保护环境下,与专利相关的诉讼成本对自主研发构成激励从而降低了专利的交易价值,其创新在于首次将诉讼概率作为模型内生变量而非外生参数,比较好地表达和解决了专利估值中甚为重要的法律风险问题。我国国内的期权定价理论起步较晚,在专利资产定价领域引进实物期权思想也还是近年的事情,有关专利定价的研究大部分都是建立在Black-Scholes模型的基础上的。范银华和粟娟 (2004)对Black-Scholes模型在专利中的应用进行了进一步的探讨,他们将专利看作基于其风险投资公司资产的经营性看涨期权来处理,但仍然没有考虑专利作为期权的美式特征,而且其参数均为给定外生变量,模型十分粗糙。马忠明、刘康泽 (2006)在充分考虑专利技术的生命周期特征基础上,运用实物期权方法中的动态规划方法倒推计算出任意时点的专利价值和专利实施临界值,并给出了具体的计算方法,开辟了国内采取数值方法解决专利定价的先河,但其模型过于简单,使用固定折现率的方式说明作者没有对专利的特殊性质进行深入研究,模拟实证的设定也不令人信服。周英男等 (2009)提出了专利初始静态价值的概念,将专利具体划分为可交易、不可交易、完全不可交易三种类型,利用随机微分方程推导出专利初始静态价值评估的一般形式——不可交易专利初始静态价格的实物期权评估模型。

综合考察目前专利定价领域的研究成果认为,虽然目前在该领域实物期权理论的主流地位已经得到认可,但在理论和实证层面均没有形成公共认可的具体方法,专利性质的特殊性、专利制度的多样性都给现有期权方法的应用带来了困难。本文基于专利的实物期权特征,运用蒙特卡罗模拟方法对专利的实物期权定价问题进行研究与探讨。

二、专利实物期权定价的基本理论及方法框架

(一)专利技术成果定价原理

实物期权思想实际就是用金融期权定价方法解决实物资产定价问题,金融期权定价模型有很多,大致可分为连续时间模型和离散时间模型两大类,本文要探讨的专利的实物期权价值具有一定的特殊性,使我们在模型基本类别的选择上遇到了困难。这个困难来自专利制度规定本身,即现代专利制度普遍采取的年费制使专利在有效期内的缴费点呈离散分布 (一年一缴),但专利成果带来的现金回报在时间上是连续的。而专利的实物期权显然具有路径依赖性质,必然要求在决策点上能够同时衡量预期收益和成本。加入对专利年费的考量能够使我们的定价模型完好地吻合专利持有人的决策树图,却会在算法上制造极大的问题,好在一般来说专利年费的金额都不高,在我国专利年费水平在几百到几千元之间,对于动辄百万数量级的应用技术专利投资而言是完全可以忽略的。

为了求解,需要将收益现金流做离散化处理,因而我们将专利的最大有效期限平均分割成n段,每段时间间隔为Δt。假设现金回报Ci和实施费用 K都在时间点t0,t1,t2…tn上发生;时点ti的专利实物期权价值表示为VROi;ri,i+1是时点ti到ti+1之间的连续复利利率,将通过适当的利率期限结构模型来进行模拟求解。将专利技术成果付诸实施需要追加投资以及其他的费用,我们假设它们的总和为常数K,即在每个实施专利技术的时点上都相同,这样的假设可以使模型简化。而且由于我们在本节开头提到,实施专利之后还可能出现暂时中止和恢复,而技术工艺的每次反复都需要新的追加成本,所以这个假设并不是脱离实际的。

购买决策的作出必然是在专利申请已经获得批准之后,所以购买决策点为初始时点t0,专利的实物期权定价结果VOP将成为交易价格的基准。在购买专利成果后,专利到期前的每一个决策点ti,决定实施专利的条件是:Ci-K>0,此时立即实施专利成果可以预期在当期实现正收益,此刻专利实物期权价值为:

若Ci-K<0,则企业不会于当期实施专利,而是持有专利等待更好的时机。

对时间轴上的三个特殊时点,我们需要作一下补充说明:对于决策树的起始点t0,专利价值VOP=VRO0;在专利最大有效期限的前一年,也是最后一个决策点tn-1,持有人要么实施专利要么放弃,不存在等待期权。在专利到期时点tn,专利权已经不复存在,但原专利技术的生命周期尚未终结,继续使用该技术仍可以在一段时间内获得收益。根据上面分析,专利到期时点tn之后,应用原专利技术的收益可以作为永续年金折现,专利在到期时点tn依然有实物期权价值:

其中,Ri是行业收益的永续折现率,Rd为现金损失率,NCFn=Cn-K。

(二)专利技术成果的回报函数选择

本文基于Scherer(1997)、Pakes(1986)等人的成果及马忠明等 (2006)的分析过程,将在此基础上做些改动。简便起见,将产品生命周期前三个阶段合为一个,该阶段期末tp回报现金流达到最大,最后衰退阶段作为第二阶段,专利到期之后作为第三阶段,专利技术成果应用的回报函数分成三段:

其中C1(t)表示实际自由现金流 (FCF),α是漂移率,φ是波动参数,dzc(t)是与市场组合相关且服从Wiener过程的一个增量。这个式子表示在该阶段专利回报具有单增性质。

在衰退阶段,我们选用以上方程描述FCF的变化过程。

第三阶段:对于高新技术产业而言,技术壁垒不仅是利润的基本保障,而且几乎是唯一保障,因此专利权到期后,如果该技术成果依然能够带来正效益,竞争者就会蜂拥进入并最终导致原专利技术的回报迅速减少,并导致该产品因无利可图而退出市场。为衡量这一阶段的现金流,我们给出一个项目终值的概念,运用永续年金公式来定义项目终值TV,即

其中,NCFn表示专利权有效期最后时点的净收益现金流 (这当然是将收益离散化后的结果), Ri表示折现率,Rd表示净现金流量的损失率。

三、专利实物期权定价的蒙特卡罗模拟实现及其改进

(一)蒙特卡罗模拟方法的基本分析框架

在前面的讨论中我们反复提到,由于独特性是专利的本质属性,专利定价是在不满足无套利条件的情况下进行的,这给我们带来两个层面上的困难:在宏观层面,这意味着不论市场效率如何,市场内部定价法是无效的;在微观层面,我们不得不使用某种数值方法而非其他看上去简易得多的期权定价模型。作为一类重要数值分析方法,Monte Carlo模拟方法具有两个比较明显的优势:一是比较灵活、易于实现和改进,所以应用领域非常广阔;二是其估计的标准差独立于解决问题的维数,这个特点使Monte Carlo模拟非常利于解决复杂的实物期权定价模型。就本文研究来说,要对专利回报现金流需要进行离散化模拟,至少需要将20年的专利最大有效期限划分为数十段才能取得比较好的拟合效果。因此在维数特征上具有明显优势的Monte Carlo模拟方法是我们的必然选择。我们已经建立了专利实物期权定价的理论模型,通过Monte Carlo模拟方法的应用,可以很容易地实现它。

首先,将专利的最大有效期限均分为n个时间段,时间轴上将有n+1个节点,分别是t0……tn,分段要达到一定的数量以确保离散化效果;其次,根据专利成果回报函数和初始回报C0,应用随机数发生器产生一串离散的回报现金流C1……Cn;再次,使用随机数发生器,根据随机利率模型,产生一串短期利率r1……rn,作为每个时间段上的折现利率;最后,根据我们上面的分析,利用上面两步模拟得到的数据,从后向前依照实施专利的触发条件决定每个时间点上的决策,形成专利实物期权的实施路径,并得到该路径初始点t0的实物期权价值VOP。将上述全部过程重复若干次,结果的算术平均值即作为最终的专利价值。

(二)随机利率模型的选择

在上一节我们建立专利实物期权定价模型的过程中,对连续的专利现金回报进行离散化处理的方法是折现到决策点,由于真实的市场利率是不断变化的,所以对现金流折现法要面对的关键问题就是利率变动模式的估计。由于专利的地域性,在专利定价过程中选择利率模型必须从专利所在国利率体系特征出发,就使利率模型选择分为两个层次:首先要选择最能够代表市场利率;然后通过选择合适理论模型,运用适当参数估计方法得到模型的参数。关于市场利率基准的选择,应该反映市场交易者对市场资金供求状况的真实感受以及资金的真实价格,这种资金价格可以从市场上交易的债券,尤其是无违约风险的国债价格中反映出来,也可以由货币市场利率来近似。关于市场利率期限结构的实证成果和筛选,兼顾代表性和简易性,我们在国内的研究文献中选取单因子模型的研究成果作为我们的模拟实证对象;这类研究中,潘冠中等 (2004)基于对中国银行间拆借利率的实证研究得出的CKLS模型是比较成熟的成果,后来,马晓兰、潘冠中 (2006)综合了Vasicek、CIR、Brennan-Schwartz、CKLS以及Ait-Sahalia模型中对飘移项形式的假设进行了进一步的研究,完善了这个模型。

本文的实证模拟将使用季度时间分隔 (0.25年),所以用于回归的历史数据应该相应为季度数据,为避免直接引用季度收盘价 (或中间价)造成过多的奇异值,同时也为了获得更好的时效性,笔者通过国研网 (www.drcnet.com.cn)数据库获得R007从1998年7月至2007年6月间共108个月度收盘数据,转化为季度均值,作为回归估计的对象——选取银行间拆借市场利率作为短期利率替代品的理由是我国的银行间拆借市场先于债券回购市场一年多开始运行,包括了更长时期的时间数据,拆借利率更能全面反映我国货币市场利率的特点,而选中R007则是由于这个品种是银行间市场交易量最大的品种,且每周都有交易,连续性比较好。通过求解L(Θ)最小化问题,可得到参数估计值如下:

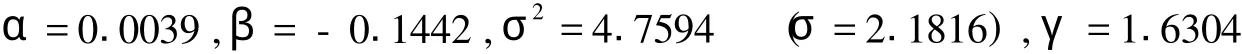
这组参数的估计效果和拟合检验见下表:

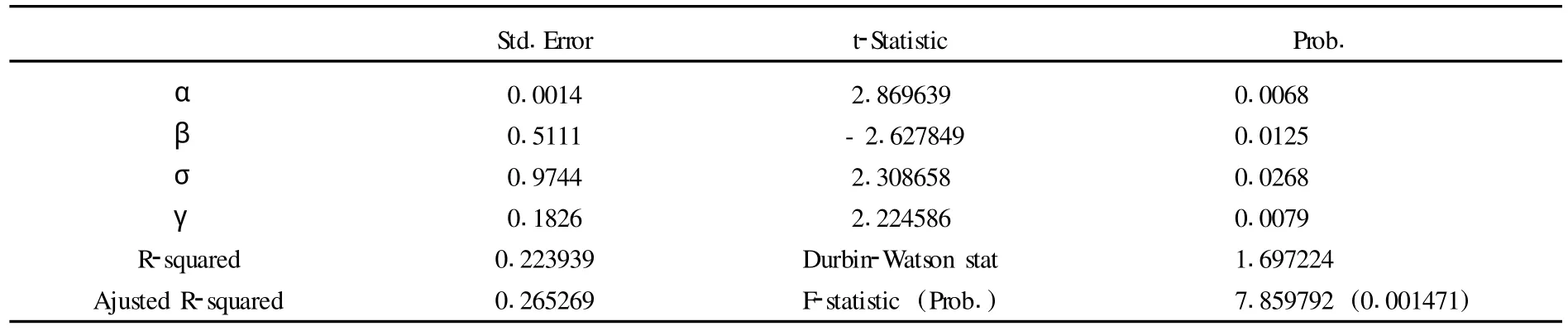
表1 参数回归的检验结果

从SPSS拟合检验的效果来看,各参数的显著性比较有保障,但模型总体的拟合度不是很高,这是可以预见和接受的结果——现实中利率并非完全内生变量,而是深受政策影响,长达9年的采样时间跨度涵盖了上世纪九十年代至今的加息——减息——再加息的政策变动历程,所以不可能获得很高的拟合度;另一方面,Durbin-Watson检验值略小说明利率运动可能具有一定的自相关性,这作为统计检验结果也许是个缺憾,但却与现实更加吻合。

(三)Monte Carlo模拟方法的对偶变量技术及其运用

Monte Carlo模拟方法虽然相对于其他数值方法具有维数独立性和收敛较快的优点,但从客观角度来讲该方法作为非解析算法,其运算效率依然是比较低的,选择适当的方差减少技术显得尤其必要。本文在此决定只对专利回报现金流进行方差减少优化,并且选用理论上最简易的对偶变量技术来实现。对偶变量技术意在通过在每一对模拟路径间引入负相关性来抵消消除一部分方差。简单来说,对偶变量技术就是在每次模拟计算时同时进行两个模拟过程:一个是按照普通蒙特卡罗模拟方法抽取一组随机样本得到结果;另一个是取相应的对偶随机样本得到模拟结果;最后取这两个模拟过程的结果的平均值,即为所求的最终结果。就本文的研究对象而言,使用正态分布作为随机数生成的分布,符合使用对偶变量技术的条件,应用该技术时,首先根据随机抽取生成的样本Zi(i= 1,2,3…n)得到模拟值Ci(i=1,2,3…n),根据Ci产生专利实施策略的路径一条,可以计算得到一个VOP,将此过程重复模拟m次,可以得到Monte Carlo模拟估计值为:

现在我们以Zi(i=1,2,3…n)为基础,构造对偶随机数Zj=-Zi,由正态分布性质可知Zj(j=1,2,3…n)也服从正态分布,将此过程亦模拟m次,由对偶随机数生成的估计值为:

如果随机抽样得到的样本Zi(i=1,2,3…n)模拟得到的估计值较小,则与之对应的对偶随机变量Zj(j=1,2,3…n)模拟得到的估计值可能偏大,二者的平均值就可能接近真实值。

这样我们就利用对偶变量技术实现了减小模拟方差的目的,而计算量的增加是很有限的。在应用了方差减小技术后,优化后的专利实物期权定价流程如下:

首先,将专利的最大有效期限均分为n个时间段,时间轴上将有n+1个节点,分别是t0……tn,分段要达到一定的数量以确保离散化效果;其次,根据专利成果回报函数和初始回报C0,应用随机数发生器产生一串离散的回报现金流C1……Cn;同时生成对偶变量,产生另外一串回报现金流C1＊……Cn＊;第三,对两组由对偶随机数产生的模拟现金流求平均值,得到,作为模拟运算使用的现金流数据;第四,使用随机数发生器,根据随机利率模型,产生一串短期利率r1……rn,作为每个时间段上的折现利率;第五,根据我们上面的分析,利用上面两步模拟得到的数据,进行路径模拟,并得到该路径初始点t0的实物期权价值VOP;最后,将上述全部过程重复若干次 (次数要足够大),可以得到若干定价结果,这些结果的算术平均值即可作为专利价值。

四、专利实物期权定价的实证模拟

我们前面的几章中建立并完善了专利实物期权定价的简易模型,为了能更直观地看到Monte Carlo模拟方法在解决基于实物期权方法的专利估价的应用框架,我们选择了具有代表性的生物制药行业新药专利作为案例进行详细的分析。

(一)案例说明

本文的目的是探讨具有最一般性的专利定价方法,因而我们在满足“理论上正确,原则上可行”的前提下,运用上文建立的简洁型定价模型对最具典型性的专利——生物医药行业新药专利进行模拟实证。本文的模拟实证对象采用来自马黎 (2004)对新药研发项目进行定价所使用的实证范例,并在此基础上作了适当的修改以使符合需要。在该示例中,医药企业提供的通过合理估算和预测得到的新药A在未来时间里的损益情况说明,2009年市场化开始阶段的FCF为34.88(百万),预计在第六年达到最高峰,即专利成果收益的第一阶段持续6年。模拟的时间步长为三个月,即一季度,假设将专利成果规模化带来的季度成本为固定值100(百万)。该案例的相关参数见下表,随机利率模型的参数参照第四部分,初始市场利率赋值为2.5%。

表2 演示案例相关参数值

(二)结果分析

(1)模拟实证案例求解结果。根据本文设计的基本专利实物期权定价模型在matlab环境下编制程序,代入各项参数后得到Monte-Carlo模拟估计结果,具体实现步骤如下:

首先,为了尽量避免和减少循环和重复命令,我们使用矩阵算法来达到一次得解的效果。将模拟运算次数m定为模型中所有随机自变量矩阵的行数,由于我们将专利的最大有效期限均分为80个时间段 (每段0.25年),时间轴上将有81个节点,分别是t1……t81(MATLAB生成数列没有0项),我们将得到m×80随机利率矩阵和m×81现金流矩阵。

然后,根据专利成果回报函数和初始回报C1,应用随机数发生器产生一串离散的回报现金流C1……C81,共产生m行构成m×81矩阵,其发生式为:

第一阶段

同样使用随机数发生器,根据随机利率模型,产生一串短期利率r1……r80,作为每条模拟路径上各时间段的折现利率,共生成m行利率数列,以构成m×80矩阵,其发生式为:

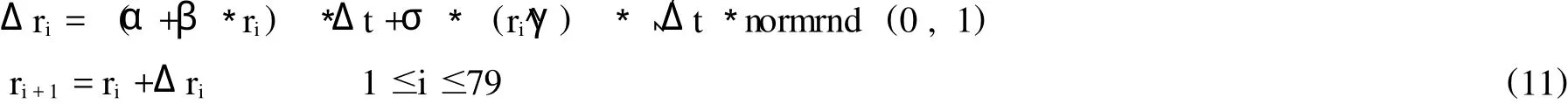
最后,利用上面两步模拟得到的现金流和随机利率数列,计算每个决策点上实施和等待策略的净现值,比较两者以作出最优决策,从而从后向前形成专利实物期权的实施路径,并通过递推运算得到每条路径初始点t1(即定价时点)的实物期权价值VRO1。数学表达如下:

最后一个决策点t81上的专利技术成果价值为:

递推算式为:

如果将所有的VRO列成矩阵形式,则根据Monte Carlo模拟方法原理,最终的专利价值即为该矩阵的第一列元素的算术平均值:

该新药专利的实物期权价值为1118.11(百万),方差6618.24,95%置信区间为 [934.62, 1301.60]。

(2)收敛性分析与方差减小技术的效果。如果我们分别选择模拟次数为2500次和10000次,则可以观察到随模拟次数增长,运算结果呈现出一定的收敛性:

表3 专利价值收敛性分析

进一步增大模拟次数到20000次,可以得到理论上更接近于真值的结果1149.88(百万),95%置信区间为 [1036.70,1263.06],但方差却令人诧异地扩大为8266.13,如果继续增大模拟次数,可以观察到方差的不规则盈缩,但置信区间却保持着稳定的收敛性——由于理论上难以解释这种现象,两者的不协调只好被归因于个人电脑在应对大量运算时的数据溢出可能。好在实际运用中我们拥有其他手段接近精确值:从表3可以看到,在模拟次数增加一倍的情况下,方差和置信区间的缩小都十分有限,如果要显著提高模拟运算效率,应该依靠引入优化方法来实现,于是我们将第四章讨论并选取的优化方法——对偶变量技术嵌入程序。5000次模拟下,优化后的运算结果为1204.87,方差4830.10,一举削减了近1/3的方差,显示出良好的效果——虽然看上去运算结果的置信区间 [1070.96,1338.78]似乎仍然较大,但实际上对于高度不确定的技术密集型产业项目定价来说,该宽度已经可以接受。

五、结论分析

本文紧紧围绕Monte Carlo模拟方法在基于实物期权的专利投资决策中的应用而展开论述,主要做了以下工作:

(1)分析了专利的实物期权特性,并以此为基础,评述了以DCF为代表的传统投资决策方法的缺陷,说明实物期权方法在专利定价领域的比较优势。

(2)由于专利所隐含的期权具有典型的路径依赖特征,不能用解析方法求解,因此需要使用数值方法,考虑几种数值方法优劣,选择Monte Carlo模拟方法用于专利实物期权定价。

(3)通过对专利特征的具体分析,我们发现了由Longstaff&Schwartz(2001)提出的最小二乘蒙特卡罗模拟 (LSM)方法在该领域应用的缺陷,此外对专利制度的研究还使我们获得了包含专利年费考察的完整的专利实物期权定价模型。

(4)为了更好、更直观地说明Monte Carlo模拟方法在专利实物期权定价中的应用,本文选用了具有代表性的生物制药行业的一个新药研发项目进行实证分析。

虽然本文给出了解决专利定价问题的简明方法,为专利投资决策提供了参考,但是由于专利投资本身存在着较大的复杂性,个别专利的独特性使得模型在具体应用中还应根据具体情况进行更细致的分析,模型中还有很多问题值得注意和有待进一步的研究和解决。

(1)成本和现金流的不确定性是专利定价困难的主要来源,但是作为衡量这两者不确定性的波动率参数的估计仍然是个难题。

(2)专利定价问题主要出现在技术型行业且周期较长,长达10年甚至20年的专利有效期限里,突发事件对其影响的可能性是非常大的;本文建立的模型隐含假设专利回报现金流的高度波动性包含了未来一切风险因素,其科学性还有待探讨。

[1]于乃书,刘兆波,张屹山.专利权评估的两种方法探讨 [J].数量经济技术经济研究,1999,(2):3-5.

[2]周英男,李昕杨,王雪冬.专利初始静态价值的实物期权评估模型研究 [J].科学学与科学技术管理,2009,(6):9-12.

[3]杨春鹏,伍海华.实物期权在专利权价值评估中的应用 [J].系统工程理论与实践,2000,(6):101-103.

[4]马忠明,刘康泽.应用期权方法评估专利价值 [J].中南财经政法大学学报,2006,(3):59-63.

[5]范龙振.短期利率模型在上交所债券市场上的实证分析 [J].管理科学学报,2007,(2):80-89.

[6]潘冠中,邵斌.单因子利率模型的极大似然估计——对中国利率的实证分析 [D].上海:上海财经大学,2004.

[7]马黎.实物期权在R&D项目投资决策中的应用——制药甲厂A药品研发项目案例分析 [D].武汉:武汉大学,2004.

[8]Dixit,A.K.,Pindyck,R.S..Investment under Uncertainty[M].Princeton University Press,1994:101-106,108-112,353-356.

[9]Dixit,A.K.,Pindyck,R.S..The Optiongs Approach to Capital Investment[J].Harvard Business Review,1995,(May-June):105-115.

[10]Trigeorgis,L..Alog-transformed binomial numerical analysismethod for valuing complexmulti-option investments[J].Journal of Financial and Quantitative Analysis,1991,26(3),309-326.

[11]Schwartz.E.S.Patents and R&D as Real Options[E/B].University of California:College Working Papers,2002.

[12]Baecker,P.N.An option-based view of imperfect patent protection[E/B].Department of Finance,European Business School:College Working Papers,2007.

[13]Lidebrandt,T..Variance Reduction-Three Approaches to Control Variants[J].Mathematical Statistics,2007:9-13.