时间变量离散动力系统的分布混沌

王立冬，李英男

(1.大连民族学院理学院，辽宁大连116605;

2.辽宁师范大学数学学院，辽宁大连 116029)

时间变量离散动力系统的分布混沌

王立冬1，李英男2

(1.大连民族学院理学院，辽宁大连116605;

2.辽宁师范大学数学学院，辽宁大连 116029)

研究了度量空间中具有时间变量的离散动力系统的分布混沌，介绍了时间变量系统的按序列分布混沌概念，证明了两个一致拓扑等价共轭的时间变量系统有相同的按序列分布混沌的拓扑性质。

时间变量离散系统;按序列分布混沌;拓扑共轭

自从Li和Yorke在1975年首次用严格的数学语言给出了混沌的定义以来［1］，混沌的研究已在现代科学方面产生了深远的影响，Li－Yorke混沌定义的各种延伸也被发展起来。例如，Devaney混沌、Wiggins混沌、Dense混沌、Generic混沌、分布混沌和按序列分布混沌［2］。分布混沌主旨在于利用相同的统计假设来加强“Li－York对”的定义。具有时间不变量的离散系统xn+1=f(xn)(n≥0)的混沌已经被研究，其中f:D⊂X→X是一个映射，(X，d)是一个度量空间，并且获得了许多重要成果。此外，对于高维和无限维映射的研究也取得了一些重要进展。同时，一般时间变量离散系统(TVDS)也被研究［3－4］。一般时间变量离散系统(TVDS)可以写成下列形式:

式中，fn:Dn→Dn+1是一个映射，Dn是度量空间(X，d)的一个子集。不要求fn可逆，只考虑系统(1)的正轨道，Y.Shi和 G.Chen［5］研究了有限维线性时间变量动力系统的混沌，以及关于TVDS的Li－Yorke混沌和Devaney混沌，并且研究了两个拓扑共轭系统之间的动力学行为的联系。表明了仅仅是拓扑共轭通常并不能保证两个拓扑共轭时间变量系统有相同的拓扑性质。

本文研究了关于两个一致拓扑等价共轭时间变量系统的按序列分布混沌的性质，我们考虑两个时间变量系统(1)和

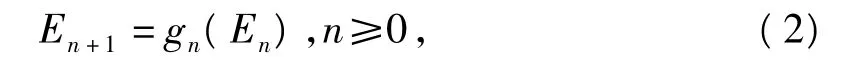
式中，gn:En→En+1是一个映射，En(n≥0)是度量空间(Y，ρ)的一个子集，证明了如下结论:

定理假设系统(1)和(2)是一致拓扑等价共轭，若系统(2)是按序列分布混沌的，则系统(1)也是按序列分布混沌的。

1 基本定义

全文中，(X，d)表示以d为度量的度量空间，fn:Dn→Dn+1是一个映射，Dn是度量空间(X，d)的一个子集。令S是一个至少包含两个不同点的D0的子集，x0，y0∈S，x0≠y0，{pk}是一个正整数序列。对于∀δ＞0，令

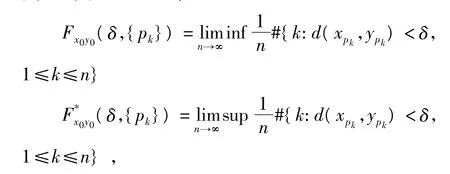
式中，#S表示S中元素的个数。

定义1 S被称为系统(1)的按序列分布混沌集，如果存在一个正整数序列{pk}使得对于∀x0，yo∈S，两个相应的轨道满足

若系统(1)有一个不可数的按序列分布混沌集，则称该系统是按序列分布混沌的。

现在，引入TVDS中拓扑共轭和一致拓扑等价共轭的概念。

2 定理的证明

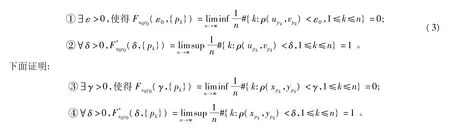
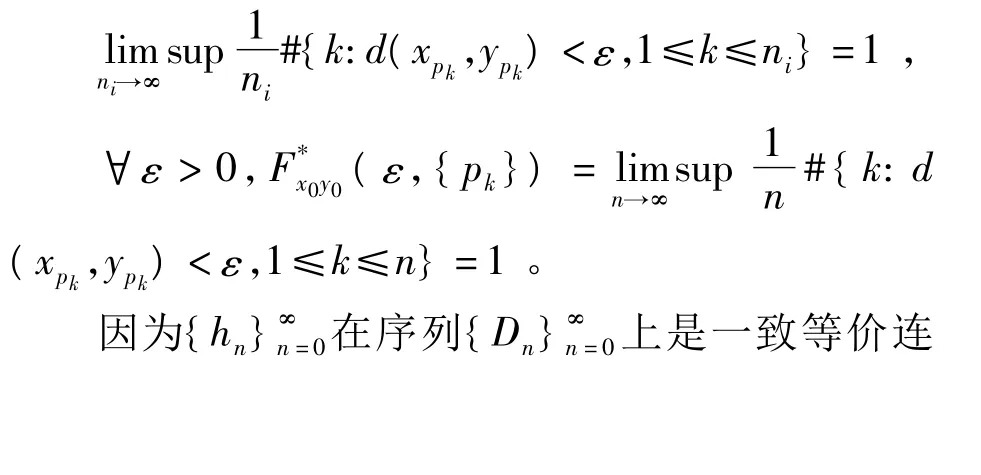
［1］ LI Tianyan，YORKE J A.Period three implies chaos［J］.Amer.Math.Monthly，1975，82:985 －992.

［2］WANG Lidong.Distributional chaos in a sequence［J］.Nonlinear Analysis，2007，67:2131 －2136.

［3］MAROTTO F R.Snap－back repellers imply chaos in［J］.J.Math.Anal.Apl，1978，63:199 －223.

［4］MAROTTO F R.On redefining a snap－back repeller［J］.Chaos Solitons Fractals，2005，25:25 －28.

［5］SHI Yuming，CHEN Guanrong.Chaos of time － varying discrete dynamical systems［J］.Journal of Different E-quations and Applications，2009，15:429 －449.

Distributional Chaos of Time－varying Discrete Dynamical System

WANG Li－dong1，Li Ying－nan2
(1.College of Science，Dalian Nationalities University，Dalian Liaoning 116605，China;
2.School of Mathematics，Liaoning Normal University，Dalian Liaoning 116029，China)

The distributional chaos of time－varying discrete systems in metric spaces has been investigated.The concept of distributional chaos in a sequence for general time－varying systems has been introduced.The conclusion that two uniformly topologically equiconjugate time－varying systems have the same distributively chaos in the sequence has been proved.

time－varying discrete system;distributional chaos in a sequence;topological conjugacy.

O189

A

1009－315X(2011)05－0462－03

2011－05－25;最后

2011－06－14

中央高校基本科研业务费专项资金资助项目(10010101);辽宁教育厅基金项目(2009A141)。

王立冬(1955－)，男，吉林德惠人，博士，学校特聘教授、优秀教学带头人，硕士生导师，主要从事拓扑动力系统研究。

(责任编辑 邹永红)