工业生产中一个带有拒绝费用的工件排序问题研究

冯 琪，杨丽华

（中原工学院，郑州450007）

工业生产中一个带有拒绝费用的工件排序问题研究

冯 琪，杨丽华

（中原工学院，郑州450007）

在工业生产中，生产决策者为了获得最大利润，可能接收一个工件，也可能拒绝一个工件．为了解决哪些工件应该被接收，哪些工件应该被拒绝问题，本文研究了工业生产中一个带有拒绝费用的工件排序问题，对该问题设计了一个动态规划算法．

排序；拒绝；动态规划算法

所谓排序，就是在一定的约束条件下对工件和机器按时间进行分配和安排加工次序，使一个或多个指标达到最优．作为运筹学和管理学的一个重要分支，机器排序理论有着深厚的背景和广阔的应用前景．例如，如果我们把现有的资源（如人力、资金、工具等）当成机器，把所要完成的任务当成工件，那么其他领域的许多问题都可以转化成一个机器排序问题．目前，关于排序理论的研究成果已经应用在许多不同的领域，包括计算机科学及工程、供应链管理、物流运输等领域．因此，从广义上来说，机器排序可以理解为最优地分配有限资源以完成给定的任务．

在大多数经典的排序文献中，都是基于以下假设：所有的工件都必须在机器上加工，不允许拒绝任何工件．然而，在现实中这些假设并非总是成立的．由于资源的有限性，在实际中生产决策者经常会拒绝一些耗费资源且利润较低的工件．如果拒绝一个工件，有时候基于信用或其他因素，不得不支付一个确定的拒绝费用．

可拒绝工件的排序问题是一种新的排序模型．关于这方面的研究还比较少．Bartal Y等人首先考虑了带有拒绝费用的排序问题，他们的目标是把被接收工件的最大完工时间与所有被拒绝工件总的拒绝费用之和最小化．对于在线情形，他们给出了一个在线算法，并且证明了这个在线算法有最好的竞争比2．618；对于离线情形，他们给出了一个近似比为2－的近似算法和一个多项式时间近似方案（这里m是平行机机器数量）［1］．自此以后，带有拒绝费用的工件排序问题受到越来越多的关注．对上述的工件在线排序问题，在所有的工件加工允许被中断的情况下，Seiden S给出了一个竞争比约为2．387 4的在线算法［2］．Hoogeveen H等人考虑了允许加工中断的工件离线排序问题，他们证明了这个问题是NP－困难的，并给出了一个全多项式时间近似方案［3］．Engles D W等人考虑了工件可拒绝的单机排序问题，目标是把被接收工件总的完工时间与所有被拒绝工件总的拒绝费用之和最小化；他们证明了这个问题是NP－困难的，并给出了一个全多项式时间近似方案［4］．Epstein L等人考虑了具有单位长度的工件的单机在线排序问题，目标是把被接收工件总的完工时间与所有被拒绝工件总的拒绝费用之和最小化，他们给出了一个竞争比约为1．866的在线算法，并且证明了任何确定的在线算法的竞争比至少为1．637 84［5］．Lu L F等人也对带有拒绝费用的工件排序问题做了大量的研究，对不同的机器环境进行了分析和探讨，并且得出了一系列结论［6－9］．

对工业生产中带有拒绝费用的工件排序问题，还有大量的挑战性的问题有待解决．本文研究了这一领域中的一个排序问题，探讨了它的计算复杂性，并且设计了一个动态规划算法．

1 排序问题的描述

对本文所考虑的带有拒绝费用的工件排序问题描述如下：

有1台机器，n个待加工的工件J1，…，Jn．并且每个工件Jj有一个加工时间pj和一个拒绝费用wj．工件Jj或者被拒绝并且支付一个确定的拒绝费用wj，或者被接收并安排在机器上加工．目标是使被接收工件总的完工时间与所有被拒绝工件总的拒绝费用之和达到最小．

2 排序问题的记号与概念

我们定义A和R分别为所有被接收工件的集合和所有被拒绝工件的集合．采用Graham P L等人提出的排序问题的一般记号［10］，把这个问题记为

根据1979年Graham P L等人提出的工件排序问题的三参数表示法［10］，我们使用α｜β｜γ来表示一个排序问题．在这里，α域表示机器的数量、类型和环境；β域表示工件的特征和约束；γ域表示要优化的目标．在本文中，α域、β域和γ域中的参数分别表示如下：

（1）α域：1表示单机，并且一次只能加工一个工件．

（2）β域：J1，…，Jn表示n个需要加工的工件；pj表示工件Jj的加工时间；wj表示工件Jj的拒绝费用；reject表示工件允许被拒绝且每个被拒绝的工件要支付一个拒绝费用wj．

（3）γ域：Cj表示工件Jj的完工时间，表示

j被接收工件总的完工时间；wj表示被拒绝工件Jj的拒绝费用，表示被拒绝工作总的拒绝用费；表示被接收工件总的完工时间与被拒绝工件总的拒绝费用之和．

3 排序问题的求解

针对所研究的排序问题，我们将设计一个动态规划算法来解决．

3．1 动态规划算法的思想

（1）动态规划方法的关键在于正确地写出基本的递推关系式和恰当的边界条件．要做到这一点，必须先将问题的过程分成几个相互联系的阶段，恰当地选取状态变量和决策变量及定义最优值函数，从而把一个大问题转化成一组同类型的子问题，然后逐个求解．即从边界条件开始，逐段递推寻优．在对每一个子问题的求解中，均利用了它前面的子问题的最优化结果，依次进行，对最后一个子问题求解所得到的最优解就是整个问题的最优解．

（2）在多阶段决策过程中，动态规划方法是既把当前一阶段和未来各阶段分开，又把当前效益和未来效益结合起来考虑的一种最优化方法．因此，每阶段的决策是从全局来考虑的，与单独考虑本阶段状态得出的决策一般是不同的．

（3）在求整个问题的最优策略时，由于初始状态是已知的，而每阶段的决策都是该阶段状态的函数，故最优策略所经过的各阶段状态便可逐次变换得到，从而确定最优路线．

3．2 动态规划算法

根据引理1，对工件重新标号，使得p1≤…≤pn．下面给出一个定理，在这个定理中，工件的最优加工次序与引理①中的工件的最优加工次序有密切的关系

定理1：在O（n2）时间内能得到问题的最优解．

对定理1证明如下：

设f（j，m）是所考虑工件为Jj，…，Jn且被拒绝工件的个数为m时所对应的最优目标函数值．

现在，考虑工件为Jj，…，Jn且被拒绝工件的个数为m时的一个最优排序．在这个排序中，仅仅有下面两种可能的情形：

情形1：工件Jj被拒绝并且支付一个确定的拒绝费用wj．

由于工件Jj被拒绝，则对于工件集Jj－1，…，Jn，所有被拒绝工件的个数为m－1，工件Jj对目标函数的贡献是wj，因此，有f（j，m）＝f（j－1，m－1）＋wj．

情形2：工件Jj被接收并安排在机器上加工．

由于工件Jj被接收，则对于工件集Jj－1，…，Jn，所有被拒绝工件的个数为m，工件Jj对目标函数的贡献是pj，因此，有f（j，m）＝f（j－1，m）＋pj．

综合上述两种情形，给出下面的动态规划算法DP．这种算法为：

（1）边界条件：

f（1，0）＝pj，f（1，1）＝wj；且在m≠0，1时，f（1，m）＝∞．

（2）递推函数：

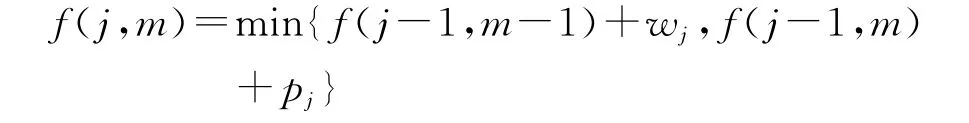
（3）最优值：

min｛f（n，m），1≤m≤n｝

由于1≤j≤n，且1≤m≤n，至多有O（n2）个不同的状态变量．并且每次迭代均花费一个常数时间．因此，动态规划算法DP的时间复杂性为O（n2），即可以在O（n2）时间内得出问题的最优解．

4 结 语

本文研究了工业生产中一个带有拒绝费用的排序问题，对该问题设计了一个动态规划算法，探讨了它的计算复杂性．这对于帮助决策者在加工产品时取舍工件提供了理论依据．

［1］Bartal Y，Leonardi S，Spaccamela A M，eta l．Multiprocessor Scheduling with Rejection［J］．SIAM Journal on Discrete Mathematics，2000，13：64－78．

［2］Seiden S．Preemptive Multiprocessor Scheduling with Rejection［J］．Theoretical Computer Science，2001，262：437－458．

［3］Hoogeveen H，Skutella M，Woeginger G J．Preemptive Scheduling with Rejection［J］．Mathematics Programming，2003，94：361－374．

［4］Engels D W，Karger D R，Kolliopoulos S G，eta l．Techniques for Scheduling with Rejection［J］．Journal of Algorithms，2003，49：175－191．

［5］Epstein L，Noga J，Woeginger G J．On－line Scheduling of Unit Time Jobs with Rejection：Minimizing the Total Completion Time［J］．Operations Research Letters，2002，30：415－420．

［6］Lu L F，Zhang L Q，Yuan J J．The Unbounded Parallel Batch Machine Scheduling with Release Dates and Rejection to Minimize Makespan［J］．Theoretical Computer Science，2008，396：283－289．

［7］Lu L F，Cheng T C E，Yuan J J，eta l．Bounded Single－machine Parallel－batch Scheduling with Release Dates and Rejection［J］．Computers and Operation Research，2009，36：2748－2751．

［8］Zhang L Q，Lu L F，Yuan J J．Single Machine Scheduling with Release Dates and Rejection［J］．European Journal of Operational Research，2009，198：975－978．

［9］Zhang L Q，Lu L F，Yuan J J．Single－machine Scheduling under the Job Rejection Constraint［J］．Theoretical Computer Science，2010，411：1877－1882．

［10］Graham P L，Lawler E L，Lenstra J K，eta l．Optimization and Approximation in Deterministic Machine Scheduling：A survey［J］．Annals of Discrete Mathematics，1979，5：287－326．

［11］Baker K R．Introduction to Sequencing and Scheduling［M］．New York：John Wiley ＆Sons，1979．

Study on the Scheudling Problem with Rejiction Cost in Industrial Production

FENG Qi，YANG Li－hua
（Zhongyuan University of Technology，Zhengzhou 450007，China）

In industrial production，decision－makers either accept a job or reject a job to obtain the maximum profit．In order to solve the problem which jobs should be accepted and which jobs should be rejected，a scheduling problem with rejection cost in industrial production in this paper is researched．A dynamic programming algorithm for the problem is designed．

scheduling；rejection；dynamic programming algoriathm

O223

A

10．3969／j．issn．1671－6906．2011．05．001

1671－6906（2011）05－0001－03

2011－09－15

国家自然科学基金项目（10971201；61070229）

冯 琪（1975－），女，河南周口人，讲师，博士生．