基于BLT方程的传输线网络电磁脉冲响应分析

李许东，王庆国，周 星，高永生

（军械工程学院静电与电磁防护研究所，河北石家庄 050003）

基于BLT方程的传输线网络电磁脉冲响应分析

李许东，王庆国，周 星，高永生

（军械工程学院静电与电磁防护研究所，河北石家庄 050003）

在介绍电磁拓扑理论的基础上，分析了频域传输线网络BLT超矩阵方程及各个参量的含义，并结合一种典型的环形传输线网络进行了分析，建立了该网络的拓扑模型及BLT方程，仿真分析了在某一结点注入干扰源时传输线网络中不同结点的频率响应，并结合傅里叶变换，研究了在不同位置、注入不同个数的脉冲干扰源时，传输线网络中结点的响应。

电磁拓扑；BLT方程；传输线网络；散射矩阵；电磁脉冲

现代社会中，商贸大楼、通信站、政府机关的办公楼等都分布着各种电子设备，以及大量的数据通信、语音通信、输电线路等传输线路，并形成分布式传输网络。这些传输线网络及其连接的各种使用终端（电话、计算机、通信设施等）分布密度高，大多都工作在高频、低压状态，对电磁骚扰极为敏感，是电磁易感源。

同时随着电子技术的发展，高功率微波、超宽带等电磁脉冲（EMP）设备不断趋向小型化，且更易于生产，价格也比较便宜，这种设备已经成为恐怖主义分子或战场敌方对政府机关、重要设施、武器系统和军事指挥机关进行袭击的一种手段。据美国国防部AD报告预测，EMP武器将是近年最有可能和最具有潜在价值的攻击武器［1］。目前这方面的研究工作主要集中在电磁脉冲对电子系统的直接辐射耦合的研究，而忽视了通过各种传输线网络进行传导耦合的研究，因此，研究电磁脉冲在典型传输线网络中的传导耦合规律有重要意义。本文主要运用电磁拓扑理论中的传输线网络BLT超矩阵方程，分析了一种环形结构传输线网络在集总激励源作用下的响应，并对结果进行了验证。

1 电磁拓扑理论及传输线网络BLT超矩阵方程

电磁拓扑学是电磁场理论与数学上的拓扑理论相结合而形成的一门交叉学科。它利用拓扑的概念将一个复杂的电子系统进行分解，从而降低整个系统分析的复杂性。它的基本思想是将研究对象分解成不同大小的区域，各个区域之间通过系统的拓扑图相联系，这样就可以把整个复杂的电磁耦合问题分解成一组相对独立的小的电磁问题来解决。对于外部电磁场通过电子系统外部的电源线、信号线或其他外露的导线引入系统内部形成的干扰，电磁拓扑理论通过结点和管道的二元关系建立网络的拓扑结构，并利用BLT方程进行分析［2－4］。早在20世纪70年代美国空军武器实验室的BAUM就首次提出电磁拓扑的概念，随后又与LIU和TESCHE一起基于合成电压波原理，将相对某一结点的入射分量和反射分量用传输线一维坐标的始点和终点电量来表示，推导出了电磁拓扑理论的著名方程——BLT方程，为人们提供了一套系统分析的理论工具［5－8］。

频域上传输线网络BLT超矩阵方程为

2 典型网络的电磁脉冲响应计算

2.1 模型的建立及参数设置

研究管道中仅含一根导线的传输线网络响应，其结构如图1所示（各导线均由转接头连接，结点3为一个三通转接头），管道、结点及导线上电磁波的传播情况如图2。管道T1—T6的长度L均设为2 m，特性阻抗均设为50Ω，结点6接一个对地匹配阻值为50Ω的负载，为了方便计算其余结点不加负载。在管道T6的中点处加一个幅度为1 V的电压激励源VS。

图2 脉冲信号传播拓扑图

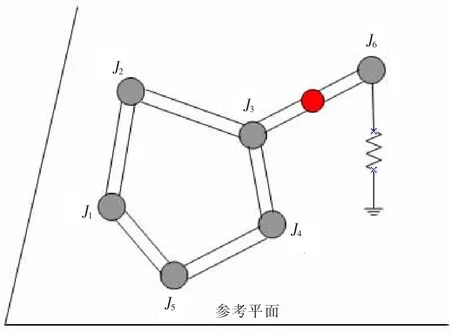
图1 环形传输线网络电磁拓扑图

2.2 环形网络BLT方程中矩阵求解

2.2.1 散射矩阵

传输线组成网络后，不仅需要考虑延时和反射，还需要考虑在传输线网络结点上反射时的传播特性，这里用散射超矩阵表示，具体推导见文献［5］，为计算方便，假设各个导线的特性阻抗相同，这样根据网络的散射特征参数矩阵，将各结点的散射矩阵值代入即可得到整个网络的散射矩阵。

2.2.2 传播矩阵

其中ΓTn为各个管道的传播矩阵；

由于各管道具有相同的长度（L＝2 m）和特性阻抗（50Ω），我们可以得到该网络的传播矩阵

2.3 频域仿真结果

根据上述情况运用BLT方程就可得到图1环形传输线网络中各结点上的实际电压、电流。图3—图6为加不同频率的激励源时不同结点处的频率响应曲线。

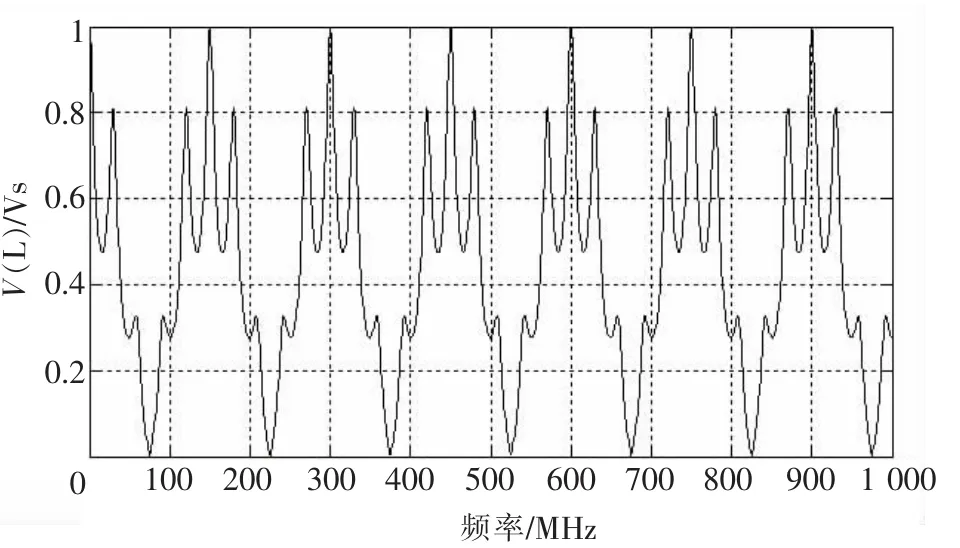
图3 传输线网络中的电压频域响应

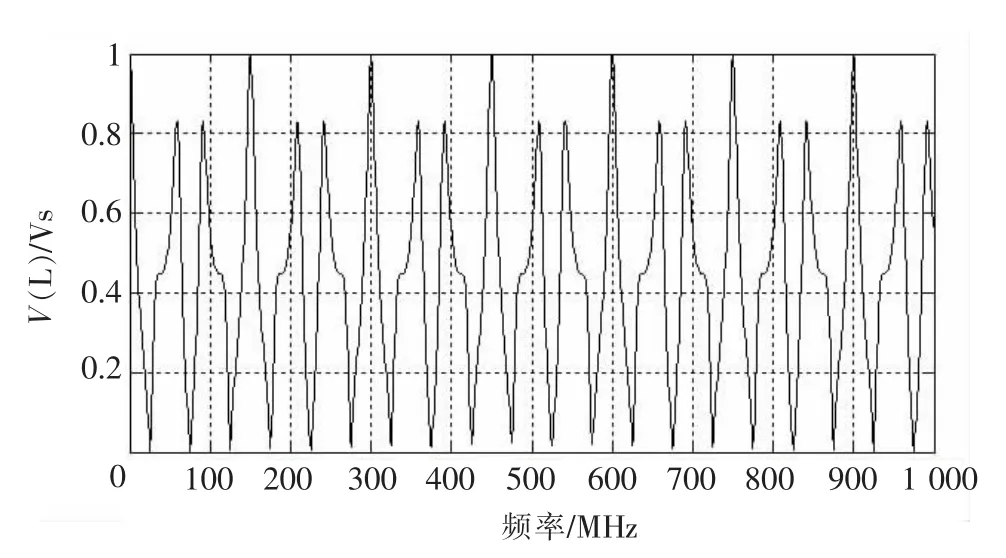
图4 传输线网络中的电压频域响应

图5 传输线网络中的电压频域响应

图6 传输线网络中的电压频域响应

从以上图中可以看出，由于环形结构和管道T6中存在振荡，所以在频率为30 MHz的倍数的位置上有不同幅值的峰值出现。通过计算可知，波在环形网络中传播1周的周期是33.33 ns，其频率是30 MHz，而峰值频率首次出现的位置也是30 MHz。结点J1和结点J5、结点J2和结点J4的频域响应相同，这是由于它们在网络结构中正好处于对称结构。管道T6一端接50Ω的匹配负载，因此该管道中没有反射分量，但是由结点J3的散射矩阵看出，波在该处会有反射现象，导致网络中形成了去波和来波。

2.4 时域仿真结果

若加的激励源为脉冲源，那么必须计算不同结点的时域响应波形。对于脉冲激励源，可以将脉冲源进行傅立叶变换，根据网络的频域仿真结果计算出脉冲激励源在频域上的响应，然后再反傅立叶变换计算它的时域响应。

运用双指数脉冲源，为看出波在传输线网络中的传播过程，给出波形的前沿较陡、后沿较平缓，其表达式是：

其波形如图7所示，根据网络的特征，激励源信号沿2个不同路径到达各结点时存在时间差，那么它们互相叠加就形成了结点上的实际响应波形，此规律可以用来检验计算程序的正确性。

下面将激励源从管道T6换到管道T5中点以及在管道T5和T6都加入激励源，则结点J2的电压瞬时响应波形如图8所示。

图8 激励源在不同位置时结点J 2的电压瞬时响应

图7 注入脉冲源波形

从上图可以看出，当管道T5和T6都有激励源时，根据叠加原理，结点J2的电压瞬时响应波形是激励源单独存在时的响应波形的叠加，这就验证了计算程序的正确性。

3 结 论

本文主要运用电磁拓扑理论中的BLT超矩阵方程对一个简单的环形结构传输线网络的电磁脉冲响应进行了分析。通过仿真计算可以看出，当外部电磁场作用于传输线网络某一段时，网络中各部分不可避免地受到影响。这为下一步实验验证打好了理论基础，另外，还有常见的星形网、树形网等结构更复杂的网络及多导体网络有待进一步研究。电磁拓扑理论中的BLT方程不仅在分析传输线网络时具有很大的优势，是研究传输线网络电磁耦合问题的重要工具，还在复杂系统电磁兼容分析和电磁干扰研究方面有广泛的应用。

［1］ MILLER，COLIIN R.Electromagnetic Pulse Threats in 2010［R］.［S.l.］：［s.n.］，2005.

［2］ 安 霆，刘尚合.基于BLT方程的电磁干扰建模［J］.高电压技术，2007，33（12）：55-58.

［3］ 翁凌雯，牛忠霞，林竞羽，等.运用BLT方程研究高功率微波的电磁干扰［J］.强激光与粒子束，2005，17（8）：1 272-1 276.

［4］ 林竞羽，周东方，毛天鹏，等.电磁拓扑分析中的BL T 方程及其应用［J］.信息工程大学学报，2004，5（2）：118-121.

［5］ 谢彦召.架空线缆和线缆网络的电磁脉冲响应研究［D］.北京：清华大学，2005.

［6］ BAUM C E，LIU T K，TESCHE F M.On the analysis of general multiconductor transmission-line network［Z］.［S.l.］：［s.n.］，1978.

［7］ BAUM C E，Extension of the BLT equation［Z］.［S.l.］：［s.n.］，1999.

［8］ FREDERICK M.Tesche.Development and use of the BLT equation in the time domain as applied to a coaxial cable［J］.IEEE Transactions on Electromagnetic Compatibility，2007，49（1）：3-11.

TM15

A

1008-1542（2011）07-0183-04

2011-06-20；责任编辑:王海云

国家自然科学基金（50977091）

李许东（1984-），男，山西闻喜人，硕士研究生，主要从事电磁环境模拟与防护技术方面的研究。