超塑性成形/扩散连接空心结构设计和强度分析
2011-12-26刘鹏程陈建平
刘鹏程,陈建平,王 斌
(1.天津科技大学机械工程学院,天津 300222;2.航天特种材料及工艺技术研究所,北京100074)
超塑性成形/扩散连接空心结构设计和强度分析
刘鹏程1,陈建平1,王 斌2
(1.天津科技大学机械工程学院,天津 300222;2.航天特种材料及工艺技术研究所,北京100074)
为研究超塑性成形/扩散连接组合工艺制备的钛合金四层结构中芯层结构、芯层和蒙皮的扩散连接面积比率及芯层之间的扩散连接率对结构强度、刚度的影响规律,采用FEM分析了不同芯层结构、直筋数量及工艺参数条件下的多层结构零件强度、刚度变化规律,并重点研究了0.5 H/L和延伸率等关键因素的最佳取值区间。结果表明:超塑性成形/扩散连接四层结构件的芯层结构设计对强度和刚度影响较大,控制0.5 H/L值及芯层延伸率,可以使强度刚度均达到最高,最大限度地发挥四层结构的整体优势。同时,两相邻芯层在胀起时形成的圆角半径大小对芯层之间及芯层和蒙皮的扩散连接焊合率有很大影响,进而影响多层结构的强度和刚度。
超塑性成形;扩散连接;扩散连接率;芯层结构
传统飞行器结构件采用铆接、螺接、胶接和焊接等方法将许多“片片”、“条条”和“块块”连接起来,成为完整的结构件,这些结构件通常由几个或几十个,甚至几百个零件组成,因而制造周期长、手工劳动量大、成本高。利用超塑性成形/扩散连接组合工艺制造的复杂结构,其整体性强、结构强度高、刚性大且重量轻,是典型的轻量化整体结构[1-3]。现已分别研制出单层板的口盖,双层板的舱门等大量结构件。而在航空航天领域应用最为广泛的是三层和四层结构,这种结构充分发挥了钛合金材料超塑性和扩散连接性能优势和工艺一体化特性,具有制造成本低,成形件结构重量轻等优点,与传统钢结构相比,可以减重约20%~40%,降低制造成本约20%~50%[4-7]。美国在20世纪80年代中期为T38飞机制造了三层结构的主起落架舱门,英国IEP公司为A310,A320飞机研制的机翼维护口盖以及法国达索公司生产的缝翼都采用了四层结构[1]。
笔者研究的钛合金四层结构主要作为翼类零件使用,用钛合金板材超塑性成形/扩散连接组合工艺制备而成,其结构形式如图1所示。作为舵翼结构件使用,该结构必须能够承受抗弯、抗冲击、抗热震颤等外界作用。而对于四层超塑性成形/扩散连接结构,影响其强度、刚度因素来自2方面:其一是设计时已经确定的,即强度、刚度取决与采用什么样的芯层结构;其二是由成形工艺决定的,成形工艺中影响强度的主要因素是芯层和蒙皮的扩散连接面积比率,芯层之间的扩散连接率。笔者主要是通过有限元结构强度计算,分析结构设计与芯层和蒙皮的扩散连接比率对结构强度、刚度的影响。

图1 超塑性成形/扩散连接多层结构试验件Fig.1 Specimen of superplastic and diffusion bongding
1 超塑性成形/扩散连接工艺介绍及术语描述
四层结构超塑性成形/扩散连接工艺可分为2个步骤,先是内层的扩散连接,同时外层的超塑性成形,然后是内层超塑性成形以及内层和外层的扩散连接,其工艺过程:坯料制备—坯料表面处理—制备芯层结构—封焊—进炉加热升温—外层进气—内层进气,如图2所示。
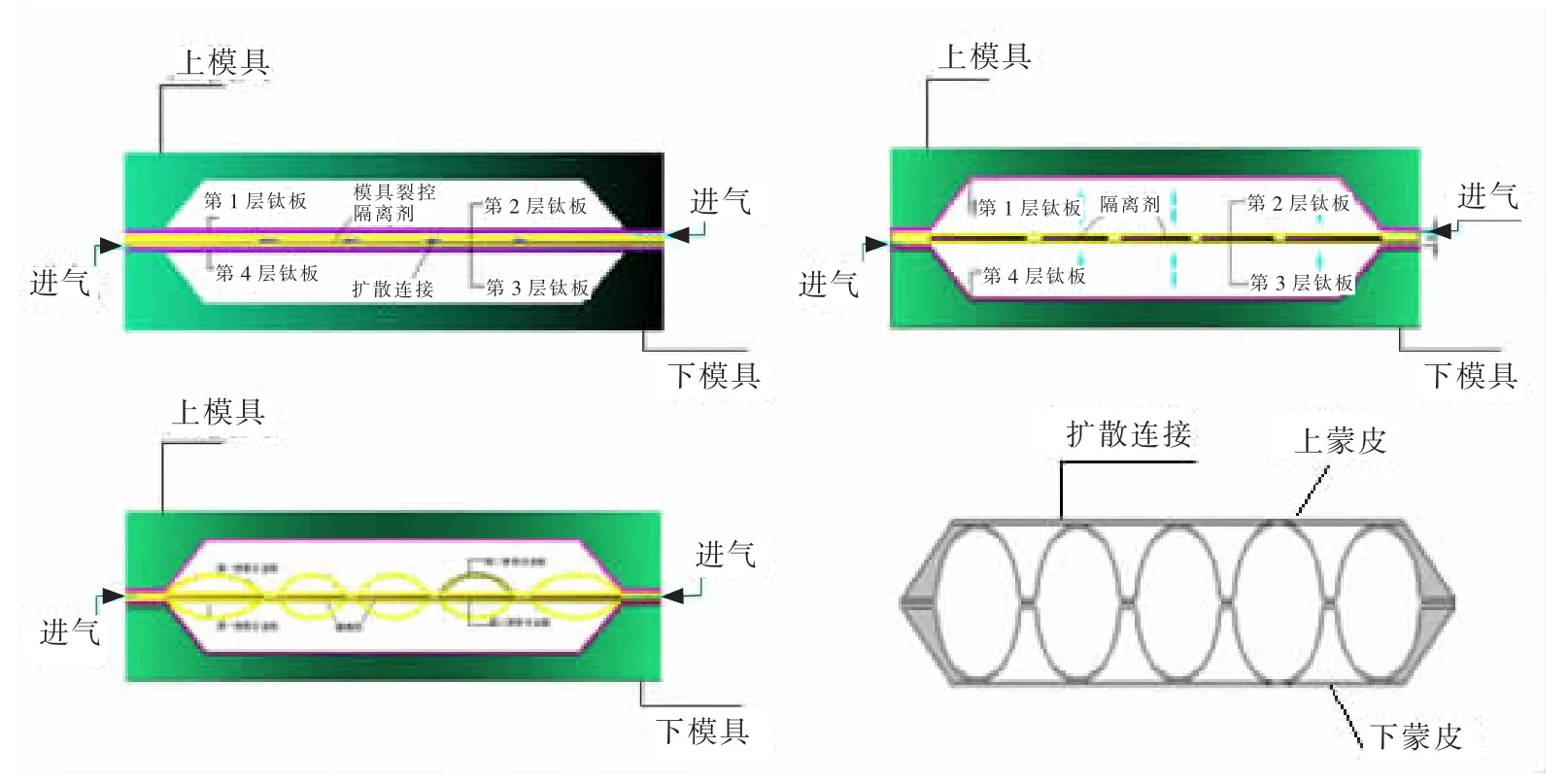
图2 成形工艺原理图Fig.2 Principle of superplaseic and diffusion bongding processing
本文所涉及术语描述如下:扩散连接面积率是指蒙皮和芯层已扩散部分面积和总面积的比值;芯层是指四层结构的中间2层;蒙皮是指四层结构的外面2层板(如图2所示);横筋是指相当于传统蒙皮骨架结构的翼肋,平行于弹身轴线(x方向)(如图3所示);直筋是指相当于传统蒙皮骨架结构的翼梁,一般垂直于弹身轴线或成放射状(如图3所示)。
2 芯层结构形式对强度影响
在零件要求总质量一定情况下,对板材厚度的选择也基本确定,板厚一定时,采用什么样的芯层结构以及排布形式对结构强度、刚度影响很大,目前常采用的结构有直泡结构,密集方泡结构,六边形蜂窝结构等。
在抗弯状态下翼梁(直筋)主要传递y方向的弯矩,翼肋并不传递y方向的弯矩,因此翼类零件的整体抗弯强度和刚度主要取决于直筋的排布[2],笔者仅就直筋的设计来对结构强度和刚度进行模拟。从传统结构力学分析,希望直筋的数目越多越好,直筋数目越多其支撑效果越好,其强度和刚度越高。然而,由于超塑性成形/扩散连接工艺的特殊性,成形过程中其芯层在超塑性成形时由于拉伸变形而厚度变薄。从成形工艺考虑当直筋数目越多,芯层变形量越大,减薄也就越厉害,容易在芯层超塑性成形时吹破,因此必须设计合理的直筋数目,使得成形时芯层不至于超出其变形极限。从材料力学角度考虑,由于芯层减薄,使得s值、w值都减小,不利于承力,如图4所示。因此,直筋数目越多并不一定提高结构强度和刚度,所以对于超塑性成形/扩散连接结构件不能一味追求支撑筋的数目来提高强度和刚度。

图3 四层结构的芯层示意图Fig.3 Core sketch of superplastic forming/diffusion bonding structure
在零件总宽度和总高度一定时,H为一定值,直筋数目随L值变化,L越大,直筋数目越少。在零件高度一定时,s1的值是恒定的,s的大小主要取决与s2,s2又取决于芯层的变形减薄程度,s2减小导致s值减小,整个承力结构件的蒙皮承力厚度减小,反而不利于强度和刚度提高。因此,直筋数量增加和s的减小是一对矛盾,必须设计合理的芯层结构使得0.5 H/L得到最佳比例,才能发挥四层结构强度和刚度的优势。有限元数值模拟在航空航天工业的板料超塑性成形中应用广泛[8],与工艺实验相比,它不仅节约费用,而且能提供直接的信息和引导,从而减少实验的次数,有时甚至能越过试探性的实验[9-11]。有限元数值模拟已经成为超塑性成形工艺设计中减少工艺开发时间、改善工件成形质量的非常必要的方法[12-14]。通过有限元数值模拟来分析0.5 H/L最佳比值。
模拟计算中,设计零件总高度为60 mm,也就是H+2s2=60 mm,零件总长度、宽度均为400 mm,如图5所示。计算芯层减薄时假设芯层均匀减薄,不考虑芯层和蒙皮扩散连接时的摩擦影响,材料选用板厚为1.5 mm的BT20钛合金板材,其质量密度为4.45 kg/cm3,泊松比为0.34,弹性模量为118 GPa。
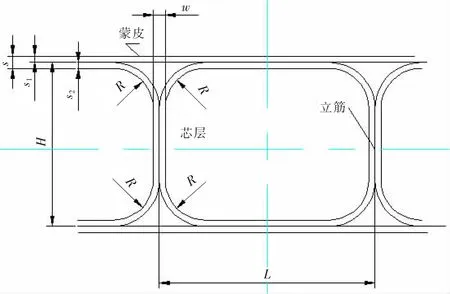
图4 四层结构内部示意图Fig.4 Inner sketch of four sheet SPF/DB structure
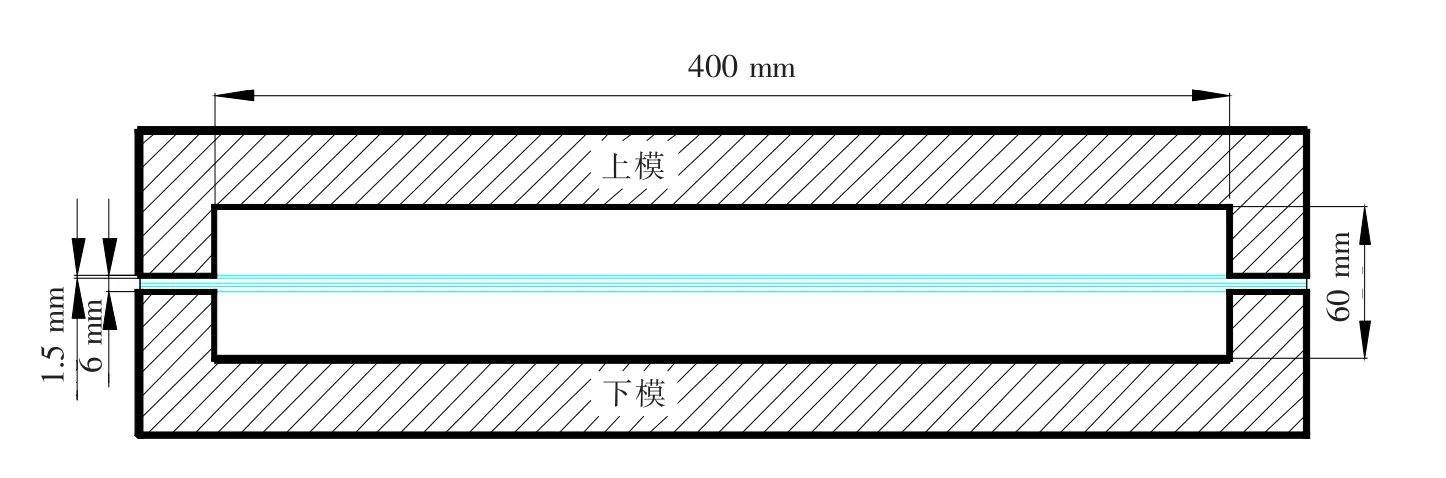
图5 模拟计算零件模具图Fig.5 Two dimension sketch of moding die
根据体积不变,可计算出蒙皮变形后的厚度为1.329 mm,芯层变薄需根据设计的直筋的数目来计算,分别设计直筋的数目为9,10,11,12,13,14,15,16,有限元分析时,在结构件的某面上施加1.0 MPa的均布压力,一端固定,类似悬臂梁结构,节点数为11 185个,网格数目为1 752个。
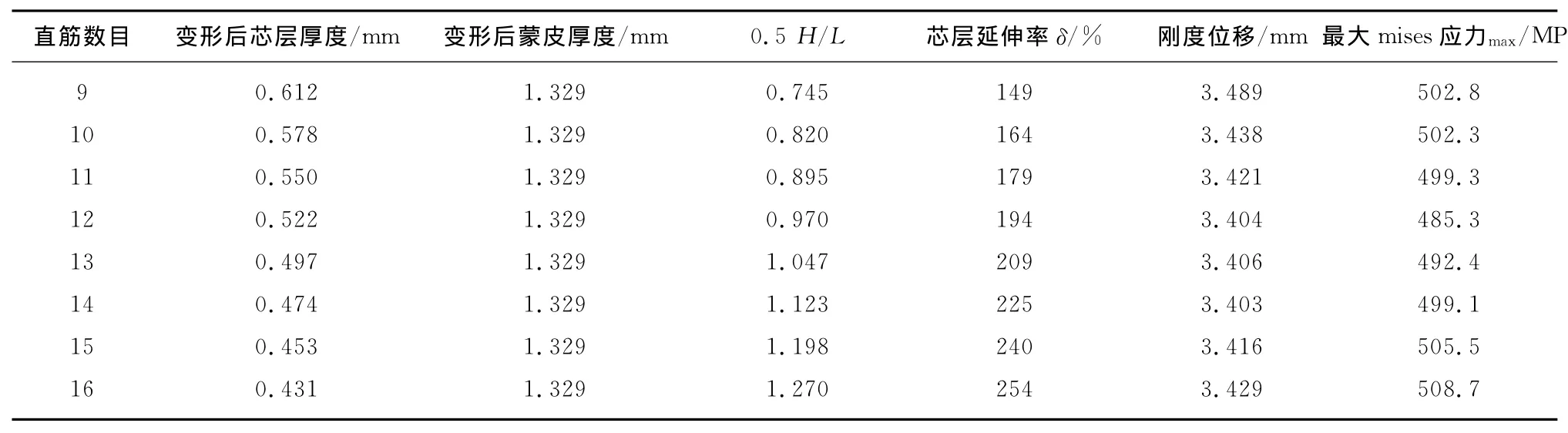
表1 不同芯层结构的芯层板厚变化及有限元分析结果Tab.1 Result of FEM for different thickness according to different core struture
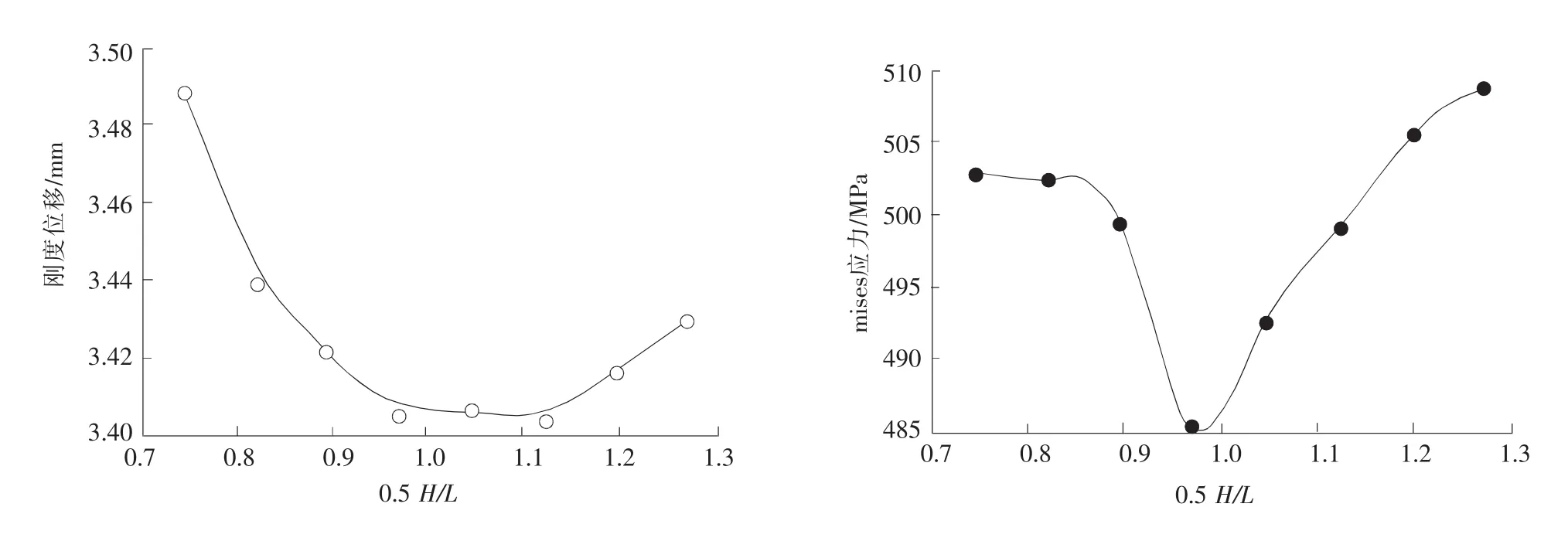
图6 0.5 H/L-刚度位移和mises应力曲线Fig.6 Curve on 0.5 H/L-stiff displacement and mises stress
计算结果如表1所示,图6为刚度变化趋势曲线。从图6和表1可看出在0.5 H/L接近于1,芯层延伸率为200%左右时,才能最好发挥四层结构强度和刚度综合优势。为了验证以上结果是否能作为一般规律,设计了其他结构形式,分别近似取0.5 H/L为0.8,1.0和1.2,零件尺寸为300 mm×300 mm×40 mm,芯层和蒙皮均采用板材厚度选用1.2 mm的钛合金,加载方式和前面相同。通过计算,蒙皮厚度变形为1.073 mm,0.5 H值为18.963,考虑的芯层泡为整数,分别设计为11,15,18根直筋,不同芯层结构变形规律如表2所示。结果证明,在0.5 H/L接近于1,芯层延伸率为200%左右时 ,四层结构件强度、刚度均达到最高,是最理想的组合。

表2 不同芯层结构模拟结果Tab.2 Result of different structure
对于以上结果可从材料力学角度加以分析,翼面在承受弯曲载荷时,可简化为悬臂梁,对于单根直筋可进一步简化为工字梁,其抗弯强度和刚度主要取决于抗弯截面模量,而抗弯截面模量取决于横截面积和高度。实际上,由于弯曲正应力沿截面高度按直线规律分布,当离中心轴最远处的正应力达到许用应力时,中性轴附近各点处的正应力仍很小,而且,由于其离中性轴近,力臂小,承担的弯矩也很小[2]。所以,将较多的材料放置在远离中性轴的部位,必然会提高材料的利用率,从这个角度考虑,在设计芯层时不能只追求直筋数目,因为直筋数目越多,芯层变薄越大,蒙皮处堆积的材料越少,不利于抗弯曲。
3 芯层和蒙皮扩散连接率对强度和刚度的影响
扩散连接面积的大小主要取决于芯层在超塑成形时圆角半径R的大小,圆角半径越大扩散连接面积越小,圆角半径越小,扩散连接面积越大,当R趋于零时,扩散连接面积趋于100%(如图7所示)。一般来说在超塑性成形过程中芯层和蒙皮贴合时圆角半径大小很难控制,尤其是对于指定的圆角半径,通过摸索工艺参数来控制圆角半径将很难做到,而且摸索工艺参数的试验成本非常昂贵。笔者旨在通过有限元数值模拟计算分析圆角半径对抗弯刚度和抗弯强度影响,并分析其影响规律。分析过程中取前面400 mm×60 mm零件进行分析,板材厚度为1.5 mm,设计芯层结构为13个泡状结构,变形后蒙皮厚度为1.329 mm,芯层厚度可根据圆角半径大小计算,计算结果如表3,关系曲线图8所示。
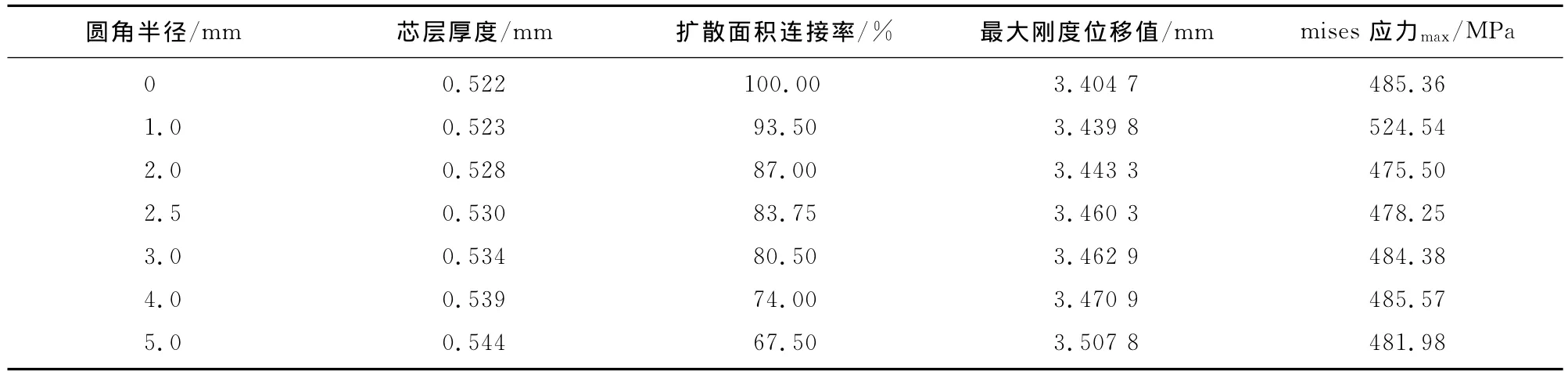
表3 扩散连接率和强度、刚度对应关系Tab.3 Effect of diffusion bonding area ration on mises stress and stiff
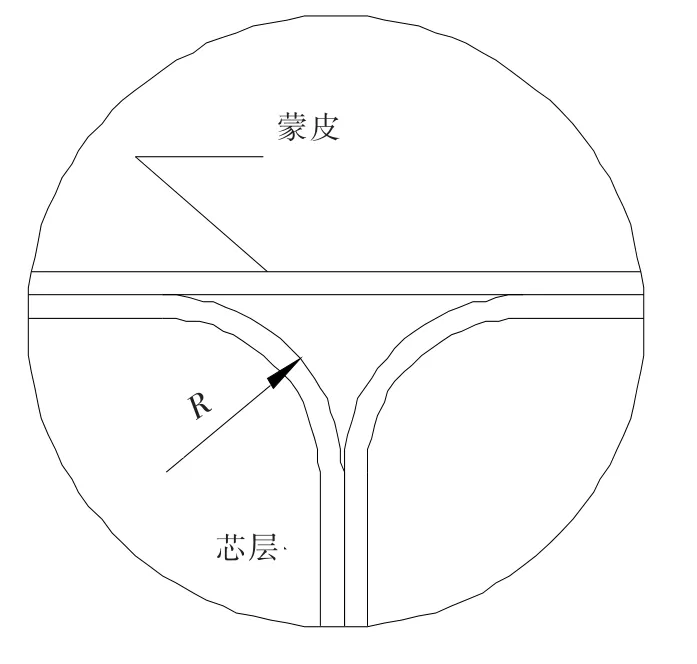
图7 圆角半径大小对强度影响Fig.7 Effect on the radius of core sheet
由以上分析可看出随着扩散连接面积率升高,刚度有升高的趋势,但刚度的变化不明显,而通过mises应力反应出来的强度指标并不表现出相同的规律,其强度值在扩散连接面积率为85%左右时最高,在扩散连接面积率100%时,其刚度值最高,其mises应力并不是最小,而是随扩散连接面积率先增加后减小,在85%左右mises应力值最小。综合考虑mises应力和刚度位移因素,控制扩散连接面积率在85%左右时比较合适。在成形工艺过程中,控制圆角半径大小十分困难,通过摸索工艺参数来控制扩散连接面积率时成本也很难实现,成本也会很高。以上分析并不是为在工艺中如何控制参数而达到控制扩散连接面积率的目的,而是为超塑性成形/扩散连接四层结构件的无损检测提供判据,四层结构超塑性成形/扩散连接结构件芯层和蒙皮扩散连接的无损检测是产品交付前必须检测的项目,芯层和蒙皮扩散面积率检测一般用超声反射法,其检测图片中焊合区和未焊合区灰度有明显差别,未焊合区出现在图7所示的圆角半径区,在超声检测时形成灰度较浅的区域,如图9所示。因此,在制定芯层和蒙皮扩散连接检测标准或规范时可认为扩散连接面积率达到85%,就认为该项目检测合格。
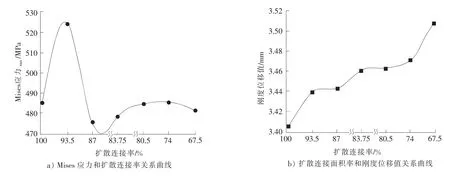
图8 扩散连接面积率和强度刚度关系Fig.8 Effect of diffusion bonding area ration on mises strees and stif
通过设计和计算其他结构验证上述研究结果,其计算结果和上述结论一致。分析原因可能是由于两圆角形成的支撑作用,而且圆角可减小应力集中,提高了整体结构强度。当圆角半径太小容易导致应力集中,圆角半径太大,扩散连接面积不够,中间加强筋支撑效果不明显,所以其强度也降低。而刚度值主要受截面形状影响,扩散连接面积越大,蒙皮处集中材料越多,蒙皮整体性越好,所以其刚度值随扩散连接面积率增大而增大。
4 结 论
1)超塑性成形/扩散连接四层结构件其芯层结构设计对强度和刚度影响较大,控制0.5 H/L接近于1,芯层延伸率为200%左右时,四层结构件强度、刚度均达到最高,是最理想的组合,能最好发挥四层结构整体强度和刚度的优势。
2)超塑性成形/扩散连接四层结构在芯层超塑性成形时,两相邻芯层在胀起时必定会形成圆角,圆角半径大小影响着扩散连接焊合率,从而影响强度和刚度,扩散连接面积率越高刚度越高,而其最大mises应力在扩散连接面积率为85%左右达到最低。
[1] YOON J H,LEE H S,YI Y M.Finite element simulation on superplastic blow forming of diffusion bonded 4 sheets[J].Journal of Materials Processing Technology,2008,201:68-72.
[2] HAN W B,ZHANG K F,WANG G F.Superplastic forming and diffusion bonding for honeycomb structure of Ti-6Al-4V alloy[J].Journal of Materials Processing Technology,2007,183:450-454.
[3] LEE H S,YOON J H,PARK C H,et al.A Study on diffusion bonding of superplastic Ti-6Al-4V ELI grade[J].Journal of Materials Processing Technology,2007,(187-188):526-529.
[4] LUTFULLIN R Y,KRUGLOV A A,SAFIULLIR V N,et al.Processing properities of nano-and submicro-crystalline Ti-6Al-4V titanium alloy[J].Materials Science and Engineering A,2009,503:52-54.
[5] LUO Y,LUCKEY S G,FRIEDMAN P A,et al.Development of an advanced superplastic forming process utilizing a mechanical preforming operation[J].International Journal of Machine Tools & Manufacture,2008,48:1 509-1 518.
[6] YOON J H,Lee H S,YI Y M ,et al.Prediction of blow forming profile of spherical titanium tank[J].Journal of Materials Processing Technology,2007,(187-188):463-466.
[7] ZHANG K F,WANG G F,WU D Z,et al.Reaearch on the controlling of the thickness distribution in superplastic forming[J].Journal of Materials Processing Technology,2004,151:54-57.
[8] CHUMACHENKO E N.Development of computer simulation of industrial superplastic sheet forming[J].Materials Science and Engineering A,2009,499:342-346.
[9] LI G Y,TAN M J,LIEW K M.Three-dimensional modeling and simulation of superplastic forming[J].Journal of Materials Processing Technology,2004,150:76-83.
[10] O’BRIEN M J,BREMENB H F,FURUKAWA M,et al.A finite element analysis of the superplastic forming of an aluminum alloy processed by ECAP[J].Materials Science and Engineering A,2007,456:236-242.
[11] CARRINO L,GIULIANO G,NAPOLITANO G.A posteriori optimisation of the forming pressure in superplastic forming processes by the finite element method[J].Finite Elements in Analysis and Design,2003,39:1 083-1 093.
[12] CARRINO L,GIULIANO G,PALMIERI C.On the optimisation of superplastic forming processes by the finite-element method[J].Journal of Materials Processing Technology,2003,(143-144):373-377.
[13] GIULIANO G.Simulation of instability during superplastic deformation using finite element method[J].Materials and Design,2005,26:373-376.
[14] XIANG Y B,WU S C.Numerical simulation of cavity damage evolution in superplastic bulging process[J].Journal of Materials Processing Technoloty,2001,116:224-230.
Design and strength analysis of superplastic forming/diffusion bonding hollow panel structure by FEM
LIU Peng-cheng1,CHEN Jian-ping1,WANG Bin2
(1.Mechanical Engineering College,Tianjin University of Science and Technology,Tianjin 300222,China;2.Aerospace Research Institute of Special Material and Processing Technology,Beijing 100074,China)
In order to study the influence of the structure of core sheet,the ratio of the diffusion bonding area between the core layer and cover layer,and the ratio of diffusion bonding area between core sheets on the strength of multi-layer structure fabricated by superplastic forming/diffusion bonding process,FEM is used to analyze the rigidity and strength of different parts with different structures of core sheet and process parameters.In the research emphasis is put on two critical factors:0.5 H/L and the elongation.The results show that the structure of core has greater influence on the rigidity and strength of multi-layer titanium hollow panel structure and the controlling of the value of 0.5 H/L and elongation can realize maximal rigidity and strength,which maximize the overall advantages of multi-layer structure.Meanwhile,the radius of corner between the two near core sheets have greater influence on the ratio of diffusion bonding area between core sheet and cover sheet and two near core sheets,thereby affecting the strength and rigidity of multi-layer structure.
superplastic forming;diffusion bonding;ratio of diffusion bonding;structure of core layers
TG146
A
1008-1542(2011)05-0435-06
2011-04-15;
2011-08-20;责任编辑:张 军
天津市2010年重点基金资助项目(10JCZDJC23300)
刘鹏程(1975-),男,天津人,助理工程师,硕士,主要从事机械制造及其自动化方面的研究。
