基于变尺度差商比序列统计量的小子样静态一致性检验
2011-12-26郝晋峰李经中
郝晋峰,郭 辉,李经中,王 琦,徐 成
(1.军械工程学院六系,河北石家庄 050003;2.河北科技大学外国语学院,河北石家庄 050018;3.66440部队,河北石家庄 050081;4.78636部队,四川什邡 618419)
基于变尺度差商比序列统计量的小子样静态一致性检验
郝晋峰1,郭 辉2,李经中1,王 琦3,徐 成4
(1.军械工程学院六系,河北石家庄 050003;2.河北科技大学外国语学院,河北石家庄 050018;3.66440部队,河北石家庄 050081;4.78636部队,四川什邡 618419)
针对小子样条件下静态一致性检验问题,介绍了利用次序统计量相关理论进行一致性检验的部分方法,在对此类方法的检验过程进行深入探讨的基础上,借鉴已有的部分研究结论,对利用变尺度差商比序列统计量进行一致性检验的思路和方法进行了改进,改进后的方法适用于任意分布子样,计算过程简便且检验效果良好。
小子样;一致性检验;秩和检验法;次序统计量;变尺度差商比序列统计量
武器装备试验和鉴定工作中,由于试验成本等客观条件的限制,完全依靠现场试验信息进行试验分析的方法已无法满足现实需求。随着仿真技术的日渐成熟,研究人员更加关注小子样条件下合理利用仿真数据进行科学统计决策的研究。由于数据是对实际情况的模拟,其结果可信性、与现场试验数据差异性,将直接影响到后续试验鉴定方法的合理运用,因此在利用仿真数据前,必须对其与现场试验数据的一致性进行验证,即一致性检验。
目前,针对一致性检验方法的讨论很多,方法研究也较为成熟,但适用于小子样情况下的检验方法还比较少。文献[1]对小子样条件下秩和检验法的应用进行了讨论,但秩和检验法适用范围相对较小,某些情况下检验精确度不甚理想。部分研究人员又提出了利用次序统计量的相关理论来解决一致性检验问题的方法[2],但其理论推导过程存在一定的缺陷,文献[3]对文献[2]中的方法进行了深入分析,指出了原有方法的缺陷,并提出了一系列利用变尺度差商比序列统计量进行一致性检验的方法,较好地解决了部分特定分布子样的一致性检验问题,但没有给出适用于任意分布的小子样一致性检验的思路和方法[4]。
笔者通过对秩和检验法和某正态分布数据一致性检验方法的进一步分析,并结合已有研究结论,给出了利用次序统计量构造变尺度差商比序列统计量对小子样条件下任意分布进行一致性检验的思路和方法。
1 一致性检验的基本方法和思路
1.1 基本方法
研究子样间一致性问题的方法有很多,比较成熟的定量方法为数理统计中假设检验的方法。设有2组样本(X1,X2,…,Xn)和(Y1,Y2,…,Yn),其分布函数为F(x)和G(y),验证2组子样的一致性就是要验证2组子样是否符合同一分布。根据试验背景的不同,大体有以下3种情况。
1)2组子样分布形式相同且已知,但分布参数未知。在工程试验中,根据以往经验有时可以提前预知2组子样的分布形式,但分布参数未知,此时可利用参数假设检验的方法来验证2组子样分布的分布参数相同,进一步得到一致性结论。
2)2组子样中,一组子样分布完全已知,另一组子样分布未知。假设分布G(y)完全已知,而F(x)未知,此时的一致性检验问题即转化为验证子样(X1,X2,…,Xn)服从分布G(y)的拟合优度检验问题。
3)2组子样分布的形式与参数均未知。此时可利用非参数假设检验对2组子样分布进行相等性检验。
1.2 基本思路
小子样情况指现场试验子样较少的情况,对仿真试验样本量没有特定要求,因此在处理小子样一致性检验问题时一般有2种基本思路:一种是利用自助法(Bootstrap)等方法对子样进行再抽样,将小子样转化为大子样问题,然后选取适合大子样的假设检验方法进行一致性检验;另一种则是直接选用适合小子样的方法进行,如W 检验、秩和检验等等。
2 小子样条件下一致性检验
在检验过程中利用经验分布函数对分布形式进行近似,以次序统计量为出发点构造相应统计量进行假设检验。

3 基于变尺度差商比序列统计量的一致性检验
文献[2]介绍了利用变尺度差商比序列统计量对任意分布进行一致性检验的基本思路,但该思路存在一定的理论缺陷[3],文献[4]提出了一系列利用变尺度差商比序列统计量进行一致性检验的方法,笔者以正态分布子样的检验方法为例,对其检验统计量分布的一般形式以及一般情况下该检验方法的运用进行深入探讨。
3.1 变尺度差商比序列统计量定义
假设存在2组子样(x1,x2,…,xn1)和(y1,y2,…,yn2),由小到大混合排序记为 X(1)≤X(2)≤…≤X(n1+n2),其中n1+n2=n,构造检验统计量,称其为变尺度差商比序列统计量[4]。利用该统计量进行的检验为一种多尺度分析,是以Xk-Xi为尺度测量Xj与Xi有无差异性。
3.2 相关分析
可以看出,上述检验方法对于不同的i,j,k取值,Xijk的分布函数非常难于求解,而且其分布函数不具有一般表达式,其临界值也只能通过大量模拟计算求得。在实际的工程试验鉴定中,此检验方法计算量过大,适用范围比较窄,只适用于n非常小的情况下正态分布数据的一致性检验问题。虽然文献[4]提出了一系列的检验方法,但这些方法均是针对某类分布的特定方法,不具有一般性。因此,有必要提出一种计算简便且适用于任意分布的基于变尺度差商比序列统计量的一致性检验思路和方法。
4 任意分布的变尺度差商比序列统计量检验
根据以上讨论,并借鉴文献[2]—文献[4]的相关结论,利用变尺度差商比序列统计量,给出任意分布下静态一致性检验的思路和方法。
4.1 基本原理

给定不同的α,以双侧检验为例,可设定P{Zijk<z1}=P{Zijk>z2}=α/2,查不完全β函数表或通过模拟计算可求得相应的z1,z2值。同时可看出ak的表达式即为次序统计量X(k)的分布函数,根据子样分布F(x)的不同,可分别求得ak的值,进一步可得到检验统计量Zijk的值。若z1<Zijk<z2,则αk符合U(0,1)均匀分布,2个子样相容;若Zijk≤z1或Zijk≥z2,则αk不符合U(0,1)均匀分布,2组子样不相容。
4.2 相关分析
1)上述方法适用于任意分布的一致性检验,并且在进行检验前子样所符合的总体分布F(X)需完全已知。在无法预知分布时,若仿真子样充足,则直接计算其经验分布Fn(X)用以近似F(X);若仿真子样也略显不足,则利用Bootstrap法对子样进行再抽样以获得足够的再生子样,利用再生子样计算经验分布(X)用以近似F(X),最后运用上述方法进行一致性检验。
2)利用上述方法进行一致性检验,需对所有αk构造的检验统计量Zijk进行逐一讨论,有1个不符合一致性条件则认定2个子样不相容。
3)上述方法是利用了变尺度差商比序列统计量对αk是否满足U(0,1)进行了检验,也可以利用拟合优度检验的方法检验αk是否满足U(0,1)。
5 算例分析
以标准正态分布U(0,1)为例,随机产生子样x1=1.066 8,x2=-0.095 6,x3=0.059 3,x4=0.294 4,x5=-0.832 3,利用4.1所述任意分布一致性检验方法进行检验。
将子样排序有次序统计量:x(1)=-0.832 3,x(2)=-0.095 6,x(3)=0.059 3,x(4)=0.294 4,x(5)=1.066 8。利用式(3)有α1=0.677 6,α2=0.761 3,α3=0.544 2,α4=0.364 8,α5=0.462 3,将αk排序并求得个检验统计量Zijk的值。
令α=0.05,设定P{Zijk<z1}=P{Zijk>z2}=α/2,利用 Matlab逆累计积分布函数计算可求得此时的拒绝域z1和z2的值,将Zijk与z1,z2同时列于表1。可以看出,对任意Zijk,均有z1<Zijk<z2,故子样满足一致性。
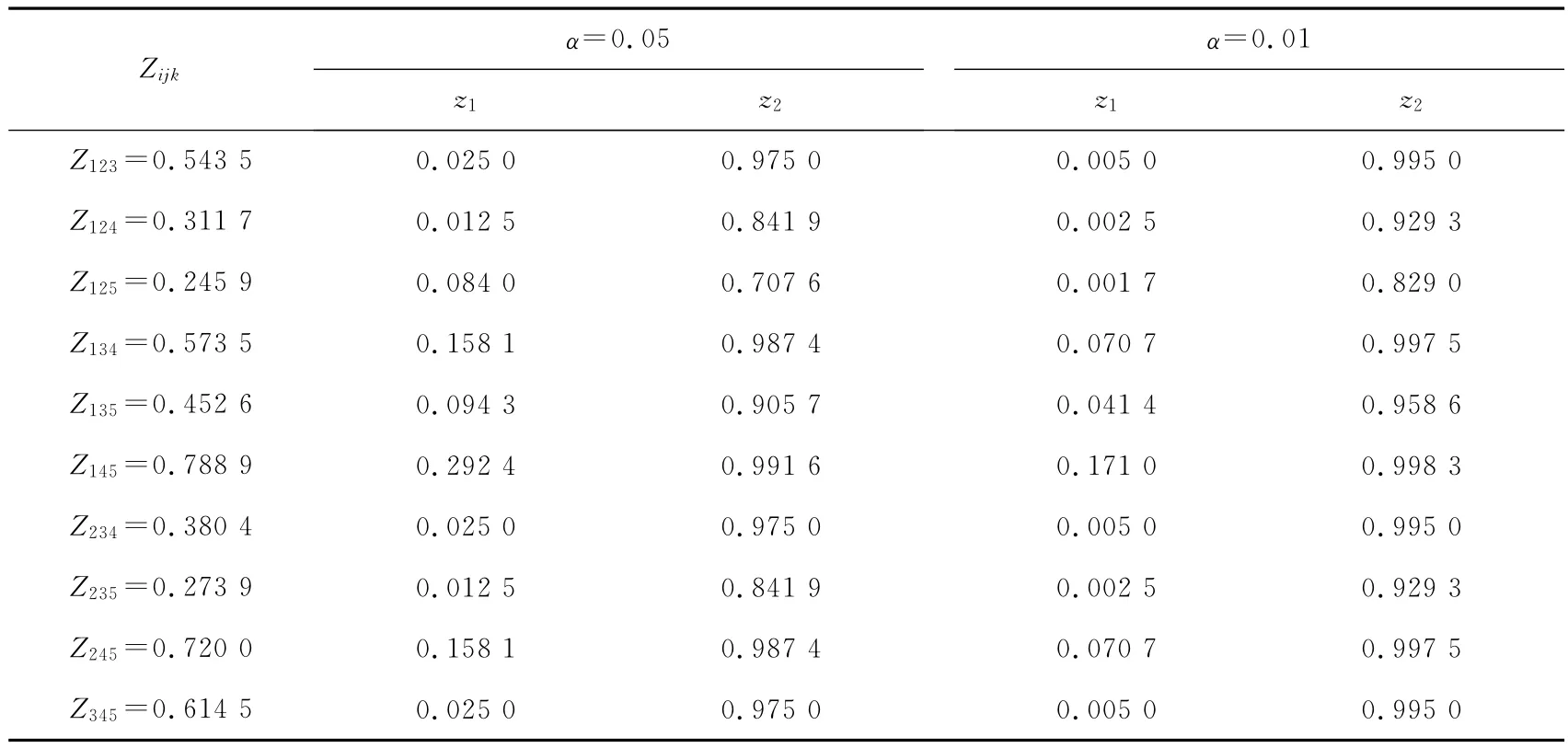
表1 n=5时,Zijk与z 1,z 2的取值Tab.1 Values of z 1,z2 and Zijk when n=5
6 结 语
笔者针对小子样条件下静态一致检验问题,介绍了利用次序统计量构造变尺度差商比序列统计量对任意分布小子样静态数据进行一致性检验的基本思路和方法,通过与已有检验方法的对比分析和实例验证得出,该方法检验统计量的分布形式确定且易于计算,适用于任意分布形式数据的一致性验证。
[1] 张湘平,张金槐,谢红卫.验前信息与现场子样的相容性检验方法研究[J].飞行器测控学报(Journal of Spacecraft TT and C Technology),2002,21(1):55-59.
[2] 唐雪梅.小样本场合下相容性检验方法[J].系统工程与电子技术(Systems Engineering and Electronics),2001,23(10):66-80.
[3] 王 晖,潘高田,臧兴震,等.正态分布的小样本数据的相容性检验理论和方法[J].数学的实践与认识(Mathematics in Practice and Theory),2005,35(3):131-137.
[4] 潘高田,潘 峰,王 晖,等.顺序统计量在小样本检验中的理论和方法研究[J].工程数学学报(Chinese Journal of Engineering Mathematics),2005,22(2):301-306.
[5] 李 姝.导弹系统仿真模型验证方法研究[D].长沙:国防科技大学,2003.
[6] 魏宗舒.概率论与数理统计教程[M].北京:高等教育出版社,1982.
[7] 张金槐,唐雪梅,邵凤昌.武器装备小子样试验分析与评估[M].北京:国防工业出版社,2001.
Static consistency inspection under small sample circumstance based on statistic of difference quotient ratio series in variable metric
HAO Jin-feng1,GUO Hui2,LI Jing-zhong1,WANG Qi3,XU Cheng4
(1.The Sixth Department,Ordnance Engineering College,Shijiazhuang Hebei 050003,China;2.College of Foreign Languages,Hebei University of Science and Technology,Shijiazhuang Hebei 050018,China;3.No.66440 Unit of PLA,Shijiazhuang Hebei 050081,China;4.No.78636 Unit of PLA,Shifang Sichuan 618419,China)
The paper presents some methods of static consistency inspection for simulation data under small sample circumstance with order statistics.Based on the discussion of these methods and by using some results for reference,the consistency inspection based on the statistic of difference quotient ratio series in variable metric is improved,which is fit for arbitrary distributions and has a better inspection effect.
small sample;consistency inspection;rank sum test;order statistics;statistic of difference quotient ratio series in variable metric
O635
A
1008-1542(2011)05-0413-04
2011-04-05;
2011-08-27;责任编辑:张 军
郝晋峰(1984-),男,河北新乐人,博士研究生,主要从事装备维修保障等方面的研究。
