图书借阅预测的ARIMA乘积季节模型构建及实证分析①

刘 琳

(华北科技学院图书馆，北京东燕郊 101601)

图书借阅预测的ARIMA乘积季节模型构建及实证分析①

刘 琳②

(华北科技学院图书馆，北京东燕郊 101601)

本文研究乘积季节模型在我校图书借阅预测中的应用，通过对我校2007年1月到2009年12月的月度图书借阅数据来进行实证分析，采用差分方法对序列资料进行平稳化，然后进行模型定阶并估计其参数，建立了我校图书借阅的乘积季节预测模型ARIMA(4，1，1)(1，1，1)12。对模型进行诊断检验，结果表明，用该乘积季节模型对我校的图书借阅拟合效果较好。最后，利用此模型对我校2010年1至6月进行了预测，与实践有较好的拟合。

乘积季节模型;时间序列分析;图书借阅量;预测

0 引言

图书馆作为高校的第二课堂，主要满足在校教师和学生的学习研究的资料查询及借阅需求。图书借阅预测和分析对图书资料的管理和用户行为的调节等都具有十分积极的意义。

目前国内对图书借阅预测比较活跃，但建模研究基本上是季节性AR模型。本文探讨了采用乘积季节型模型，对我校图书借阅的预测结果表明，该模型具有较好的拟合效果。

1 乘积季节模型

1.1 乘积季节模型简介

时间序列分析是一种根据动态数据揭示系统动态规律的统计方法，其基本思想是根据系统的有限长度的运行记录，建立能够比较精确地反映时间序列中所包含的动态依存关系的数学模型，并借此模型对未来行为进行预测。

ARIMA模型属于随机时间序列分析方法。随机序列分为平稳序列(统计特征不随时间变化)和非平稳序列(不具有平稳性)，对于平稳时间序列可以建立自回归模型(AR(p))、移动平均模型(MA(q))和自回归移动平均模型(ARMA(p，q))。非平稳的时间序列可以先进行d阶差分运算，然后建立 ARMA模型，即 ARIMA(p，d，q)模型。乘积季节模型是随机季节模型与ARIMA模型的结合。

包含季节性的时间序列也不能直接建立ARMA模型，须进行季节差分消除序列的季节性，差分步长与季节周期一致，一般地，如果序列经过D

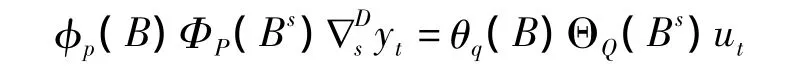
式中，p是季节自回归阶数，q是季节移动平均阶数，并且分别Φp(Bs)和ΘQ(Bs)季节P阶自回归算子和Q阶移动平均算子。

1.2 乘积季节模型的建模步骤

建立乘积季节模型可归纳为3个具体步骤:数据的平稳化;模型的识别、定阶与模型参数估计;模型的诊断检验。

1.2.1 数据的平稳化

一般对非平稳数据通过差分或取对数等方式可以将其平稳化。

1.2.2 模型的识别与定阶

对乘积季节模型的阶数识别及参数估计，基本上采用Box-Jenkins方法，也就是立足于考察数据的自相关和偏自相关分析图，季节长度s可以由实际应用背景分析得到。

1.2.3 诊断检验

模型是否合适，需要对其进行拟合优度检验，典型的方法是对残差序列进行分析，如果残差序列不是白噪声序列，则说明还有信息包含在相关的残差序列中未提取出来，必须修改模型，直到残差序列是白噪声序列为止。阶周期长度为s的差分，季节性基本消除，如果在季节差分之前还进行了d阶逐期差分才平稳，则可以对原序列建立乘积季节模型ARIMA(p，d，q)(P，D，Q)s，记为

2 实证分析

2.1 样本选取

本文选取的数据为华北科技学院图书馆2007年1月到2010年6月的图书借阅数据(数据来源于图书馆管理信息系统统计的结果)，我们处理的数据为2007年1月到2009年12月，2010年的数据作为预测数据。

将借阅量的原始数据绘成折线图，如图1所示，序列是具有明显的增长趋势的非平稳序列，并包含周期为12个月的季节波动。

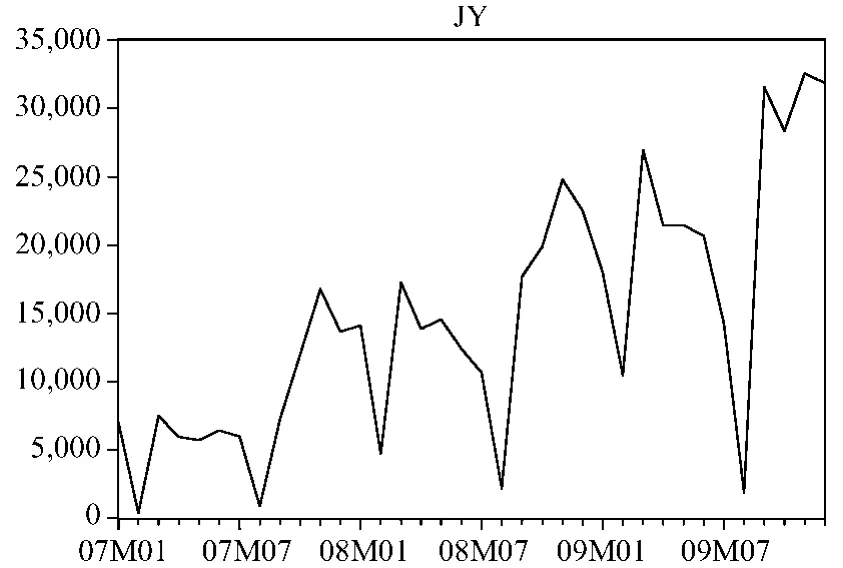
图1 图书借阅量折线图

2.2 数据处理

为消除趋势同时减少序列的波动，对原序列做一阶自然对数逐期差分，得新序列，记为sjyl，即sjyl=log(jyl)-log(jy(-1))。

根据序列sjyl的自相关和偏相关分析图可以看出序列趋势基本消除了，但k=12时，样本的自相关和偏相关系数显著不为0，表明季节性存在。对序列sjyl做季节差分，记为ssjyl，即

ssjyl的自相关和偏相关分析图如图2所示。

从序列ssjyl的自相关与偏相关分析图可见，序列趋势和季节性已基本消除，进一步检验序列均值为0的假设可接受。

为了进一步检验序列是否平稳，对进行单位根检验，单位根检验是平稳性检验的正式方法。

从表1可看出，p检验值小于给定的显著性水平，拒绝原假设，认为序列不存在单位根，是平稳的。表明对序列ssjyl可以直接建立ARMIA模型了。

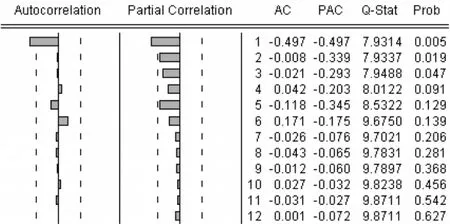
图2 序列ssjyl的自相关与偏相关分析图

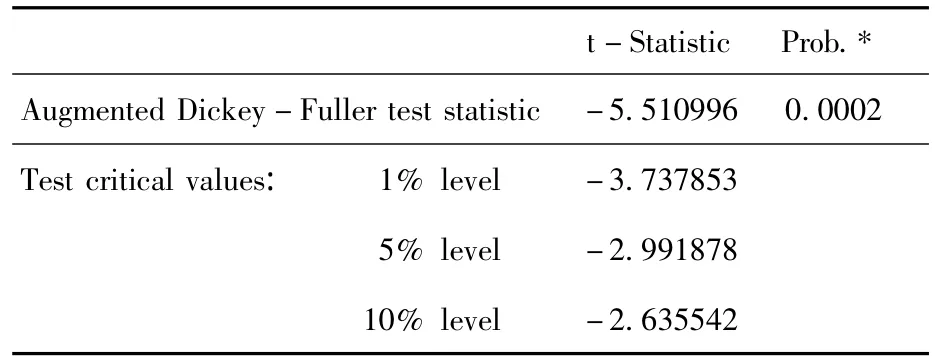
表1 ssjyl序列的单位根检验

2.3 模型识别

因为经过一阶逐期差分，序列趋势已基本消除，故d=1;经过一阶季节差分，季节性基本消除，故 D=1。所以选用 ARMIA(p，d，q)(P，D，Q)s模型。观察序列ssjyl的自相关与偏相关分析图，q=1，p=2或p=3比较合适，考虑到AR模型是线性方程估计，相对于MA和ARMA模型的非线性估计容易，且参数意义便于解释，故在实际建模中一般希望用高阶的AR模型替代相应的MA或ARMA。综合考虑，可以选择的(p，q)组合可以有:(3，1)，(4，0)，(4，1)。由于 k=12 时，样本的自相关与偏相关系数都显著不为0，所以，P=Q=1。

2.4 模型的建立

利用计量经济软件Eviews6.0，可以直接建立模型，求解参数系数，如建立 ARIMA(4，1，1)(1，1，1)12模型。在主菜单选择Quick/Estimate Equa-tion，打开方程定义对话框，输入

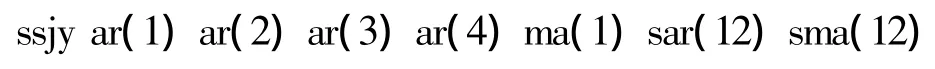
其中，sar(s)和sma(s)分别表示季节自回归部分和季节移动平均部分的变量。

点击确定后，得到图3所示的结果。

2.5 模型选择与检验

将三个模型的参数估计和相关检验结果汇总列入表1。

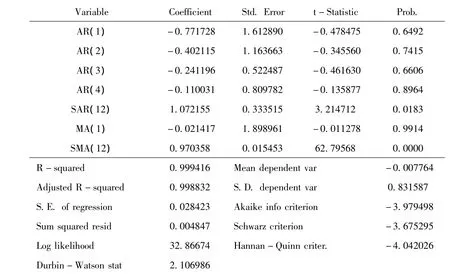
图3 模型参数估计与相关检验结果

表2 各模型参数估计结果及检验结果

经计算，各模型都满足ARMA过程的平稳条件及可逆条件，模型设定都合理，拟合效果较好，其中第3个模型的AIC值最小，因此最终选择第三个即 ARIMA(4，1，1)(1，1，1)12模型比较合适。

模型诊断通过残差序列检验来实现，如果残差序列是白噪声序列，则说明模型是适应的，否则模型需要改进。对以上乘积季节模型进行残差分析，残差序列单位根检验结果如表2，残差序列自相关和偏相关分析图结果如图4。

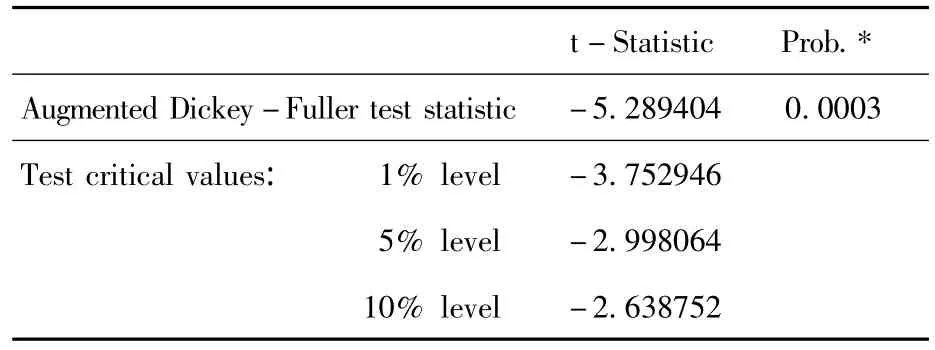
表3 残差序列的单位根检验

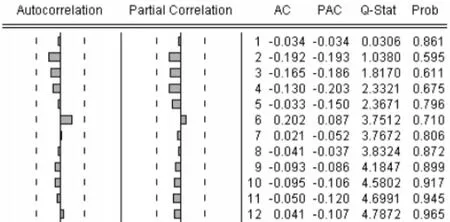
图4 残差序列的的自相关与偏相关分析图

残差分析表明，残差序列是平稳的白噪声，所建立的模型较好地拟合了时间序列的数据变化趋势。

2.6 预测

利用 ARIMA(4，1，1)(1，1，1)12模型，对我校2009年1月到2010年6月份的借阅量进行了预测，预测结果表3所示。

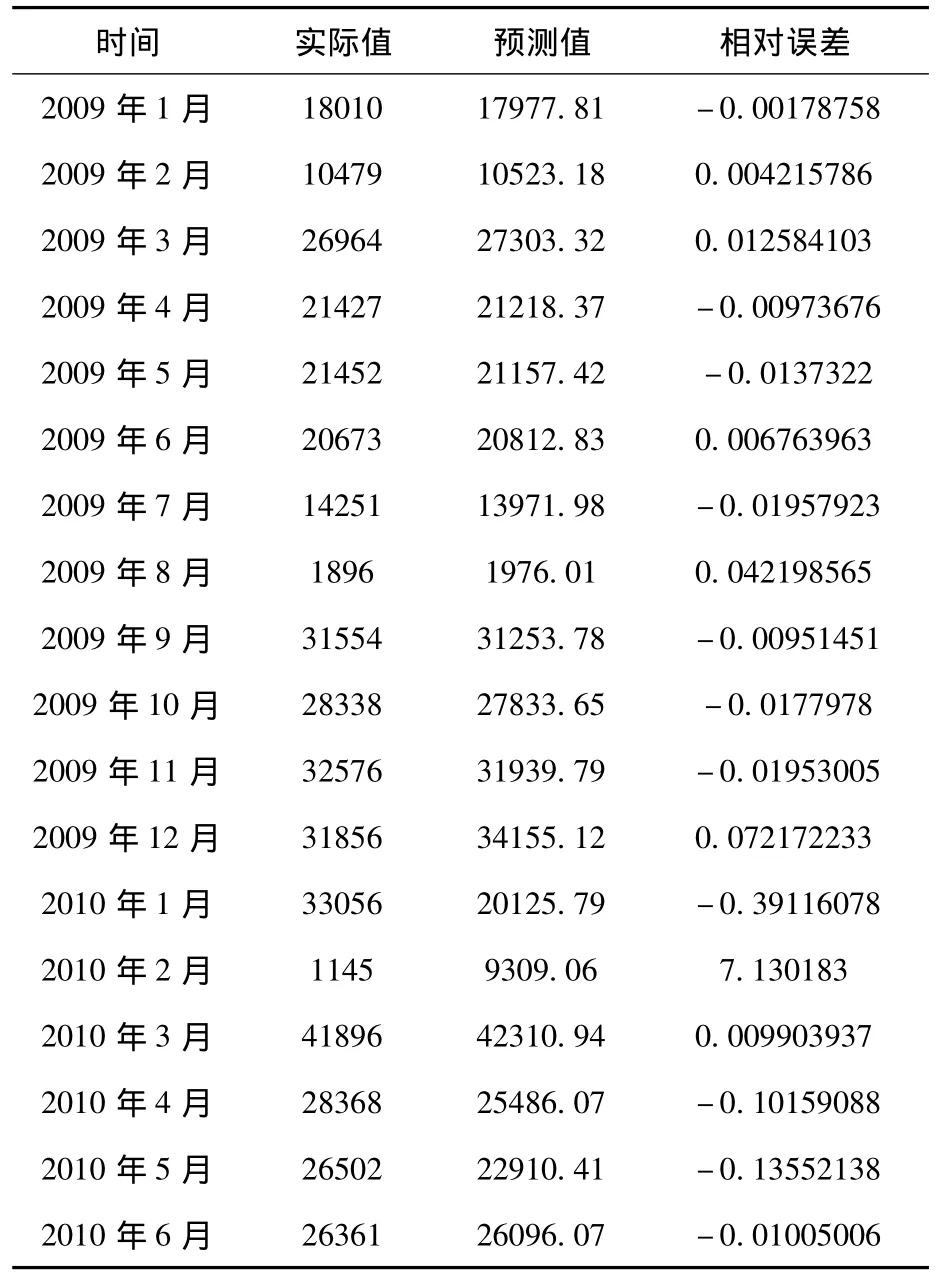
表4 实际值与预测值对比表

从预测结果可以看出，对2009的年数据预测效果非常精确，对2010年的数据除1月份2月份外，也比较精确，这2个月的数据出现大的偏差是因为2010年学校放寒假比往年提前了许多，开学又较晚，2月份学生基本上不在学校，从而导致了1月份的数据突然变大，2月份的数据突然很小，这是往年从来没有的现象，从而可以看做异常数据，不予理睬。除了这2个月异常外，其他4个月预测结果都非常的满意，精度很高，我们建立的乘积季节模型是比较理想的。从这里我们可以发现，利用此模型还可以发现异常数据，结合实际情况对异常情况作出合理解释。

3 结论

与一般时间序列模型相比，乘积季节模型需要更多的历史数据，相对于其他时序模型，乘积季节模型具有更广泛的适用范围，在现实的经济生活中具有明显的趋势和季节性特点的数据非常普遍，因此乘积季节模型较好地解决了这类问题的预测问题，精度较高。本文所建立ARIMA(4，1，1)(1，1，1)12模型较好地拟合了我校图书借阅规律，而且历史数据越丰富，模型预测的结果越精确，本文所介绍的乘积季节模型方法具有较好的实用性。

［1］ 易丹辉.数据分析与Eviews应用［M］.北京:中国人民大学出版社，2009

［2］ 彭志行等.ARIMA乘积模型及其在传染病发病预测中的应用［J］.数理统计与管理，2008，(3):75～79

［3］ 张欢.中国煤炭价格的ARIMA模型的建立及其预测分析［J］.广西师范大学学报(自然科学版)，2006，(2):9 ～13

Application of ARIMA multiplicative Seasonal Model to the Forecast for Books Borrowing

LIU Lin

(The library of North China Institute of Science and Technology，Yanjiao Beijing-East 101601)

This article mainly researched the application of multiplicative seasonal model to the forecast forHuake’s books borrowing.It empirically analyzed the number of books borrowing to our university from January 2007 to June 2010.applied difference method to stabilize the sequence data，then made order determination and parameter estimation for the model，established the multiplicative seasonal model ARIMA(4，1，1)(1，1，1)12.The diagnostic test showed that this model had good fitting results of forecasting the number of books borrowing，Finally，this model was applied to predict the books borrowing form January to June of 2010，and the result preferably fit the actual situation.

multiplicative seasonal model;time series;books borrowing;forecast

G250.7

A

1672-7169(2011)03-0105-04

2011-02-01

刘琳(1968-)，女，华北科技学院图书馆教师。