2n阶非线性差分方程周期解的存在性①

彭国荣 隋丽丽

(1.湖北民族学院预科教育学院，湖北 恩施 445000;2.华北科技学院基础部，北京 东燕郊 101601)

2n阶非线性差分方程周期解的存在性①

彭国荣1②隋丽丽2

(1.湖北民族学院预科教育学院，湖北 恩施 445000;2.华北科技学院基础部，北京 东燕郊 101601)

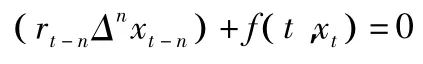
周期解;临界点;非线性差分方程多解性;变分方法

1 引言及主要结果

非线性泛函分析是现代数学的一个重要分支，它为解决当今科技领域中出现的各种非线性问题提供了富有成效的理论工具。在处理实际问题所对应的各种非线性方程中发挥着不可替代的作用。它的基本方法有拓扑度方法、锥与半序理论及变分方法等。

本文主要利用非线性泛函分析中的变分方法，结合临界点理论，研究2n阶非线性差分方程

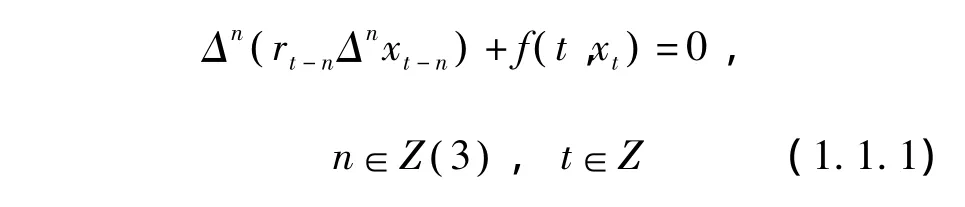
周期解的存在性与多重性。其中，Z( a)={ a，a+1，…}， 当 a ≤ b 时，Z (a，b)={a，a+1，…，b}，Δ 是向前差分算子，即 Δxt=xt+1-xt，Δk+1xt=Δ ( Δkxt)。实数序列rt和非线性项f分别满足以下条件:

(A)对给定的正整数 T，rt+T=rt＞0，t∈Z;

(B)f∈C( Z × R1→R1)，并且对任意 ( t，z)∈Z × R1，f( t+T，z)=f( t，z)。

我们的主要结论是:

定理1.1假设满足下列条件:

(2)存在 a＞0，c＞0，使得对任意(t，z)∈Z ×

(3)存在 ρ1＞0，使得当时，F( t，z)＞0

则问题(1.1.1)在ET中至少有两个非零解。

定理1.2假设下列条件满足:

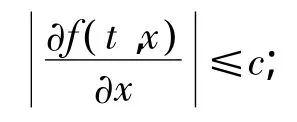
则问题(1.1.1)在ET中有三个不同的解。

2 变分结构

为了应用临界点理论，本节将定义问题(1.1.1)所对应的能量泛函，并讨论其相关性质。首先介绍一些概念和记号。

用S表示一切实数序列x= x{ }

nn∈Z所组成的集合，即

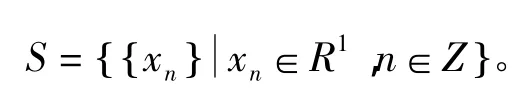
同时也用(…，x-n，x-n+1，…，x-1，x0，x1，x2，…，xn，…)表示 x={xn}n∈Z。对于给定的正整数T，集合ET定义为

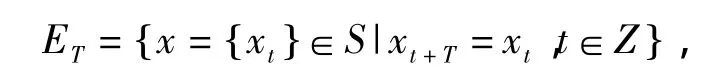
则ET为S的线性子空间，并且与RT同构。定义ET上的内积为

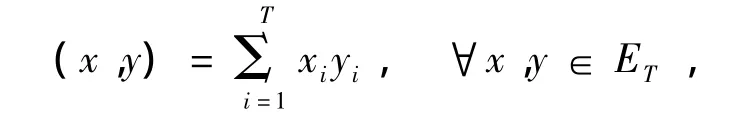
由此内积诱导出空间ET上的范数记为:

易证明问题(1.1.1)的周期解等价于J在ET上的临界点。

证明我们的结论需要如下引理。

引理2.1［1］设θ是J的一个临界点且J(θ)=0，并且J在θ点有一个关于E=V1⊕V2的局部环绕，其中 k=dimV1＜∞，即存在充分小的 ρ＞0使得

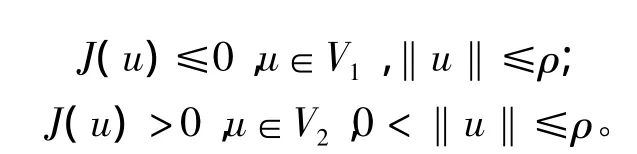
那么Ck(J，θ)≠0，即θ是J的一个同调非平凡临界点。

引理2.2［2］假设J满足P.S.条件且有下界，如果J有一个同调非平凡、非极小的临界点，则J至少有三个临界点。

引理2.3［3］设 H 是实的 Hilbert空间，f:H→R1是 C1泛函，F=gradf，ΩR={x∈H:‖x‖ ＜R}，Ωr={x∈H:‖x‖ ＜r}，其中 R ＞r＞0是两个实数。假定

(1)在H的任何有界集S上都满足Lipschitz条件，即存在常数KS＞0使得‖F(x)-F(y)‖≤KS‖x-y‖，∀x，y∈S;

(2){xn}有界，F(xn)→θ蕴涵{xn}有收敛子列;

(3)∀x∈∂Ωr，(F(x)，x)＞0;∀x∈∂ΩR，(F(x)，x)＜0，或者满足∀x∈∂Ωr，(F(x)，x)＜0;∀x∈∂ΩR，(F(x)，x)＞0。

那么泛函f在ΩR内有三个临界点。

3 主要结果的证明

为了证明主要结论我们需要如下引理

的最小非零特征值。

证明由矩阵知识知A是半正定矩阵，其特征值为 0 ＜λ1≤ λ2≤ …≤ λT-1。显然，ξ=( v，v，…，v)T∈ET是所对应的特征向量(v≠0，v∈R1)，并且 ξ∉Y。

下面用数学归纳法证明该不等式成立。

设 x=(x1，x2，…，xT)T∈Y，当 n=1 时，

下面我们将给出定理1.1和1.2的证明。

定理 1.1的证明由 F(t，z)的定义知 F(t，0)=0，从而 J(θ)=0。由假设条件(1)得 f(t，0)=0。从而J'(θ)=0。由引理3.1及假设条件(2)知J有下界，满足P.S.条件。

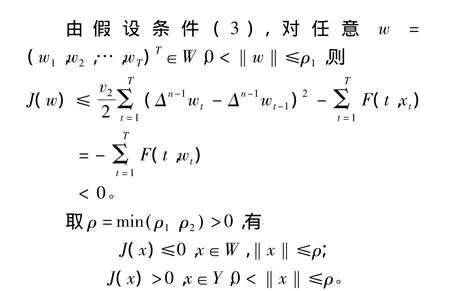
从而由引理2.1知θ是J的一个同调非平凡临界点，又因为θ是J的非极小值点，所以由引理2.2知J至少有三个临界点。即问题(1.1.1)在ET中至少有两个非零解。

定理1.2的证明我们证明泛函J(x)在ET中至少有三个不同的临界点。

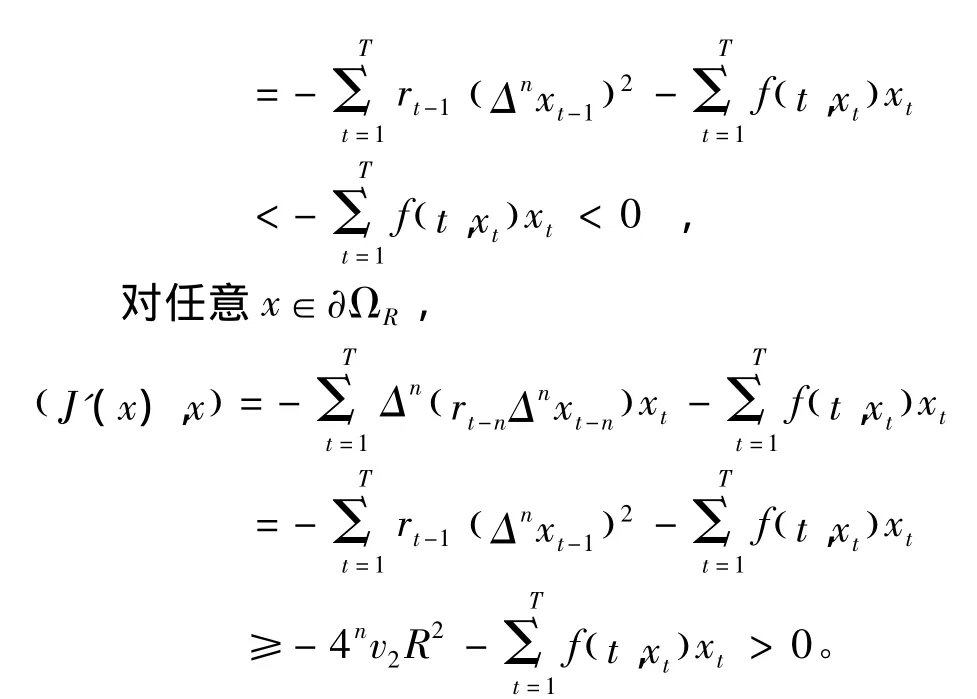
因此，泛函J满足引理2.3的所有假设条件，所以由引理2.3知泛函J在ET中至少有三个不同的临界点，即问题(1.1.1)在ET中至少有三个不同的解。

［1］ Benshi Zhu，Jianshe Yu.Multiple positive solutions for resonant difference equations［J］.Mathematics ＆ Computer Modelling，2009，(49):1928-1936

［2］ J.H.Zhang，S.J.Li，Multiple Nontrivial Solutions for some Fourth Order Semilinear Elliptic Problems［J］.Nonlinear Analysis，2005，(60):221-230

［3］ 郭大钧.非线性泛函分析(第二版)［M］.济南:山东科学技术出版社，2001

Existence of Periodic Solutions for A 2n Th-ordern Oolinear Difference Equation

PENG Guorong，SUI Lili

(1.Hubei institute for Nationalities Pre-Institute Department，Enshi Hubei445000;
2.Foundation department of North China Instituteof Science and Technology，Yanjiao Beijing-East 101601)

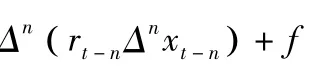
multiplicity of solutions;energy functional;variational method;critical point theory;critical group;Morse theory

O175.7

A

1672-7169(2011)03-0078-04

2011-01-12

彭国荣(1983-)，男，湖北民族学院预科教育学院教师。