广义正则长波方程的拟紧致守恒差分格式

胡劲松，王玉兰

（西华大学数学与计算机学院，四川 成都 610039）

广义正则长波方程的拟紧致守恒差分格式

胡劲松，王玉兰

（西华大学数学与计算机学院，四川 成都 610039）

对广义正则长波方程的初边值问题进行了数值研究，提出了两层隐式拟紧致差分格式，该格式很好地模拟了问题的守恒性质，得到了差分解的存在唯一性，并利用能量方法分析了该格式的二阶收敛性与无条件稳定性.数值结果表明，该格式的精度明显好于一般的二阶格式.

广义正则长波方程；差分格式；守恒；收敛性；稳定性

在对非线性扩散波的研究时，Peregrine在文献［1-2］中提出了正则长波（RLW）方程，由于它所描述的运动有与KDV方程相同的逼近，而且能很好地模拟KDV方程的几乎所有应用，因此备受关注.但是RLW方程少有解析解，所以讨论其数值解法就显得很有意义［3－7］.

其中σ和x0是任意常数.因此，只要选取－xL，xR足够大，则初边值问题（1）—（3）与方程（1）的Cauchy问题是一致的.文献［3］对问题（1）—（3）提出了具有二阶精度的三层守恒差分格式，但三层格式在计算时不是自启动的；文献［4］对问题（1）—（3）提出了具有二阶精度的两层守恒差分格式，但其对方程（1）中的非线性项（up）x的离散太过复杂，尤其是当参数p较大时，计算耗时很大.本文在保持理论精度不变的情况下，对非线性项（up）x提出了比文献［4］更简单的离散方法，再利用文献［7-8］中的处理思想，构造了问题（1）—（3）的一个两层拟紧致隐式差分格式，格式合理地模拟了守恒量（4），从而适合长时间计算.数值算例表明，相对于一般的二阶格式［4］，该格式的精度有了明显的提高.

1 差分格式的建立和守恒律

2 差分格式的可解性

3 差分格式的收敛性与稳定性及其解的唯一性

定理5在定理4的条件下，差分格式（6）—（8）的解un以‖·‖∞稳定.

定理6差分格式（6）—（8）的解是唯一的.

4 数值实验

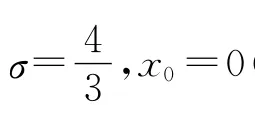
表1 格式1与格式2在不同时刻的l∞误差比较

从表1可以看出，本文的格式是可行的，且格式1的精度明显优于格式2.

［1］ PEREGRINE D H.Calculations of the development of an unduiar bore［J］.J Fluid Mech，1966，25：321-330.

［2］ PEREGRINE D H.Long waves on beach［J］.J Fluid Mech，1967，27：815-827.

［3］ ZHANG L.A finite difference scheme for generalized regularized long-wave equation［J］.Appl Math Comput，2005，168（2）：962-972.

［4］ 王廷春，张鲁明.求解广义正则长波方程的守恒差分格式［J］.应用数学学报，2006，29（6）：1091-1098.

［5］ RAMOS J I.Explicit finite difference methods for the EW and RLW equations［J］.Appl Math Comput，2006，179（2）：622-638.

［6］ BHARDWAJ D，SHANKAR R.A computational method for regularized long wave equation［J］.Comput Math Appl，2000，40：1397-1404.

［7］ 王廷春，张鲁明.正则长波方程的新型守恒差分算法［J］.高等学校计算数学学报，2005，27（6）：19-23.

［8］ 王廷春，张鲁明.对称正则长波方程的拟紧致守恒差分逼近［J］.数学物理学报，2006，26A（7）：1039-1046.

［9］ 柏琰，张鲁明.对称正则长波方程的一个守恒差分格式［J］.应用数学学报，2007，30（2）：248-255.

［10］ BROWDER F E.Existence and uniqueness theorems for solutions of nonlinear boundary value problems［J］.Proceedings of Symposia in Applied Mathematics，1965，17：24-49.

Pseudo-compact conservation difference scheme for generalized regularized long wave equation

HU Jin-song，WANG Yu-lan
（School of Mathematics and Computer Engineering，Xihua University，Chengdu 610039，China）

The numerical solution for an initial-boundary value problem of generalized regularized long wave equation is considered.An implicit pseudo-compact finite difference of two levels is proposed.This scheme simulates the conservation properties of the problem well.And the existence and uniqueness of the solution are obtained.It is proved that the finite difference scheme is convergent with order 2and stable without condition by the energy method.The numerical examples show that the accuracy of this scheme is better than usual difference scheme of two levels.

generalized regularized long wave equation；finite difference scheme；conservation；convergence；stability

O 241.82

110·61

A

1000-1832（2011）03-0039-05

2009-04-25

国家自然科学基金资助项目（40701014）；西华大学重点学科项目（XZD0910-09-1）.

胡劲松（1973—），男，硕士，副教授，主要从事计算数学研究.

陶 理）