红外灯阵热流分布仿真优化研究

杨国巍 苏新明 裴一飞 陈金明

(1 北京空间飞行器总体设计部,北京 100094)

(2 北京卫星环境工程研究所,北京 100094)

1 引言

红外灯阵作为一种空间外热流模拟装置,被广泛应用于航天器真空热试验中。红外灯阵由红外单灯组件、挡板、支架构成,如图1所示。红外灯阵利用了一组红外单灯的热辐射来实现对被辐照面的加热,针对被辐照面的面积、最高温度(热流)值和热流均匀性的要求,对红外灯阵的尺寸和红外单灯的布局进行设计。

使用红外灯阵加热时,热流不均匀性一般不超过±10%[1]。为了达到上述要求,试验开始前,需要对灯阵进行均匀性测试,即调整单灯在灯阵中的安装位置,使灯阵的热流不均匀性在(-10%～+10%)范围内。这一过程比较繁琐且耗费人力。为了有效缩短灯阵热流不均匀性测试时间,方便快捷地完成灯阵安装,有必要通过数值方法对红外灯阵热流分布进行优化分析计算,在灯阵进行热流不均匀性测试前期,获得合理的单灯安装位置。

图1 红外灯阵示意图Fig.1 Schematic diagram of infrared lamp array

目前国内外用于航天器外热流模拟的红外灯的种类及型号有所不同。美国NASA航天器真空热试验中通常采用Research 公司生产的红外灯[2]。德国LABG 公司采用型号为13195X/98,额定功率为1 000W 的飞利浦红外灯[3]。在我国航天器真空热试验中,也采用了飞利浦红外灯,型号为13169X/98。本文即以该种红外灯为研究对象,建立了我国航天器真空热试验使用的红外灯阵热流分布优化计算方法。该方法考虑了红外灯阵的实际安装情况,利用遗传算法对红外灯阵的热流分布进行寻优计算,以热流不均匀性不超过±10%为考核目标,得到最佳的单灯安装位置。本文计算的结果可以直接应用于红外灯阵热流不均匀性测试,使红外灯阵热流均匀性优化达到工程实践要求,减少试验调整时间,并为红外灯阵排布提供指导准则。

2 红外灯阵热流模拟

为了实现对红外灯阵热流的优化分析,需要解决红外灯阵热流的仿真计算问题。由于难以获得解析解,因此在既往研究和工程实践中,红外灯阵热流仿真计算主要采用蒙特卡洛方法[4-5]。但蒙特卡洛方法的缺点是计算速度较慢,根据以往经验,对于50个单灯规模的红外灯阵,若蒙特卡洛方法采用100万个粒子,则1次灯阵热流仿真就需要数小时时间。

红外灯阵热流仿真研究主要为优化研究做准备。在红外灯阵热流优化过程中,将多次频繁调用红外灯阵热流仿真模块。若热流仿真计算耗时较长,则后续优化计算的总时间将令人无法接受。因此必须寻找一种能够对红外灯阵的热流分布进行合理、快速、准确仿真的计算方法,供后续红外灯阵热流优化分析调用。

针对上述要求,本研究对于红外灯阵热流仿真的主要思路是:

1)基于蒙特卡洛方法获得红外单灯的热流辐射分布(无挡板)[5];

2)将不同网格点坐标的红外单灯热流分布数据集成为红外单灯热流分布数据库,网格点之间的红外灯热流视为线性分布;

3)在给定红外单灯坐标、旋转角度及被照面目标点坐标条件下,根据红外单灯热流分布数据库进行线性插值,得到红外单灯对目标点的直射热流;

4)在给定红外单灯坐标、被照面目标点坐标及灯阵挡板坐标的条件下,按镜面反射计算红外单灯通过挡板对目标点的反射热流;

5)对红外灯阵的所有红外单灯以及被照面的所有目标点,重复3)、4)计算,得到红外灯阵热流分布。

2.1 红外单灯热流分布

本文以矩形被照面为研究对象,单灯旋转角为0°。由于典型红外单灯水平方向有效热流辐射半径一般不超过1 000mm,垂直方向有效热流辐射半径一般不超过700mm,在此范围外的红外灯的辐照热流可以忽略。在红外单灯热流分布的蒙特卡洛法计算中,参数设置如下:

1)被照面为2 000mm ×2 000mm 的矩形平面;

2)被照面几何中心点为坐标原点,红外单灯轴线方向为X 轴,径向方向为Y 轴,高度方向为Z 轴,如图2所示;

3)红外单灯采用质点热源表示,设置于坐标原点正上方,高度可变,最大不超过700mm;

4)红外单灯参数(尺寸、阻值等)选取飞利浦13195X/98 型红外灯的相关参数;

5)被照面计算网格划分为100×100。

根据上述计算条件,分别采用蒙特卡洛方法计算不同高度(50mm～700mm,50mm 间隔)条件下,矩形平面被照面的红外单灯热流分布。在典型试验条件(高度300mm)下,红外单灯热流分布计算结果如图3所示。

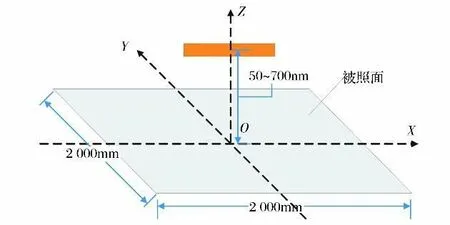
图2 红外单灯热流分布的蒙特卡洛计算(示意图)Fig.2 Monte Carlo calculation of heat flux distribution of single infrared lam p array(schematic diagram)

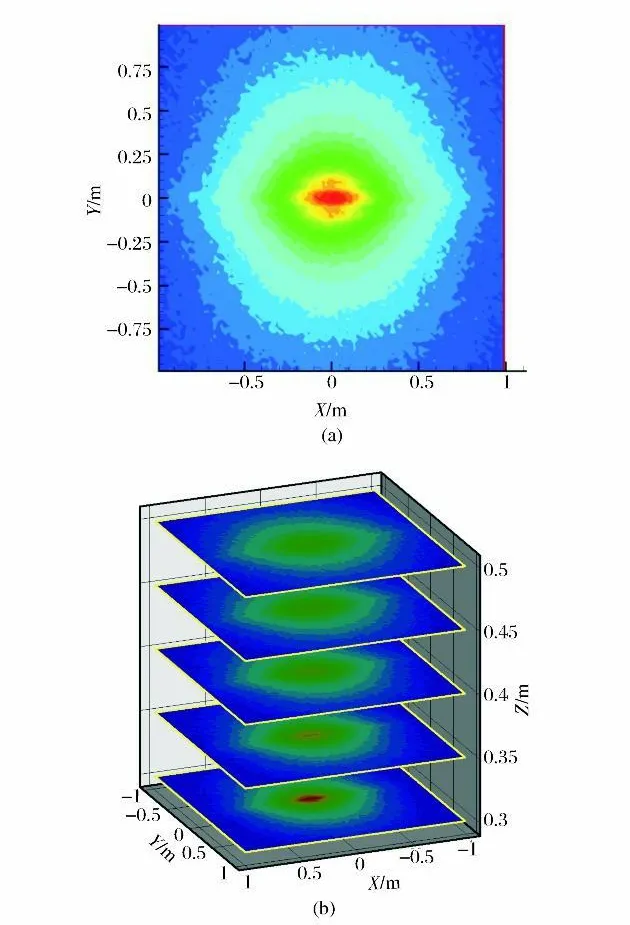
图3 红外单灯热流分布(蒙特卡洛法计算结果,旋转角为0°)Fig.3 H eat flux dist ribution of an infrared lamp array(Monte Carlo calculation,0°rotation angle)

汇总各种高度条件下的红外单灯热流计算结果,即可生成红外单灯热流分布数据库。红外单灯热流分布数据库是下一步红外灯阵热流分布仿真基础数据,采用二维数据表的形式描述红外单灯标准几何位置条件下的矩形平面被照面目标点热流分布。

2.2 红外单灯直射热流

如果红外单灯热流分布数据库的计算网格足够多,则网格间的红外灯热流可视为线性分布。因此对于任意位置红外单灯对于任意位置被照面目标点的直射热流辐射,可通过坐标变换将目标点坐标和红外灯原坐标转换为与红外单灯热流数据库相同的坐标系,然后将获得的红外单灯热流分布数据进行线性插值。

如图4所示,(Xsource,Ysource,Zsource)为红外单灯光源位置坐标,(Xdes,Ydes,Zdes)为被照面目标点坐标,X m、X m+1为热流数据库的X 向网格点,Y n、Y n+1为Y 向网格,Zk、Zk+1为Z 向网格。红外灯旋转角度为0,被照面为矩形平面。为了获得任意位置(Xsource,Ysource,Zsource)单灯在被照面任意位置(Xdes,Ydes,Zdes)处的直射热流,首先进行坐标变换,将绝对坐标转化为相对坐标:

因不考虑单灯旋转情况,因此可以直接根据ΔX、ΔY、ΔZ 以及红外单热流分布数据库,得出图3中Zk、Zk+1高度对于被照面标准坐标点的辐射热流值:Q(Zk,Xm,Yn),Q(Zk,Xm+1,Yn),Q(Zk,Xm,

图4 红外单灯相对被照面目标点的辐照热流插值计算示意Fig.4 Radiation heat flux interpolation calculation of infrared lamp array relative to aim point

根据以上网格点的热流值进行线性插值,即可得到(Xsource,Ysource,Zsource)处红外灯对(Xdes,Ydes,Zdes)处目标点的直射热流值Q(ΔZ ,ΔX ,ΔY):

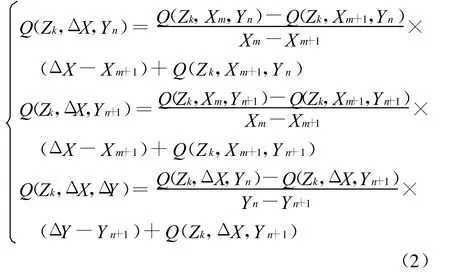
按照类似的过程,可以求得Q(Zk+1,ΔX ,ΔY),于是得出:

2.3 挡板反射热流

根据红外灯阵实际安装结构,在灯阵四周都有反光挡板,因此存在反射热流,对热流不均匀性同样有影响,尤其是在被照面边缘部位影响更加明显。为了简化分析挡板反射热流的影响,做如下假设:

1)红外灯对被照面目标点的反射热流,由通过所有灯阵挡板反射热流的线性叠加构成;

2)通过灯阵挡板的热流反射按镜面反射考虑;

3)红外灯通过灯阵挡板的反射热流,视为红外灯对“被照面目标点相对于挡板的对称镜像点”直射热流的镜面反射;

4)每经过一次挡板反射后热流均有所衰减,因此不考虑三次以上的挡板反射热流。

对于一次反射热流,如图5所示,图中虚线部分为灯阵挡板,(Xsource,Ysource,Zsource)为红外单灯光源,(Xdes,Ydes,Zdes)为被照面目标点。MU(Xdes,Ymirror,Zdes)为目标点相对于上方挡板镜像点,ML(Xmirror,Ydes,Zdes)为目标点相对于左方挡板镜像点,镜像坐标可根据目标点坐标和挡板坐标求得。Q0为直射热流。QL、QR、QU、QD为通过四个挡板的反射热流,可视为红外灯光源对各挡板镜像点的直射热流经过一次挡板反射的结果,即

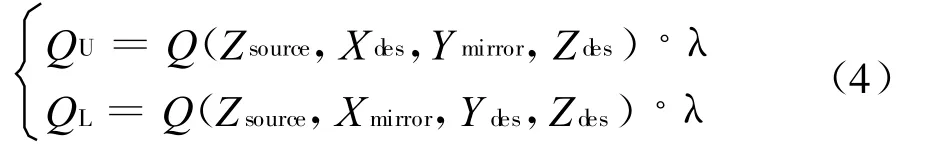
式中Q(Zsource,Xdes,Ymirror,Zdes)为位于Zsource高度的红外灯对于上挡板镜像的直射热流,Q(Zsource,Xmirror,Ydes,Zdes)为红外灯相对于左挡板镜像的直射热流,λ为挡板镜面反射率。同理可求得QR和QD。

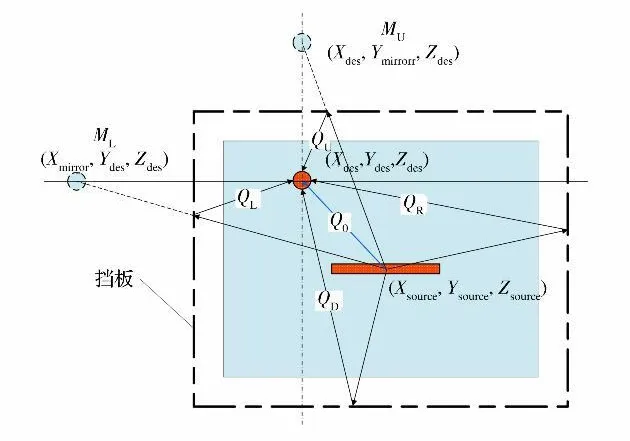
图5 通过挡板的一次反射热流计算(示意图)Fig.5 Heat flux of the first reflection through baffle(schematic diagram)

图6 通过挡板的二次反射热流计算(示意图)Fig.6 H eat flux of the second reflection through baffle(schematic diagram)

对于二次反射热流,如图6所示,图中MU为上挡板镜像,ML为左挡板镜像,MLU为左、上挡板的二次镜像,QLU为通过左、上挡板的二次反射热流,其它符号意义同图5。

与一次反射热流计算类似,QLU可视为红外灯光源对左、上挡板二次反射镜像点直射热流经过两次挡板反射的结果,即

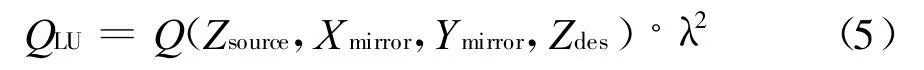
同理,可求得通过其它挡板的二次反射热流QLD(左、下挡板)、QLU(右、上挡板)、QRD(右、下挡板)。

2.4 挡板间隙漏光量

由于灯阵挡板下缘不会与被照面直接接触,存在一定的间隙EZ,,如图7所示,因此存在着从间隙漏光的问题。

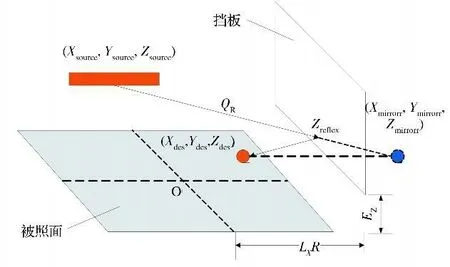
图7 红外灯阵挡板高度方向间隙对反射热流的影响Fig.7 Influence of baffle gap in height on reflection heat flux

根据光线的传播特性,以及被照点的镜面点位置,可以确定反射点的高度方向坐标Zreflex。若Zreflex＜EZ,则光线从间隙漏出,挡板反射热流为0。对于二次反射热流是否漏光,可采取类似的方法判断。

综上所述,红外单灯对于被照面目标点总热流Q为直射热流与反射热流之和,即:

上式中的一次反射热流和二次反射热流是已经考虑了漏光情况的修正值。

2.5 热流仿真模型验证

为检验本研究关于红外灯热流仿真计算的准确性,同时采用蒙特卡洛方法和本研究模型分别对相同试验条件下的红外灯阵热流分布进行了仿真计算。计算参数如下:

1)红外灯阵尺寸2 500mm ×2 300mm(实际被照面2 350mm ×2 150mm),EX、EY为挡板距离被照面的水平间隔;

2)EX=75mm,EY=75mm,EZ=50mm;

3)挡板镜面反射率为0.5;

4)红外单灯数量48 支,6 列8 行均匀分布,高度为350mm;

5)所有红外灯旋转角均为0°。

图8示出了蒙特卡洛方法计算结果(热流均匀性T =19.3%),图9示出了本研究模型仿真结果(热流不均匀性T =17.8%)。结果表明,本研究提出的插值算法热流分布仿真结果符合实际物理规律,与蒙特卡洛算法结果相近,热流不均匀性相对误差小于2%。

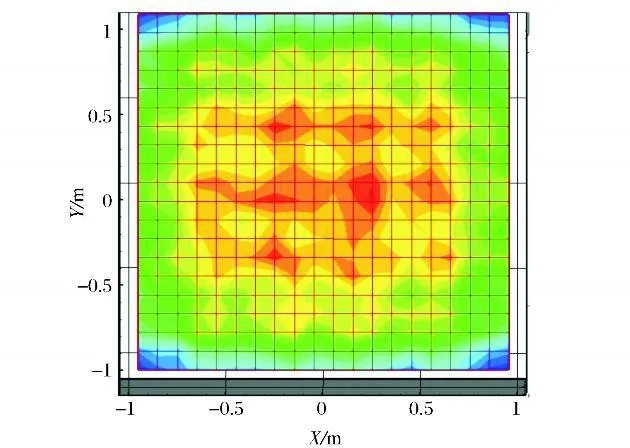
图8 红外灯阵热流分布模型验证,蒙特卡洛算法T =19.3%Fig.8 Validation of heat flux model of infrared lamp array,Monte Carlo calculation T =19.3%

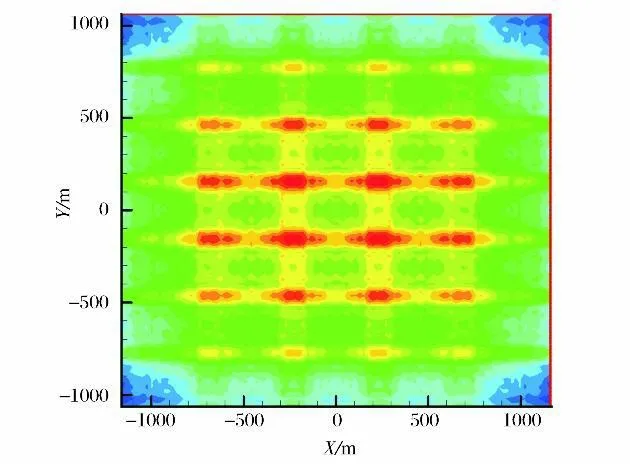
图9 红外灯阵热流分布模型验证,本研究模型T =17.8%Fig.9 Validation of heat flux model of infrared lamp array,the model of this paper T =17.8%

由此可见,采用红外灯阵热流仿真方法得到的计算结果与采用蒙特卡洛法计算得到的结果吻合良好,但本文计算过程仅用时5s,说明本文的计算方法可以用于复杂的红外灯阵热流分布优化计算。

3 红外灯阵热流分布优化计算

影响红外灯阵热流均匀性分布,主要有三类参数:

1)红外灯阵单灯相关参数,红外灯坐标、旋转角、单灯尺寸和阻值参数等;

2)红外灯阵挡板相关参数,挡板坐标、挡板垂直间隙和挡板反射率等;

3)被照面相关参数,包括被照面型式和被照面网格点划分等。

根据实际工程实践,在做优化计算之前对上述影响参数作如下约定:

1)红外灯无旋转角,单灯尺寸及阻值固定,为已知量;

2)红外灯阵挡板相关参数固定且为已知,计算中取挡板反射率为0.6;

3)被照面选取矩形平面,被照面网格划分可根据矩形尺寸进行调整。

由此可以确定红外灯阵热流分布不均匀性的优化目标为:在给定红外灯阵挡板参数和被照面参数的条件下,采用合适的优化算法,对红外单灯空间坐标进行优化分析,找出红外灯阵热流不均匀性满足要求时的各红外单灯的空间位置。

红外灯阵热流分布不均匀性优化问题的数学模型如下:

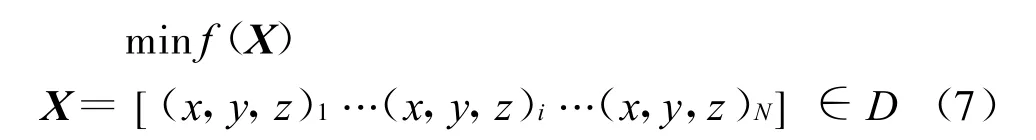
式中X为红外灯阵空间坐标组合向量;(x,y ,z)i为第i个红外单灯的三维空间坐标;N为红外灯数量;D表示红外灯坐标空间排布取值范围;f(X)为描述红外灯阵热流分布不均匀性的目标函数,一般采用相对误差均匀性和标准差均匀性两种,即

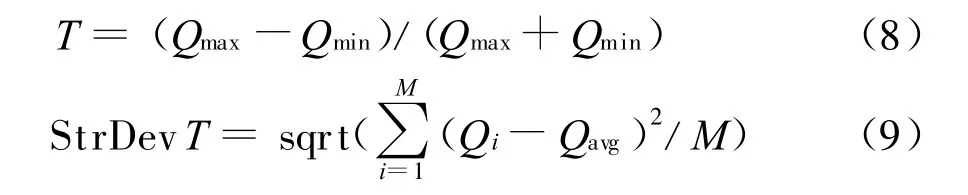
式中Qmax为被照面最大热流,Qmin为被照面最小热流,Qavg为被照面热流算术平均值,M为被照面网格点数量。

为了得出单灯最佳安装空间坐标,需采用合适的优化算法。遗传算法(Genetic Algorithm,GA)是一种自适应智能生物进化优化算法,具有天然的并行优化和全局优化特性,可同时跟踪优化多个参数,对目标函数梯度特性、连续性和单调性均无特殊要求,具有很强的鲁棒性,非常适合工程实践需求,因此可以将遗传算法用于红外灯阵热流不均匀性优化分析。

3.1 遗传算法[6]

遗传算法本质上是一种随机性优化方法,其优化过程首先是对所求问题进行编码,然后初始化一个种群,接着对整个种群反复进行选择、交叉、变异等遗传操作,从而使整个种群不断朝最优值方向迈进,直到得到满足工程要求的优化解。遗传算法虽然不能确定得到优化问题最优解,但随着遗传代数的增加,遗传算法得到的次优解会以概率1 趋近于最优解。遗传算法的流程图见图10。

遗传算法需设定的主要计算参数有:

1)群体规模(Size),表示每一代群体所包含的染色体数量。群体规模的取值主要取决于待优化参数的数量,一般在100～200 之间;

2)交叉概率(Pc),表示染色体发生交叉的概率。交叉算子是产生新个体的主要算子,Pc 的取值范围因具体问题不同可为0.5～0.95。本文取Pc为0.85;

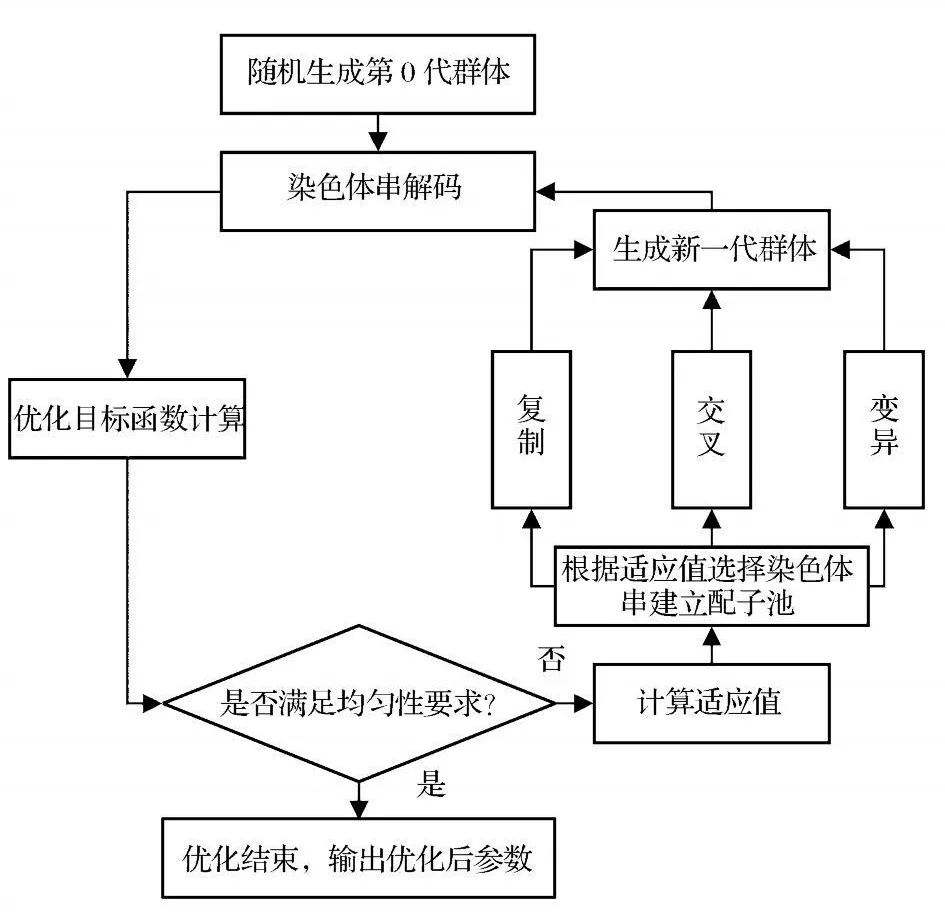
图10 遗传算法流程图Fig.10 Flow chart of Genetic Algorithm

3)变异概率(Pm),表示染色体发生变异的概率。Pm取值范围一般为0.01～0.1,本文取Pm为0.05;

4)终止代数(Age),表示遗传运算的代数。遗传算法是一种随机性优化算法,理论上可以无限制地进行计算趋近于最优解。因此设定一个终止代数,强制性地以终止代数的最优解作为优化结果。本文取Age为200;

5)优化目标值T0,即红外灯阵热流均匀性目标。红外灯阵热流均匀性可以用相对误差或标准差误差表征。本文按热流分布不均匀性相对误差设定优化目标值为T0为8%。

以红外灯安装坐标为待优化参数,结合工程实际经验,为了节省计算时间,将待优化参数进行合并调整以下两点:

1)对于平面矩形被照面,以中心为原点的对称轴对称,红外灯阵也与对称轴对称,所以可以只调节一个象限的红外灯阵排布,其他象限跟其对应即可。这样可以有效将待优化参数减少为原来的1/4;

2)红外灯在灯阵中的位置不是任意的,受到挡板的限制,以及安装的需要,一般要几只灯共同安装在一个支架上,如图1所示,因此在优化计算时可以将安装在同一个支架上的红外单灯X 坐标锁定(此时假设支架方向为Y 向),即几只红外灯的X 坐标相同,随支架移动共同变化。此时待优化参数进一步减少,如一支架上4只灯,则要计算的X 坐标由原来的4个缩减为1个。

3.2 优化计算

根据以上分析,对某平面矩形被照面的热试验使用的红外灯阵进行坐标优化计算。计算的优化条件如下:

1)平面矩形被照面,被照面尺寸3 680mm ×2 400mm;

2)挡板与被照面水平间距60mm ,垂直间距60mm,挡板反射率为0.6;

3)90 支红外单灯,按10 列9 行排布,旋转角度为0°,如图11所示。

4)计算中将灯阵进行列锁定,即安装在同一支架上的9只单灯,其X 坐标变化相同。

计算结束后,得到优化后的红外灯热流分布如图12所示,此时热流均匀性为5.99%,满足优化要求。灯阵优化后的安装坐标图如图13所示。

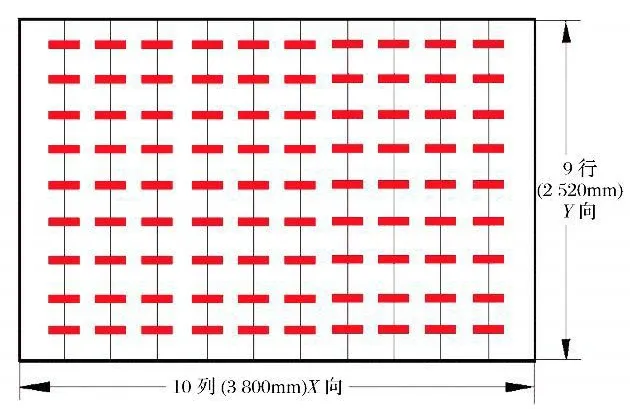
图11 计算用红外灯阵示意图Fig.11 Schematic diagram of infrared lamp array for calculation

可以看出,在灯阵四个角的位置上,单灯的安装高度较低,这是由于两块互相垂直的挡板对红外灯热流分布有很大影响,在该位置处的热流强度较低,为了在被照面上获得较均匀的热流,因此单灯的安装位置更接近于被照面,以获得足够强度的热流。

3.3 测试验证

图12 优化后的灯阵热流分布,T=5.99%Fig.12 Heat flux after optimization,T=5.99%

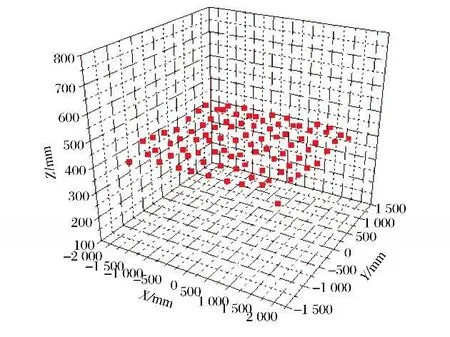
图13 优化后的灯阵安装坐标Fig.13 Installation coordinates of infrared lamp array af ter optimization

为了验证优化计算结果的正确性,根据3.2 节中优化计算得出的红外灯阵安装坐标,对某型真空热试验使用的红外灯阵进行均匀性测试。

使用热流均匀性测试系统对红外灯阵进行热流均匀性测试,如图14所示。测试仪通过在导轨上滑动以测遍被照面高度上所有位置的热流值。然后根据式(8)计算相对误差均匀性,与计算结果进行比较。

得到红外灯阵在被照面高度上的热流分布如图15所示,热流不均匀性为7.18%,满足热流不均匀性小于8%的要求。与优化计算结果相比,两者仅有1.19%的差异,说明热流分布优化计算是正确的。

4 结论

图14 均匀性测试Fig.14 Heat uniformity test

图15 实际测得灯阵热流分布,T=7.18%Fig.15 Aetual heat flux of aetual lamp array,T=7.18%

利用蒙特卡洛法进行了红外单灯热流分布计算,并据此建立了数据库,综合考虑红外灯直射热流、挡板反射率以及间隙漏光量等影响因素,得到红外灯阵热流分布。计算表明,本文的仿真结果与采用蒙特卡洛法计算得到的红外灯阵热流分布结果接近,证明本文进行热流仿真所采取的计算方法是正确的。此方法大大缩短了热流仿真所用时间,为进行红外灯阵热流分布优化提供了有力的保障。

通过结合工程实践,对实际红外灯阵进行了合理分析,最终将红外灯阵空间坐标作为待优化参数。其中在同一支架上的红外灯X 坐标锁定,共同变化。在优化过程中,利用遗传算法,以热流不均匀性小于8%作为优化目标,进行优化计算。对某型真空热试验使用的红外灯阵进行了优化计算,计算得到的热流不均匀性为5.99%,满足要求。根据计算得到的灯阵安装坐标对实际灯阵进行安装,并测试热流均匀性,测量得到的热流不均匀性为7.18%,同样满足要求,且与计算结果只有1.19%的差异,说明本文的计算结果是正确的,而且通过本文的计算过程,可以有效地缩短红外灯阵安装调试时间,避免了为获得合理的红外灯热流分布而采取的人工操作。通过优化计算得到的红外灯安装坐标可以直接应用于实际红外灯阵的安装,热流不均匀性的测试结果满足要求。

References)

[1]黄本诚,马有礼.航天器空间环境试验技术[M].北京:国防工业出版社,2002

[2]Ziemke R A.Infrared heater used in qualification testing of international space station radiators[R].NASA,TM-2004-212332,2004

[3]Frey H U.Design of test set-ups and thermal analysisfor space simulation tests with extreme temperature requirements[R].SAE Technical Paper,1995

[4]徐钟齐.蒙特卡洛方法[M].上海:上海科学技术出版社,1985

[5]尹晓芳,刘守文,郄殿福.红外灯热流分布试验研究[J].航天器环境工程,2010,27(1)

[6]王小平,曹立明.遗传算法—理论、应用与软件实现[M].西安:西安交通大学出版社,2002