航天器横向振动试验的力限条件设计研究

李正举 马兴瑞 韩增尧

(1 中国空间技术研究院,北京 100094)

(2 中国航天科技集团公司,北京 100048)

(3 北京空间飞行器总体设计部,北京 100094)

1 引言

航天器在发射和动力飞行期间要经受振动、冲击和噪声等动力学载荷,为了保证航天器及其各分系统和部组件能够经受住这些恶劣的动力学环境,必须进行充分的动力学环境试验。在传统的加速度控制振动试验中,试验夹具的机械阻抗与真实飞行构型中安装结构的机械阻抗存在很大的差异,如果仅采用加速度条件作为控制条件,可能导致严重的过试验现象[1]。力限振动试验则是在传统振动试验加速度控制的基础上引入力限条件,监测并限制试验夹具与试验件之间的界面力,使振动试验中界面处的响应更能接近真实的动力学环境,从而起到缓解振动“过试验”现象的目的[2-3]。

20 世纪90年代初,美国国家航空航天局(NASA)的喷气推进实验室(JPL)最早将力限振动试验技术应用于航天器振动试验中,并证明力限振动试验方法能够很好地缓解振动过试验问题[2-5]。国内在力限控制技术研究和应用方面尚处于起步阶段,航天器设计部门和试验部门也已认识到力限振动试验技术的重要性和迫切性[6-13]。

目前,在航天器的系统级和部组件级的力学振动试验中,采用的是依次进行三个方向(一个纵向、两个横向)的振动试验来模拟航天器在发射和飞行状态下实际动力学环境的试验方法,所以分别需要设计三个方向的力限条件,来限制振动台与试验件界面力谱密度,达到缓解过试验的目的。

在横向振动试验中,由于试验件质心位置与振动台横向激振力平面相距较远,试验件受到振动台三个方向力和三个方向力矩的作用,界面力分布情况比纵向振动试验复杂,试验件受到的纵向力、横向力和界面力矩都较大,此时界面力矩可以作为力限振动试验的一个重要的监测和控制参量[9]。所以有必要深入研究横向振动试验时力矩限制条件设计方法,实现力矩限控制横向振动试验,完善力限振动试验控制方式。

本文介绍了力限振动试验的基本原理;介绍了简单二自由度方法和复杂二自由度方法,基于二自由度系统模型推导了半经验系数的计算方法;然后基于模态有效质量概念提出了力矩限条件设计策略;最后计算了某航天器有效载荷的力限条件和力矩限条件,结果显示力矩限条件设计方法是可行和有效的,可以为今后我国力限振动试验提供技术支持。

2 模型构建

模态有效质量与结构的固有频率、振型和广义质量等模态特征量相关,反映结构系统刚体模态和弹性模态耦合作用的量,是评价结构基部受到动力学激励时模态重要性的标准之一。

通过正则模态分析,可以得到结构的模态有效质量Meff和刚体质量矩阵M,结构第k 阶模态有效质量为:

式中,Lk为模态参与系数,mk为第k 阶模态质量,Meff,k为6×6 阶模态有效质量矩阵。结构的刚体质量矩阵M 也为6×6 阶的矩阵,并且所有模态有效质量之和等于刚体质量矩阵。

在振动试验中,界面处的力FB与加速度x··B 之间的关系满足下式:

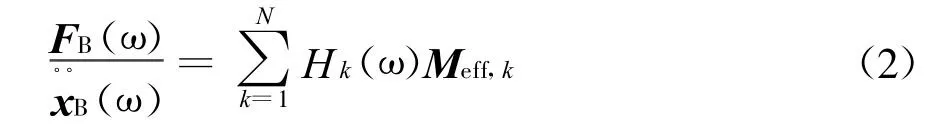
式中,Hk(ω)为模态频响函数,

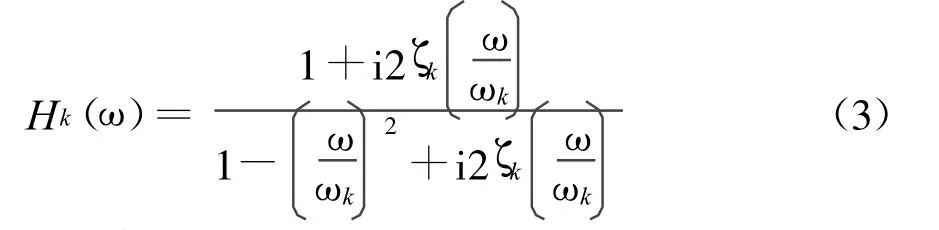
残余质量Mres为固有频率高于激励频率的模态有效质量之和,即

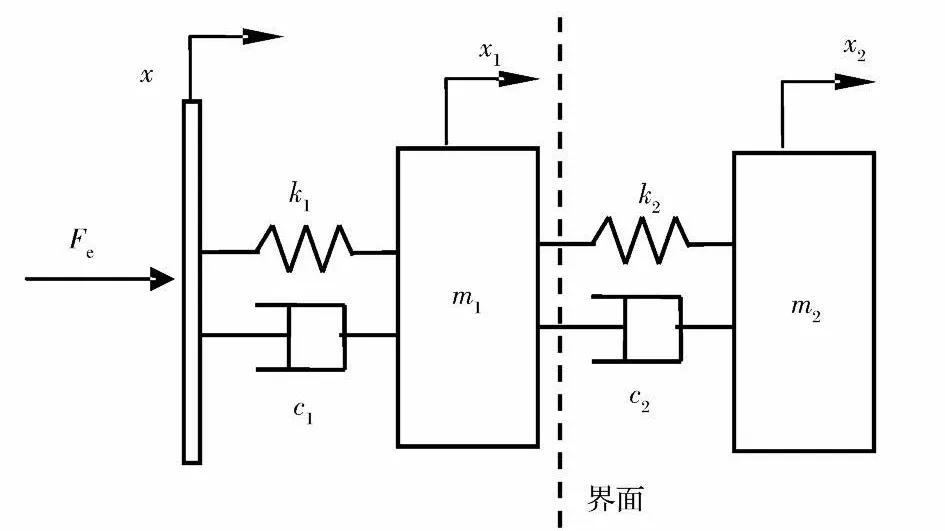
图1 简单二自由度模型Fig.1 Sim ple Two-Degree-of-Freedom-System

模态有效质量是构建力限条件设计简化模型的基础,首先在界面处分别计算负载和源的模态有效质量,并在每一个1/3倍频程频段内,依据式(4)和式(5)给出源和负载的等效模态质量和残余质量,然后将其组建为力限条件设计简化模型,如图1和图2所示。图1和图2中,m1和m2分别为源和负载的等效模态质量,M1和M2分别为源和负载的残余质量,k1和k2分别为源和负载的模态刚度,c1和c2分别为源和负载的模态阻尼,Fe为源所受的外力激励。在工程实践中也可通过振动台试验测得试验件的视在质量,并依据视在质量构建简化模型。

图2 复杂二自由度模型Fig.2 Complex Tw o-Degree-of-Freedom-System

3 横向振动试验的力矩限条件设计

横向振动试验中,试验件在振动台界面处受到的纵向力、横向力和界面力矩都较大,所以除了计算横向力限外,还应设计界面处力矩限,以完善力限振动试验的控制方式。

模态有效质量Μeff,k为6×6 阶模态有效质量矩阵,矩阵元素为mln,n为代表激励方向的分量号,l为代表界面力或力矩的分量号。在计算力限条件时,简化模型通常是由模态有效质量矩阵中的对角线元素ml l 构建而成。然而在横向振动试验力矩限条件设计时,应首先提取出模态有效质量中所需的非对角线元素mln(l ≠n),n为代表激励方向的分量号,l为所求界面力矩方向的分量号,由式(4)和式(5)构建简化计算模型,并依据简单二自由度方法、复杂二自由度方法和半经验方法[2-3,6]计算横向振动试验的力矩限条件,具体实施策略为:

1)对源和负载进行正则模态分析,得到模态参与系数Lk;

2)利用式(1)计算可以得到源和负载结构第k阶模态有效质量Μeff,k;

3)从模态有效质量矩阵中提取元素mln,n为代表激励方向的分量号,l为所求界面力矩方向的分量号;

4)构建简化模型,依据简单二自由度方法、复杂二自由度方法和半经验方法计算界面力矩限;

5)包络步骤4)得到的力矩限,得到可用于振动试验的力矩限条件。

4 算例

考虑某航天器上安装的相机结构,此航天器的有限元模型共有8 866个节点,10 132个单元随机振动试验中有效载荷相机的加速度条件见表1。

源的质量为592.5kg ,负载的质量为126.0kg。本文以Y 方向为例计算横向振动试验力限条件和力矩限条件设计。

表1 随机振动试验加速度条件Table1 Acceleration PSD for random vibration

此有效载荷随机振动试验的激励频率为20Hz～2 000Hz,计算力限条件时将其按1/3倍频程分为21个频段。分别用上面介绍的力限条件设计方法,在每一个频段计算出相应的力限和力矩限,然后进行包络,最后得到用于力限振动试验的力限条件和力矩限条件。

图3 Y 方向力限条件Fig.3 Force limit in Y direction

图3为Y 方向振动试验力限计算结果。在中心频率为200Hz 的频段复杂二自由度方法得到的力限最大,为6.50 ×105N2/Hz。力限条件:在80Hz～200Hz频段上力限为7.00×105N2/Hz,在20Hz～80Hz频段上力限的斜率为2.72dB/oct,在200Hz～2 000Hz频段上斜率为-8.56dB/oct。

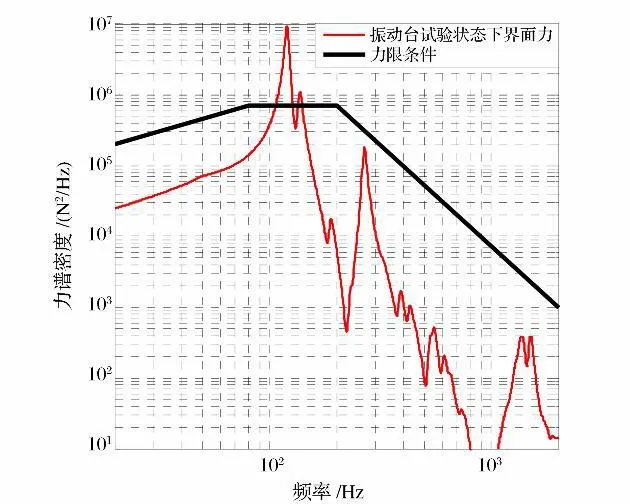
图4为Y 方向振动试验中试验夹具与试验件界面处横向力谱密度与力限条件比较图。在119.7Hz处,界面横向力谱密度为8.16×106N2/Hz,比力限条件高11.0dB。本算例中,振动试验界面力谱曲线和力矩谱曲线是通过对负载的有限元分析得到的。

图5为Y 方向振动试验力矩限计算结果。在中心频率为200Hz 的频段复杂二自由度方法得到的力矩限最大,为9.64×104(N·m)2/Hz。力矩限条件:在80Hz～200Hz频段上力矩限为1.00×105(N·m)2/Hz,在20Hz～80Hz频段上力矩限的斜率为3.49dB/oct,在200Hz～2 000Hz频段上斜率为-9dB/oct。

图5 Y 方向力矩限条件Fig.5 Interface moment limit in Y direction

图6 Y 方向力矩限条件与界面横向力矩谱密度比较图Fig.6 Comparison of moment limit and global Interface moment PSD,Y direction

图7 引入力限时的加速度条件下凹Fig.7 Notching of acceleration PSD with force limit

图8 引入力矩限时的加速度条件下凹Fig.8 Notching of acceleration PSD with moment limit

图6为Y 方向力矩限条件与振动试验界面力矩谱密度比较图。在119.7Hz 处,界面横向力矩谱密度为1.88×106(N ·m)2/Hz,比力矩限条件高

12.7dB。

和传统的振动试验不同的是,力限随机振动试验在监测振动台输入基础激励的同时还将监测界面力和力矩,并在界面力大于力限条件时控制试验输入,使得界面力不超过给定的力限条件。不考虑非线性因素,在进行引入力限和力矩限时的随机振动分析中,加速度输入谱都将在106Hz～130Hz频段下凹,下凹量级可分别达11.0dB 和12.7dB,如图7和图8所示。大量的仿真算例表明,力矩限和力限通常在同一频段限制了加速度谱密度输入,下凹的量级也大体一致。由此可见,用模态有效质量相应非对角线元素构建简化模型,并应用简单二自由度方法、复杂二自由度方法和半经验方法得到的力矩限条件的设计方法是可行有效的。

5 结束语

本文基于模态有效质量概念提出了力矩限设计策略;计算了某航天器有效载荷的力限条件和力矩限条件。通过仿真分析,可以看出力矩限和力限在同一频段达到峰值;在试验件共振频率处,由复杂二自由度方法计算得到的力矩限,要大于简单二自由度方法和半经验方法;力矩限条件设计方法是可行和有效的,可以为今后我国力限振动试验提供技术支持。

在后续的航天器力限试验技术研究中,应重点研究横向界面力控制技术和界面力矩控制技术,并结合工程实际,验证并发展航天器横向力限振动试验的力矩限条件设计技术,提高我国航天器的设计和试验水平。

References)

[1]马兴瑞,于登云,韩增尧,等.星箭力学环境分析与试验技术研究进展[J].宇航学报,2006,27(3):323-331

[2]Scharton T D.Force-limited vibration testing monograph[R].NASA-RP-1403,NASAReport,1997

[3]NASA.Force limited vibration testing[Z].NASA-HDBK-7004B,NASATechnical Handbook,2003

[4]Scharton T D.Vibration-test force limits derived f rom f requency-shif t method[J].AIAAJournal of Spacecraft and Rockets,1995,32(2):312-316

[5]Davis G L.An analysis of nonliear damping and stiffness effects in force-limited vibration for reduction of overtesting[D].Rice University,Houston,US A,1998

[6]李正举,马兴瑞,韩增尧.基于力限的加速度谱下凹技术研究[J].航天器工程,2010,19(4):23-28

[7]金恂叔.航天器动力学环境试验的发展概况和趋势[J].航天器环境工程,2003,20(2):15-21

[8]张俊刚,庞贺伟.振动试验中力限控制技术[J].航天器环境工程,2005,22(5):253-256

[9]张俊刚.航天器振动试验力限控制技术研究[D].中国空间技术研究院,2009

[10]王晓耕.力限技术的发展和应用前景[J].航天器环境工程,2002,19(4):23-26

[11]李正举,韩增尧.力限振动试验力限条件设计方法初探[C]//南昌:中国航天结构强度与环境工程专业信息网2009年度技术信息交流会,2009,9

[12]柳征勇,王皓.星箭力限试验力限条件设计研究[C]//南昌:中国航天结构强度与环境工程专业信息网2009年度技术信息交流会,2009,9

[13]陈凯,黄波.振动系统反共振点力谱预示[C]//南昌:中国航天结构强度与环境工程专业信息网2009年度技术信息交流会,2009,9