一种卫星飞行模拟器的热控分系统模型设计

何 治 许晓冬 赵啟伟

(1 北京空间飞行器总体设计部,北京 100094)

(2 中国空间技术研究院通信卫星事业部,北京 100094)

1 引言

卫星飞行模拟器是一种数字或半物理仿真系统,主要用于卫星地面系统校验、卫星故障模拟与故障辅助诊断、卫星控制策略验证和卫星操控人员培训。随着卫星研制技术的发展,越来越多的卫星公司针对其生产的卫星开发飞行模拟器,例如:美国的GPS 卫星模拟器(1998年)[1]、欧洲的热鸟-7A(HotBird-7A)卫星模拟器(2006年)、鑫诺一号卫星模拟器(1998年)、中星9 号卫星模拟器(2008年)等。近年来,国内研制的卫星也开始搭配飞行模拟器。

根据现有的资料,各种卫星飞行模拟器[1-4]的热控分系统主要是根据试验或飞行数据,基于试验建模技术构建。这种热控分系统模型具有运行速度快,在特定条件下仿真精度高的优点,但对于星内仪器工作模式变化以及卫星外热流变化等情况的仿真能力较差,相应条件下的仿真误差也大大增加。

为了解决上述问题,进一步提高飞行模拟器的仿真能力以及实用性,本文设计了基于偏微分方程的飞行模拟器热控分系统模型,用于仿真卫星内、外热源变化条件下,卫星各个仪器、结构的温度情况。

2 热控分系统体系结构

如图1所示的热控分系统体系结构,本文采用的是星型体系结构。为保证系统的可靠性,卫星模拟器的热控分系统不设计人机交互接口,也不设计与其它分系统之间相连的接口,所有数据的输入和输出都需要通过卫星模拟器数据控制中心转发。

飞行模拟器热控分系统模型主要包含以下几个部分:

1)卫星外热流实时仿真软件

采用基于计算机图形学的消隐算法设计,能够根据卫星姿态、轨道位置以及卫星表面热性质的变化,输出相应的外热流数据。

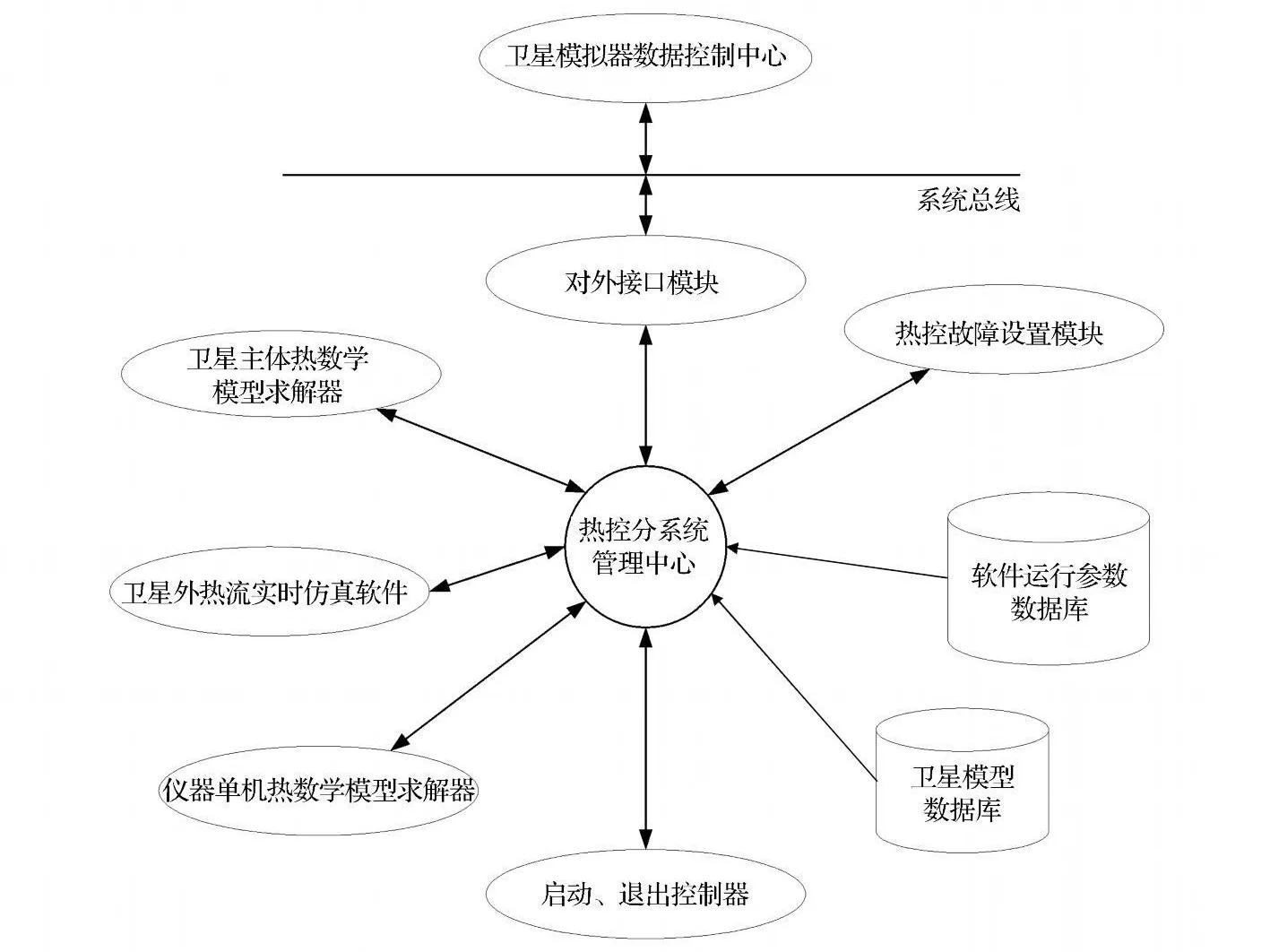
图1 卫星飞行模拟器热控分系统体系结构Fig.1 System structure of thermal control subsystem for f lying satellite simulator

2)卫星模型

卫星主体部分的物理模型通过四边形和圆形节点描述,节点或仪器的热耗、热容,各个节点或仪器之间的换热关系等参数按照节点和仪器编号一一对应。节点的具体数量及相关参数与卫星类型相关,从卫星热分析模型转化而来。

3)卫星数学模型求解

卫星在宇宙空间中运行时,受空间冷黑环境和星体辐射外热流的综合影响,这是卫星仿真的外部条件;对于常用卫星,其传热方式为导热和辐射的耦合换热;此外,卫星内部各种仪器工作模式的变化、各种主动热控手段(主要指加热器),构成了卫星内部热源项。考虑上述各种影响因素给出如下方

程[5-6]:

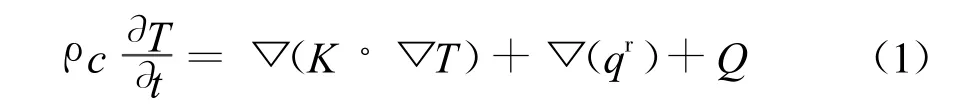
式中,ρ为密度(kg/m3),c为比热(J/kg·K),K为导热系数(W/m·K),T为温度(K),τ为时间(s),qr为辐射热流(W/m2),Q为源项。源项包括内部热源(热耗和加热功率)以及外部热源(外热流)。

对于星上一些热独立性较强的单机设备,采用最小二乘法,根据试验或热分析数据构建经验关系式模型。各模型的基本结构如下。

太阳敏感器、地球敏感器:

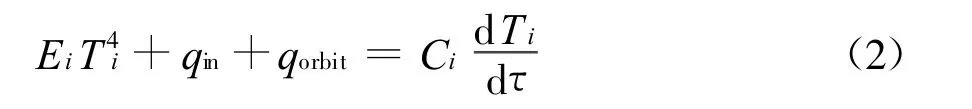
推进剂管路:

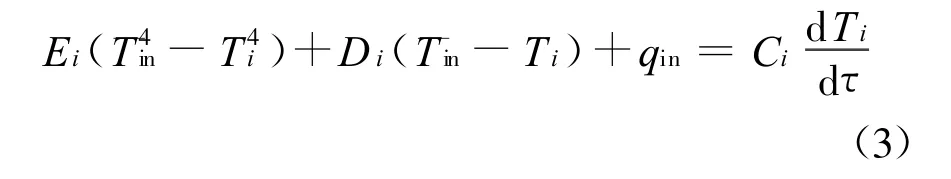
对于部分无法用上述两模型准确表述的仪器,如天线等,直接采用如下关系式描述:

式(2)、(3)、(4)中,i为节点编号,i =1,2,3,…;τ表示时间;Di、Ei、Ti分别表示节点i 与外部的综合导热系数、辐射换热和温度;ˉTin表示卫星内部的平均温度;qin表示节点i 的内部热源;qor bit表示节点i 的外部热流;参数a、b、c、d、e、f为常数。

根据Taylor级数展开法[7],对于方程1 进行差分离散,构建Dufort-Frankel 差分格式,对于任意节点i(i=1,2,3,…),有:

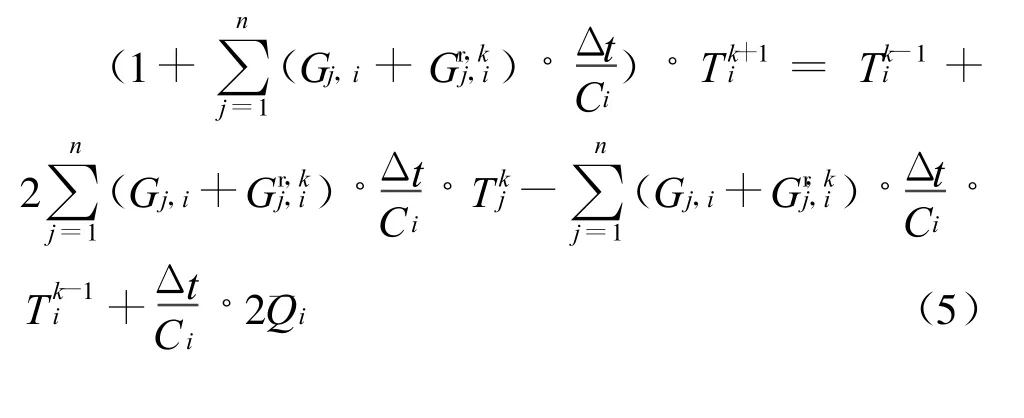
此外,k为时间步(k =0,1,2,3,…),C为热容(J/K),v为容积(m3),Eji为节点i 与节点j 间的辐射换热系数,根据卫星的热分析模型确定,Gi,j为节点i、j 之间的线性导热(W/K),l为节点之间的距离(m),A为垂直于导热方向上的面积或辐射面积(m2),Gr为辐射导热(W/K),Δt是自变量τ的改变量。

可以证明,式(5)相容于原方程(1),是绝对稳定[8-10]并且收敛。

4)热控分系统模块运行控制与管理

采用专门软件模块对热控分系统模块的运行进行集中控制和管理,动态的处理和校核热控分系统输入、输出数据。

3 热控分系统运行描述

1)运行模式

如图2所示,卫星模拟器系统通过网络与地面测控站的控制中心计算机进行交互,卫星模拟器产生遥测数据给控制中心计算机,控制中心计算机发送遥控指令用于控制卫星模拟器运行。

与此相应,热控分系统也有两种运行模式,其一是由控制中心计算机发送指令控制,用于仿真正常运行过程中对卫星的各种操作;其二是由飞行模拟器控制,用于启动、暂停和停止热控分系统的运行,以及修改热控分系统的各种参数,仿真卫星各种与热控分系统相关的故障。

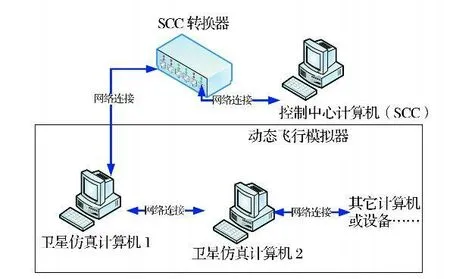
图2 卫星飞行模拟器运行过程系统组成Fig.2 Running system of flying satellite simulator

2)热控分系统的运行过程

卫星飞行模拟器启动后,由模拟器数据控制中心决定是否启动热控分系统。仿真过程中,热控分系统根据数据控制中心的输入参数,执行相应的动作。

图3所示是热控分系统的运行流程。热控分系统运行过程比较复杂,涉及仿真数据在模型内部各部分之间的相互交换,图4示出了飞行模拟器热控分系统的仿真数据流,该图主要表示仿真数据的流向,并非真实路径。实际上,各个模块之间是不能直 接通信的,必须通过热控分系统管理程序转发。

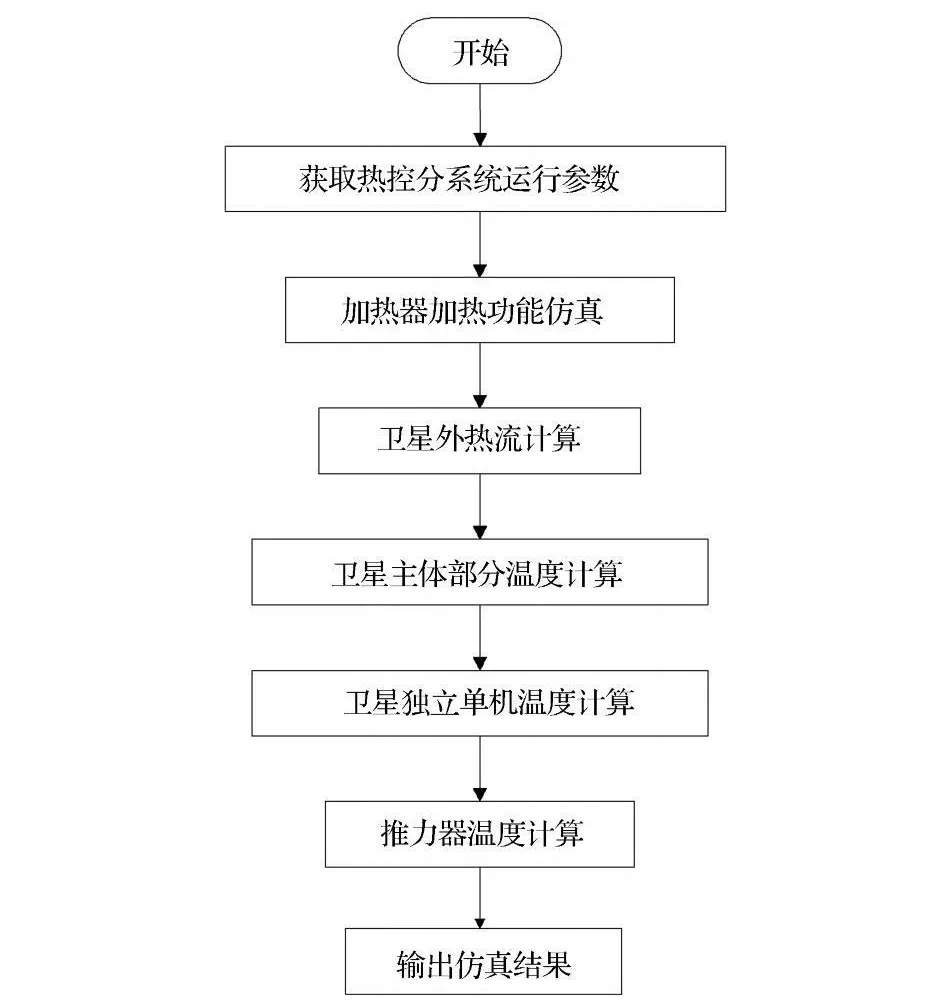
图3 卫星飞行模拟器热控分系统运行框图Fig.3 Block diagram of running of thermal control subsystem for flying satellite simulator

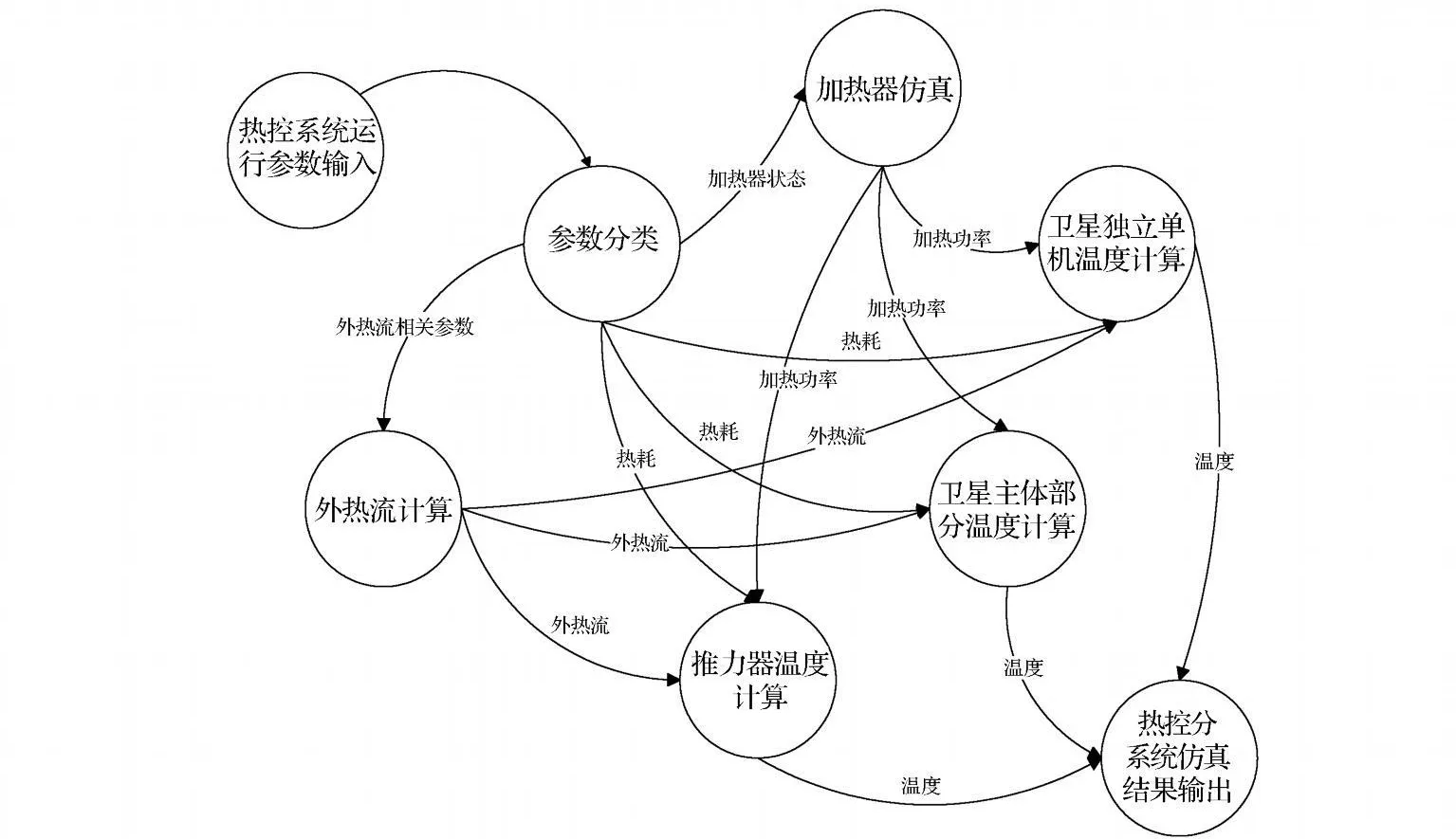
图4 卫星飞行模拟器热控分系统运行数据流图Fig.4 Data flow diagram of running of thermal control subsystem for flying satellite simulator

4 性能和功能验证

根据某型通信卫星,完成飞行模拟器热控分系统的具体实现。完成后,卫星的热控分系统模型具有近2 500个节点,各个节点之间换热关系的总数超过25 万。

1)实时性

虽然模型结构复杂,但是热控分系统的运行速度仍然能够达到8倍速(即在1s 内完成未来8s 卫星温度数据的输出),具备实时性。

2)对卫星指令的响应功能

通过打开加热器来测试卫星模拟器热控分系统对卫星指令响应的仿真功能,测试的内外热源条件任意选择。如图5、图6所示,在寿命初期春分时,在1时刻打开遥测点T108(遥测点代号,具体物理意义略,下同)和T110 附近的加热器直到2时刻关闭。遥测点T108 和T110 受加热器的影响,温度遥测发生显著变化。

之后,为了测试其它加热器的功能,又陆续打开或关闭多个加热器,因此,测点T108 和T110 的温度会偏离没有加热器打开时的温度曲线,呈现无规律变化。大约到卫星时48h 的时候,不再继续进行加热器功能试验,这两个测点的温度开始逐渐有规律变化,并趋向于周期性稳定状态。

3)仿真精度

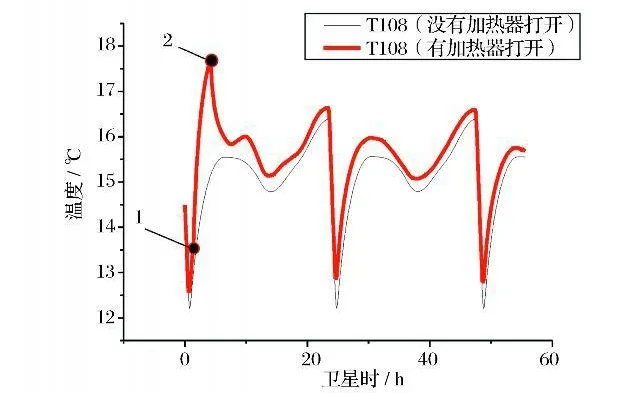
图5 测点T108 的温度Fig.5 Simulation results of T108

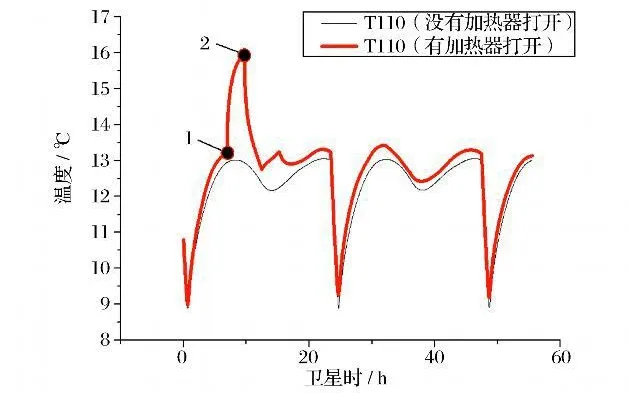
图6 测点T110 的温度Fig.6 Simulation results of T110

除了采用经验关系式(2)、(3)、(4)描述的太阳敏感器、地球敏感器、天线等设备,其它采用式(5)描述的卫星主体部分结构及设备,热控分系统输出的温度数据与其它热分析软件的计算结果相比较,偏差都能保持在±3℃内,绝大部分结果的偏差小于±1℃,如图7和图8中随机抽取的测试结果。

图7 测点T7 的温度Fig.7 Simulation results of T7

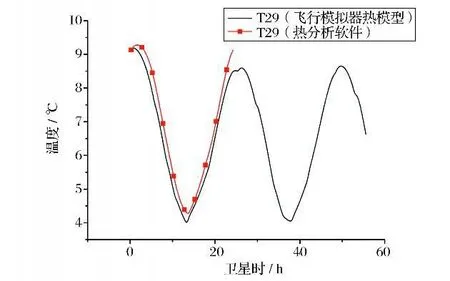
图8 测点T29 的温度Fig.8 Simulation results of T29

采用卫星飞行模拟器热控分系统对相同条件下卫星在轨温度情况进行仿真,仿真结果如图9和图10所示。在这里,卫星模型的天线等设备采用单机模型,并未集成在卫星本体模型中,由于这些单机设备的简化对卫星本体部分的外热流计算有影响,因此对仪器温度的仿真结果有一定影响,所以在仿真值与飞行数据之间存在一定差异。

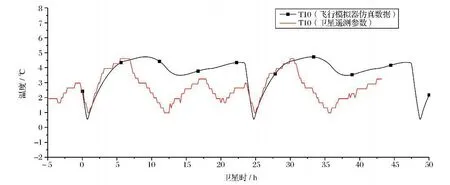
图9 测点T10 的仿真结果与卫星飞行数据比较Fig.9 Simulation results vs.in-orbit data of T10

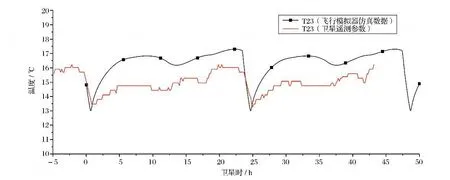
图10 测点T23 的仿真结果与卫星飞行数据比较Fig.10 Simulation results vs.data in orbit of T23

4)故障仿真

以热管故障来演示热控分系统的故障仿真功能。图11是热管故障发生前后热管两端仪器上测点的温度仿真值。故障发生前两仪器之间的温差约为2.5℃,仿真8 500s时,热管发生故障,热管的温度拉平作用减小或消失,使得一端仪器A的温度降低,另一端仪器B 的温度升高,最后导致两仪器的温差达到约6℃。

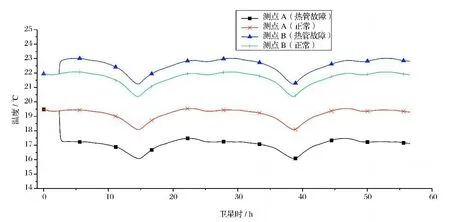
图11 热管故障演示Fig.11 Demo of heat-pipe fault

5 结束语

本文通过构建基于偏微分方程的热控分系统模型,实现了对卫星在轨温度遥测数据的实时仿真。并将仿真结果与相同条件下卫星热分析结果和卫星在轨温度遥测数据进行了比较,比较结果表明,构建基于偏微分方程的热控分系统模型,能够在仿真功能上实现设计目标,可以仿真卫星在各种外热流、内热源组合条件下的温度情况,也能够对与热控分系统相关的各种故障进行仿真,同时具有较高的仿真精度、速度。本文提出的方法可以用于卫星飞行模拟器热控仿真系统设计。

References)

[1]Mark B,Dingman B,Gregg W.High fidelity GPS satellite simulation[R].AIAA-1997-3671,1997

[2]M ark B.High fidelity GPS satellite simulator-Atraining tool[R].AIAA-1999-4119,1999

[3]Mark B.H igh fidelity GPS satellite simulation results[R].AIAA-1998-4375,1999

[4]Morris C,Rothwell D.Operational spacecraf t simulations present and future[C]//Simulation and Modelling of Satellite System s,IEEE Seminar and Exhibition,2000

[5]Tsai J R.Thermal analytical formulations in various satellite development stages[R].AIAA-2002-3018,2002

[6]Tsai J R.Overview of satellite thermal analytical model[J].Journal of Spacecraf t and Rockets,2004,41(1):120-125

[7]Collins R L.Afinite difference Taylor series bethod Applied to Thermal Problems[R].AIAA-88-2664,1988

[8]徐长发,实用偏微分方程数值解法[M].武汉:华中理工大学出版社,1990

[9]廖晓昕.稳定性的数学理论及应用[M].武汉:华中师范大学出版社,2001

[10]颜敏娟,卢殿臣,田立新.一类非线性抛物方程的隐式解法及外迭代收敛性[J].江苏大学学报(自然科学版),2003,24(3):17-19