一类二阶微分方程数值新算法

谭加博,蔡成伟

(北京物资学院信息学院,北京 101149)

一类二阶微分方程数值新算法

谭加博,蔡成伟

(北京物资学院信息学院,北京 101149)

通过辛Euler数值算法的构造过程的研究,在发现构造辛Euler法格式的同时,还有另外的两个相似性质的算法格式,对这两种算法格式的研究以及与辛Euler算法的比较,得出数值算法优秀的标准以及优秀数值算法形成过程中需要改进的方向.通过摆方程比较这些数值算法实际的计算效果,得知辛Euler算法格式优于其他两种相似性质的算法格式.

二阶微分方程;时间代价;辛Euler法;新数值算法;摆方程

0 引言

通过对一阶微分方程的Euler算法、改进Euler算法、隐Euler算法、Gauss中点算法以及对二阶微分方程的数值解法辛Euler法的研究,发现在一阶微分方程这组算法中,用于计算二阶微分方程的数值算法的辛Euler算法是由Euler算法和隐Euler算法组合而成.于是在研究辛Euler法的同一理论平台上,笔者提出了一个由Euler算法和Gauss中点算法组合或者是由Euler算法和改进Euler算法组合而成的新算法,并对这两种新组合方法在求解二阶微分方程中运用,与目前流行的辛Euler法做比较,从而发现所给新算法的优缺点.

1 4种基本数值算法的格式推导

其中u0是给定的初值,这就是一阶常微分方程的初值问题.为使问题(1)的解存在、唯一且连续依赖初值即初值u0问题(1)适定,还必须对右端f(t,u)加适当限制,通常要求f关于u满足Lipschitz条件:即存在常数L,使

对所有t∈[0,T]和u1,u2∈(-∞,∞)成立.在常微分方程数值解法中,对于常微分方程初值问题的数值解法都要满足上述的Lipschitz条件[1].

1.1 Euler法

最简单的数值解法是Euler法.将区间[0,T]作N等分,小区间的长度h=T/N称为步长,点列tn=nh(n=0,1,2,…,N)称为节点,t0=0由已知初值u(t0)=u0,可算出u(t)在t=t0的导数值u′(t0)=f(t0,u(t0))=f(t0,u0).利用Taylor展式

其中ζ∈(t0,t1),并略去二阶小量R0,得u1=u0+hf(t0,u0).u1就是u(t1)的近似值.利用u1又可算出u2,如此下去可算出u在所有节点上的值,一般递推公式为

这就是Euler法[2].

1.2 改进Euler法

下面对Euler法运用数值积分法推导.将问题(1)写成等价的积分形式

特别地

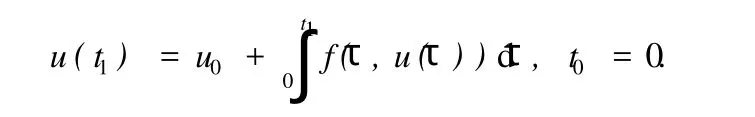
用左矩形公式近似右端积分,并用u1替代u(t1),即得u1=u0+hf(t0,u0),这就是Euler法(式(5)).我们也可用梯形公式近似上述积分,仍用u1替代u(t1),得

称之为改进Euler法[2].

1.3 隐式Euler法

隐式Euler法[3]同Euler法的数值解法相似,将区间[0,T]作N等分,小区间的长度h=T/N称为步长,点列tn=nh(n=0, 1,2,…,N)称为节点,t0=0是已知初值u(t0)=u0.在Euler法中,数值计算的迭代格式中运用初始值点(t0,u0)进行格式迭代计算.在改进Euler法中,数值计算的迭代格式中运用初始值点(t0,u0)和所求值点(t1,u1)进行格式迭代计算.根据上面的Euler法和改进Euler法的格式推导过程可以进行相似的演变.将Euler法中迭代点(t0,u0)用所求值点(t1,u1)代替,因此有数值计算的迭代格式

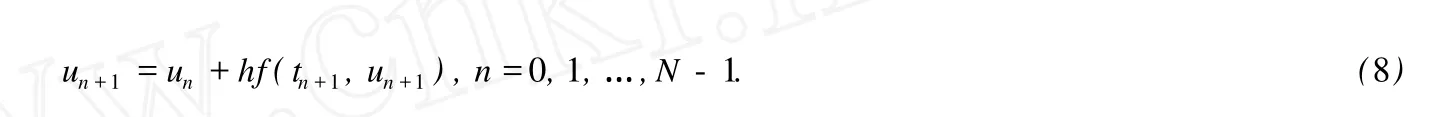
1.4 Gauss中点法

对于问题(1)上面3种数值算法都可求解,但是,这样的求解结果并没有得到微分方程数值解研究者的满足.我们需要得到更好的数值算法.Gauss在对上述的3种数值算法反复研究后,再次改造Euler算法的算式格式.将运用迭代格式中相邻2点的中点作为算式的迭代值,即取t=0初始点(t0,u0)与后一点(t1,u1),将这2点的中点((t0+t1)/2,(u0+u1)/2)作为Euler法格式中的迭代点.即,这个中点迭代格式为

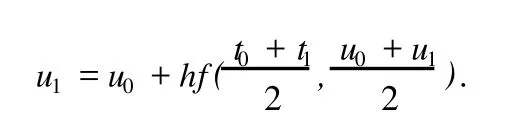
在一般情况下,将区间[0,T]作N等分,小区间的长度h=T/N称为步长,点列tn=nh(n=0,1,2,…,N)称为节点,迭代格式为

这个迭代格式就称为Gauss中点法[3].

2 辛Euler算法推导以及误差估计、局部稳定性

通过4个基本数值算法,得到一阶微分方程的数值求解.但是,对于二阶微分方程

的数值解,通过一阶微分方程的数值算法思想知道可将二阶微分方程化为两个一阶微分方程来求数值解.在此假设令y′= w(x,y),对二阶微分方程(10)可以化为

通过求解一阶微分方程组来求解这个二阶微分方程.应用上面的4种基本数值算法来求解一阶微分方程组.

通过上述的微分方程转化后,将Euler法和隐Euler法应用到二阶微分方程化成的两个一阶微分方程中.将微分方程组(11)中的第一个微分方程用隐Euler法求数值解,第二个微分方程用Euler法求数值解,然后将两个数值解格式合并在一起后的数值算法格式,称为辛Euler法[1].由于辛Euler算法是在局部稳定性算法的基础上组合而成,同时微分方程也是满足Lipschitz条件,所以辛Euler数值算法也是局部稳定.对于上面的二阶微分方程,假设在数值算法中,将Euler算法和隐Euler算法的迭代步长相等为h代入,得数值算法格式推导过程如下.

格式(12)为辛Euler法的通式.

将二阶微分方程的真解,应用泰勒展开式展开后有

可以看出,辛Euler法的局部截断误差en的阶次为O(h3).辛Euler法的整体截断误差εn的阶次为O(h2).

通过辛Euler算法的误差估计可知,辛Euler法也是收敛的.在此延续前面的假设条件,对于辛Euler法的格式(12)的局部稳定性研究如下

在这里L,h,e0都是常数,所以可以知道辛Euler法是局部稳定的.同时,辛Euler法是显示格式.

3 另外两种数值算法以及误差估计、局部稳定性

在辛Euler法的推导中,可以知道,在辛Euler法产生的算法理论平台上,除了有Euler法与隐Euler法可以组成显示迭代格式外,还有另外的两种基本算法的组合方式也能形成显示迭代格式.在这两种组合方式中,一个算法是由Euler法与改进Euler法组合而成;一个算法是由Euler法与Gauss中点法组合而成.这3种数值算法都是同一个算法理论平台中的显示格式.从前面的辛Euler法中可以知道,这两种算法也是收敛的.

3.1 第一种数值算法

在二阶微分方程数值求解中,将Euler法与改进Euler法组合而成.对于二阶微分方程(10)问题的求解,将其转化为一阶微分方程组(11)的形式.在此借用辛Euler法中的假设条件,将第一个一阶微分方程用改进Euler法格式,第二个一阶微分方程用Euler法格式,故有此数值算法的格式推导如下

这个格式就是第一种数值算法的格式.第一种数值算法格式与辛Euler法的格式在最后一部分上系数不同.

将二阶微分方程的真解,应用泰勒展开式展开后有

可以看出,第一种数值算法的局部截断误差en的阶次为O(h3).通过改进Euler法的结论可以知道第一种数值算法的整体截断误差εn的阶次为O(h2).

通过上面的第一种数值算法的格式与二阶微分方程真解的展开格式相比可见,前者更加接近真解.第一种数值算法的格式与真解的展开式的前面3部分值完全相同.在它们误差相当的情况下,从数值算法的格式中可见,第一种数值算法在构造的迭代格式上比辛Euler法要更精确些.

第一种数值算法在此延续前面的假设条件,对于第一种数值算法的格式(13)的局部稳定性[3]研究如下

在这里L,h,e0都是常数,所以第一种数值算法格式是局部稳定的.

3.2 第二种数值算法

在二阶微分方程数值求解中,将Euler法与Gauss中点法组合而成.对于二阶微分方程(10)问题的求解,将其转化为一阶微分方程组(11)的形式.在此借用辛Euler法中的假设条件,将第一个一阶微分方程用Euler法格式,第二个一阶微分方程用Gauss中点法格式,有这个数值算法的格式推导如下

将真解的展开式同第二种数值算法的迭代格式的转化形式(18)相比较,第二种数值算法格式的局部截断误差en的阶次为O(h3),整体截断误差εn的阶次为O(h2).

第二种数值算法的迭代格式在形式上比辛Euler法的迭代格式更加复杂,所以在数值计算时需要的初始条件更多.与辛Euler法相比,在误差上相当.从数值算法的构造迭代格式上来看,辛Euler法要好于第二种数值算法.

第二种数值算法在此延续前面的假设条件,对于第二种数值算法的格式(14)的局部稳定性研究如下

这里L,h,e0都是常数.从上面的不等式可知,第二种数值算法格式的局部截断误差en是有上限的,且由前面的两步迭代截断误差决定,所以第二种数值算法格式具有局部稳定性[3].

4 3种二阶微分方程数值算法的实验比较

衡量算法的时间代价也是评价一种算法的指标,所以,对于数值算法的研究,必须通过计算机的实际检验.同时,对于算法的整体稳定性也是通过算法的实际计算得到的结果.

对于二阶微分方程的数值算法中选择的辛Euler算法,以及在同一个算法的理论平台中,还有另外两种数值算法,它们都是显示算法格式.同时,通过算法的实验,也能够很好地直观地感觉算法的精确性、稳定性.为了算法实验获得更直观的感受,将算法通过摆方程来实验,摆方程在实际的计算中有很好的视觉效果.在算法实验前,先假设摆方程的初始问题如下

在此,假设q′=p,则摆方程化成一阶微分方程组有

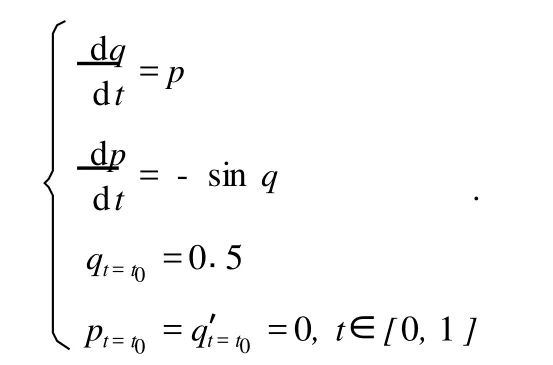
在摆方程的两个一阶微分方程的数值计算中,假设两个微分方程的数值计算步长相同,设为h.迭代计算的总步长数,设为N,则n=0,1,…,N.其中,将摆方程问题的初始值是t=0的值记为p0=0,q0=0.5.在算法实验中,为了知道算法的运算时间代价,将算法的运算完成的时间记为T.

4.1 辛Euler法摆方程实验算式格式

对于摆方程初始值问题(19)在辛Euler法中的实验,由辛Euler法的格式和初始值的摆方程问题有实验的算法迭代格式

4.2 第一种数值算法摆方程算式格式

对于摆方程初始值问题(19)在第一种数值算法中的实验,由第一种数值算法的格式和初始值的摆方程问题有实验的算法迭代格式

4.3 第二种数值算法摆方程算式格式

对于摆方程初始值问题(19)在第二种数值算法中的实验,由第二种数值算法的格式和初始值的摆方程问题有实验的算法迭代格式

下面对3个算法的摆方程问题数值计算运用不同的步长h,不同的迭代步长数N编程,并将运行结果以图像的形式显示[4].

4.4 3种数值算法整体稳定性比较分析

在h=0.1,N=400时3种数值算法的计算结果如图1.可见,第二种数值算法的整体稳定性是不好的,在迭代不到400步就向负方向飞出.在h=0.1,N=900时3种数值算法的计算结果如图2,可知第一种数值算法在迭代接近900步时,算法的迭代数值就飞离了,所以第一种数值算法的整体稳定性也不是很好.从3种数值算法的摆方程的7个计算结果图中能够很明显地看出,第一种数值算法和第二种数值算法的迭代运算值是向外扩散的,而辛Euler法的迭代运算值一直很稳定地保持在一条线带上,所以辛Euler法的整体稳定性比另外两种数值算法好.

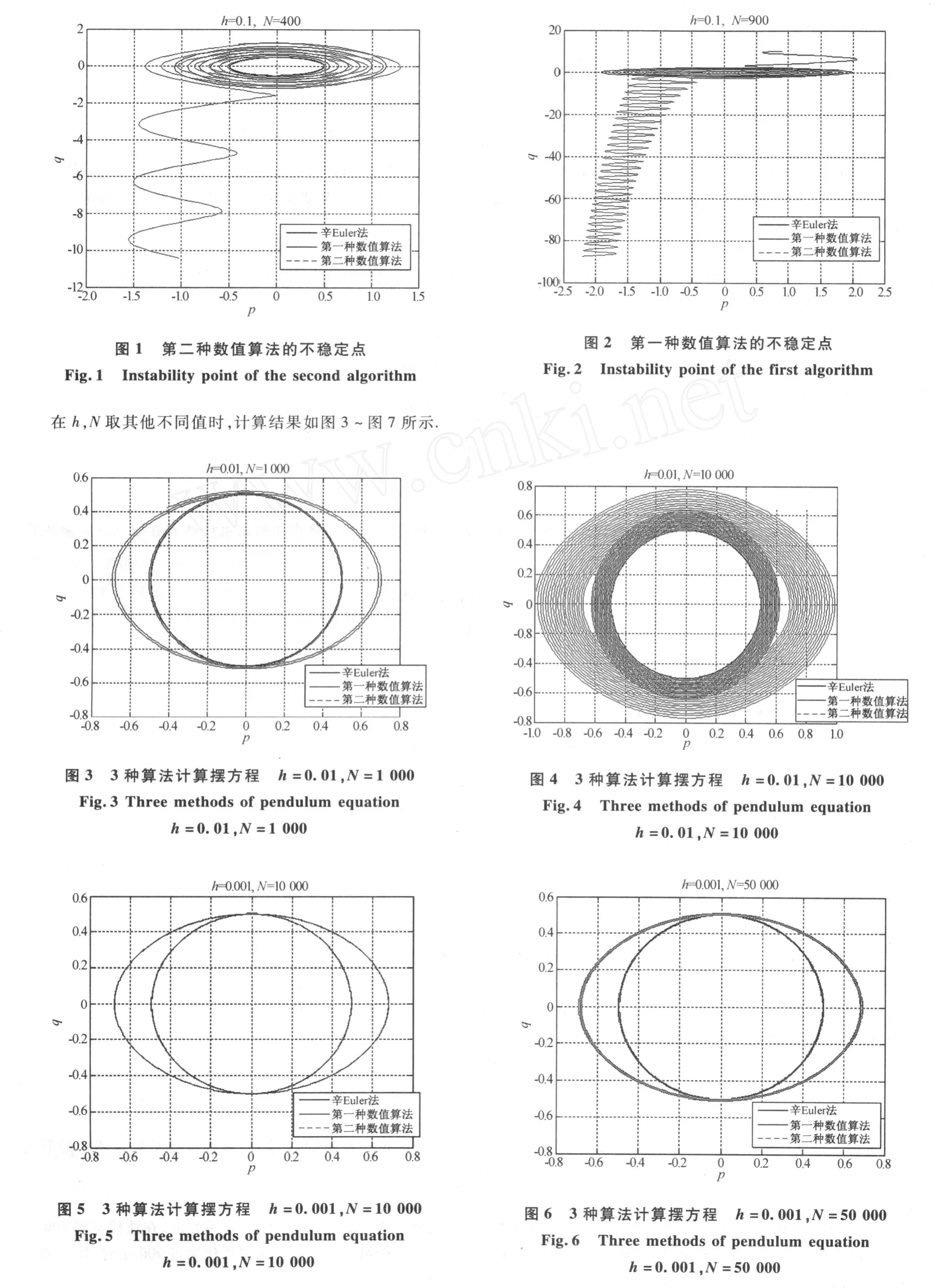
图7 3种算法计算摆方程 h=0.001,N=100 000Fig.7 Three methods of pendulum equation h=0.001,N=100 000

4.5 3种数值算法的时间代价

在实验中,通过在同一台计算机上进行3种数值算法计算同一个摆方程的实验,同时在相同的计算机环境下平衡实验的系统误差,去除实验的偶然误差,对算法运算的计时知道,在步数N<10 000时,都能够很快地完成,对于步数N>10 000时,都需要一段时间才能够得到结果.可见3种算法的运算时间相当.

5 结论

在对辛Euler法、第一种数值算法、第二种数值算法进行摆方程实验之前,通过理论的分析比较知道3个数值算法在算法的理论上的收敛性、局部稳定性、误差估计3个方面都是相当的.从算法的表面迭代格式上看,由Euler法和改进Euler法组合而成的第一种数值算法的迭代格式要比辛Euler法的迭代格式更好一些.首先,在算法实际迭代出算法格式的过程中,辛Euler法要比另外两种算法更好,辛Euler法是构造迭代格式最简单的算法,其次是第一种数值算法,最后是第二种数值算法.尽管3种数值算法在理论上相当,但是在这3种数值算法的摆方程实验中,可知辛Euler法具有很好的整体稳定性,另外两种数值算法的整体稳定性不好,只是第一种数值算法的稳定性比第二种数值算法的稳定性要好一些.另外,3种数值算法的时间代价都是相当的.综上所述,可知辛Euler法比另外两种数值算法更好,更加具有实际应用的价值.

[1] 余德浩,汤华中.微分方程数值解法[M].北京:科学出版社,2004.

[2] 李荣华,冯果忱.微分方程数值解法[M].3版.北京:高等教育出版社,1995.

[3] 戴嘉尊,邱建贤.微分方程数值解法[M].南京:东南大学出版社,2003.

[4] 毛涛涛,王正林,王玲.精通MATLAB GU I设计[M].北京:电子工业出版社,2008.

A New Algorithm for Second Order D ifferential Equations

TAN Jia-bo,CA ICheng-wei
(College of Info rm ation,Beijing W uzi University,B eijing101149)

Finds another two similar algorithm formats while constructing symplectic Euler method format through studying the process of symplectic Euler numerical algorithm.Comparing these two for mats with symplectic Euler method,finds the standard of an excellent numerical algorithm and the approach of improving such excellent numerical algorithm.By pendulum equation compares the numerical algorithms.Proves that the symplectic Euler algorithm format is better than the other two similar algorithm for mats.

second order differential equation;time cost;symplectic Eulermethod;new numerical algorithm;pendulum equation

O175.1

A

1007-0834(2011)01-0016-08

10.3969/j.issn.1007-0834.2011.01.007

2010-04-13

北京市优秀教学团队——“数学公共基础系列课程教学团队”支持项目(PHR200907230)

谭加博(1982—),男,黑龙江鸡西人,北京物资学院信息学院讲师,理学博士.