地面搜索路径的“S式”折线模型和螺线模型
2011-12-25刘晓妍吕濯缨高国成
刘晓妍,吕濯缨,高国成
(山东科技大学公共课部,山东济南 250031)
地面搜索路径的“S式”折线模型和螺线模型
刘晓妍,吕濯缨,高国成
(山东科技大学公共课部,山东济南 250031)
2008年全国大学生数学建模竞赛C题是关于汶川大地震的地面搜索问题.为寻找用时最短的搜索路径,主要从缩短不搜索时的行进路线考虑,建立了“S式”折线模型和螺线模型,并对模型结果进行理论验证,其中螺线模型的方法构思巧妙,结果合理且较优.
地面搜索;曲线积分;“S式”折线模型;螺线模型
1 问题重述
需要解决的问题是:震后受灾地区地面搜索路线设计问题.通过对搜索问题[1-2]的简化,确定了1个大小为11 200 m×7 200 m的平面矩形目标区域(如图1).搜索过程的条件及要求如下:
(1)以区域中心O为出发点,搜索完成后,搜索队伍在左侧短边中点P处集结;
(2)每个人的可探测半径为20 m,搜索时行进速度为0.6 m/s,无需搜索时行进速度为1.2 m/s;
(3)搜索队伍若干人为1组,每组有1名组长;
(4)设备配置情况为:GPS定位仪每人1台,步话机每人1部(通信半径为1 000 m),组长配有卫星电话1部.搜索过程中,每个人搜索到目标,都需要用步话机及时向组长报告,组长再用卫星电话向指挥部报告搜索的最新结果.
问题 有1支20人1组的搜索队伍,拥有1台卫星电话.需要设计1种耗时最短的搜索路径,并求出搜索完整个区域的时间.看能否在48 h内完成搜索任务,若不能,需要增加多少人才可在48 h内完成搜索任务.
2 模型假设
(1)假设搜索区域内任2点之间都可直线抵达,即行进过程中无障碍物抵挡;
(2)假设搜索过程中,搜索人员一直处在行进状态中,不会因通话或其他情况而延误时间;
(3)假设搜索过程中2队员间距始终保持40 m不变.

图1 搜索区域Fig.1 Searching area
3 模型建立和求解
3.1 “S式”折线模型
3.1.1 思路分析
根据题意给出如下搜索方式:搜索队员统一行动,站成1排,一起平移.每个队员互相间隔40 m,则最远两队员之间间隔为760 m,在步话机通信半径1 000 m内,而1排队员横向探测距离可达800 m.考虑用“S式”折线型搜索路线,搜索队行进路线如图2.
首先直接从O点徒步到A点,在行进过程中队员边走边散开排成1排,待全体队员到达后一起向B搜索,而后转弯沿“S式”折线行进.由矩形边长7 200 m可知,搜索队员共走了9行及8段转弯距离,最终队员一起走到C处,然后徒步走到终点P.其中,搜索队员在边界上转弯时每人要徒步直线行进800 m.
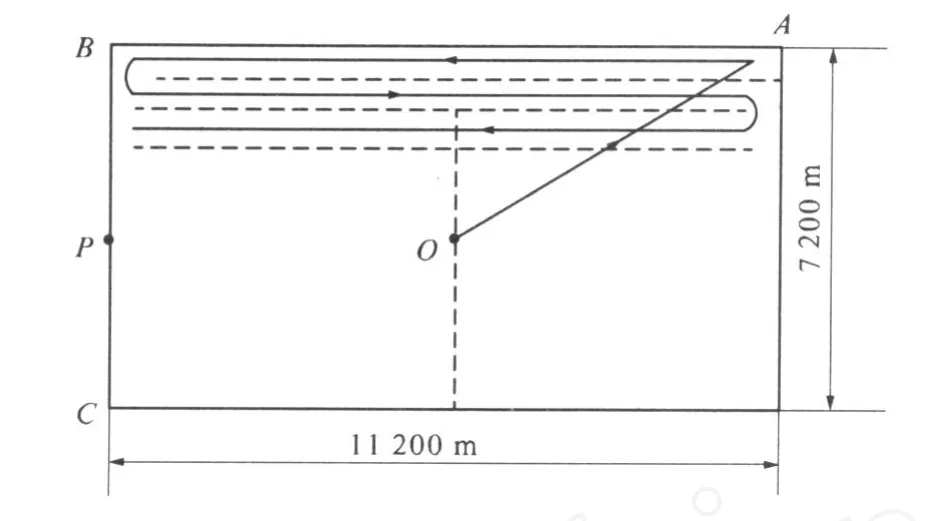
图2 “S式”折线型搜索路线Fig.2 “S-style”broken l ine searching path
3.1.2 模型的建立与求解

3.1.3 结果检验

3.2 螺线模型
3.2.1 思路分析
由于“S式”折线模型中的多处转弯平移浪费时间,故考虑搜索队员沿某连续曲线从中心向外进行搜索时,搜索完整个矩形区域的用时情况.因每个人搜索时的可探测半径为20 m,20人一字排开可探测的横向距离为800 m,此距离在步话机通信半径1 000 m之内,所以可让20人沿等距螺线ρ=aθ向外依次放大搜索.为满足要求,螺距2πa应接近于800 m,于是有2πa=800 m可得a≈127 m.若在中心处就按螺线搜索,重复路径较多,因此先在400 m×800 m的范围内沿直线搜索,后从θ=处向外沿螺线ρ=127θ搜索.搜索至θ=10π后再进入右侧未搜索区域,按“S式”折线型搜索,搜索完成后进入螺旋线左侧未搜索区域仍按“S式”折线型搜索,最后回集结点.
3.2.2 模型建立与求解
(1)模型准备
为描述方便,借助平面螺线的参数方程,利用Mathematic作图[3],将矩形搜索区域分成4部分进行讨论(图3).
区域Ⅰ:400 m×800 m的矩形区域,位于整个搜索区域中心部分(注:螺线所在坐标系的坐标原点位于搜索区域中心上方200 m处);
区域Ⅲ:螺旋线区域右侧1 600 m×7 200 m的矩形区域;
区域Ⅳ:螺旋线区域左侧2 000 m×7 200 m的矩形区域.
(2)模型建立

图3 螺线模型搜索路线Fig.3 Spiralmodel searching path
搜索队伍从O点徒步行至中心矩形区域左边界,一字排开向右搜索400 m至区域Ⅰ右边界,完成区域Ⅰ的搜索;然后于θ=处沿螺旋线搜索至A处(θ=10π),完成区域Ⅱ的搜索;从A徒步沿直线至B,向下搜索7 200 m至整个区域下边界,再折向上搜索7 200 m至整个区域上边界C处,完成区域Ⅲ的搜索;从C处沿直线徒步至D处,行程11 200-2 000=9 200 m,D处距左边界2 000 m,从D处向下搜索至整个区域边界,再折向上搜索至上边界E处,由于E处距左边界400 m,因此将搜索队员平均分为2组,分别记为甲组和乙组,让2组队员同时出发,甲组先搜索1 800 m后徒步行进1 800 m,而乙组则先徒步行进1 800 m后搜索1 800 m,对于剩下的区域甲乙组重复上述过程,同一时间到达F点后2组再一起徒步行进3 600 m到达集结点P处,从而完成区域Ⅳ的搜索.
(3)模型求解

3.2.3 结果检验
由3.1.3知,搜索时间下限为46.67 h,由于螺线模型的结果48.73 h大于46.67 h,故该模型具有一定的合理性和可行性,同时该模型的结果较“S式”折线模型的结果(50.52 h)改进很多.
3.3 增加人数的确定

4 模型评价
(1)模型优点 通过一些合理的假设,采用了由简单到复杂、逐步深入的方法进行分析,建立“S式”折线模型和螺线模型,其中采用螺线模型进行搜索的方法构思巧妙.
(2)模型不足 螺线模型中对螺线区域的4个边角处的搜索进行了忽略,故搜索区域不能覆盖整个目标区域,对结果必然产生一定的影响.
(3)模型推广 以上模型可广泛应用到大规模的农业播种收割、广场的清洁工作等,能够提高工作效率.
[1] 姜启源.数学模型[M].2版.北京:高等教育出版社,1993.
[2] 叶其孝.大学生数学建模竞赛辅导教材[M].长沙:湖南教育出版社,1997.
[3] 万福永,戴浩晖.数学实验教程[M].北京:科学出版社,2003.
“S-Style”Broken L ineModel and SpiralModel About Ground Searching Path
L IU Xiao-yan,LV Zhuo-ying,GAO Guo-cheng
(Depar tm ent of Public Courses,Shandong University of Science and Technology,Jinan250031,China)
The question C in 2008 NationalUndergraduateMathematicalContest inModeling is about theWenchuan Earthquake ground searching problem.To find the search path with the shortest time,mainly consider to shorten the route of non-searching,establish“S-style”broken line model and spiralmodel,and verify the models theoretically:spiralmodel is ingenious and its result is reasonable and better.
ground search;curve integral;“S-style”broken line model;spiralmodel
O141.4
A
1007-0834(2011)01-0007-03
10.3969/j.issn/1007-0834.2011.01.003
2010-10-26
山东科技大学教育教学研究“群星计划”资助项目(QX102175)
刘晓妍(1976—),女,山东威海人,山东科技大学公共课部讲师.
