基于梯度径向夹角直方图的异源图像匹配

李 壮,雷志辉,于起峰

国防科学技术大学航天与材料工程学院,湖南长沙410073

基于梯度径向夹角直方图的异源图像匹配

李 壮,雷志辉,于起峰

国防科学技术大学航天与材料工程学院,湖南长沙410073

提出一种图像全局特征描述方法——梯度径向夹角金字塔直方图。该特征不受图像灰度级非线性变换和图像旋转的影响,具有较强的抗噪声能力。基于该特征的匹配算法能够对存在旋转变换的异源图像进行匹配。用SAR图像和可见光图像对匹配算法进行测试,结果表明基于梯度径向夹角金字塔直方图匹配方法的匹配成功率优于传统方法。由于对基准图进行离线预处理,同时避免角度空间搜索,算法的实时计算时间比传统方法小3个数量级。

异源图像;图像匹配;旋转不变;梯度矢量;径向矢量;金字塔直方图

1 引 言

由不同类型传感器获得的图像被称为异源图像。由于不同传感器间的成像特性存在差别,同一场景在异源图像上可能呈现完全不同的图像,因此传统的同源图像匹配方法一般无法直接应用于异源图像。

国际上主流的异源图像匹配方法可以分为两大类,基于特征的匹配方法和基于区域的匹配方法。基于特征的匹配方法包括特征提取、特征描述、特征匹配三个步骤。理论上,基于特征的匹配方法对图像变形有较好的适应性,但是在异源图像中提取同名特征本身也是一个难题,目前的算法通常都只是针对某类图像有效,而对于噪声污染严重的图像如SAR图像等,尚无较好的同名特征提取方法。传统的特征描述方法有小波特征[1]、形状上下文[2]、矩方法[3]、SIFT[4]、PCASIFT[5]、SURF[6]等,文献[7]中对不同的特征描述方法进行了分析和比较。这些特征描述方法只适用图像描述区域较小,内容简单,区域统计特性明显的情况。例如SIFT特征的有效描述区域在几十个像素内,且要求该区域内有较明显的主方向。由于异源图像提取的特征存在大量非同名点,因此传统的特征匹配方法的有效性也难以保证。

基于区域的匹配方法通常将整幅图像或图像子区[8]的灰度或梯度信息进行匹配。此类方法中利用了图像的所有的空间信息和灰度信息,抗噪性较基于特征的方法更高。常用的基于区域的匹配方法包括灰度互相关方法[9]、梯度相关方法[10]、互信息方法[11],这些方法的主要缺点是对图像旋转及灰度变化比较敏感,另外,由于计算相似度时需要用到全部像素信息,因此计算量也比较大,尽管有优化的匹配空间搜索策略[11-12],其优化后的时间仍难满足实时性的要求。

基于区域的匹配方法能够克服局部噪声,而基于特征的匹配方法能够适应图像变形。综合二者的优点,提出一种旋转不变的图像全局特征描述方法——梯度-径向夹角金字塔直方图(GRAPH),并将该特征应用在异源图像匹配中。同时重点介绍梯度-径向夹角金字塔直方图的计算方法,在得到图像的梯度-径向夹角金字塔直方图后,对基准图不同窗口的特征向量与实时图的特征向量进行比较,定义距离最近者为实时图在基准图中的最佳匹配。

2 梯度-径向夹角金字塔直方图

建立梯度-径向夹角金字塔直方图分为下面五个步骤:选取有效区域;计算径向矢量(radius direction vector,RDV);计算归一化梯度矢量(normalized gradient vector,NGV);计算梯度-径向夹角(gradient radius angle,GRA);用金字塔直方图(pyramid histogram,PH)统计有效区域内梯度-径向夹角的分布情况。

2.1 选取有效区域

为使图像特征描述具有旋转不变性,首先需要选取旋转不变区域作为计算特征描述的有效区域。在所有形状中,只有圆形能够满足旋转不变的性质,因此将特征描述的定义域设定为圆形。不失一般性,可以将图像中心看作图像旋转的轴心,则取以图像中心点为圆心的最大内接圆作为有效区域。如图1,白色圆形区域为有效区域,图像旋转前后有效区域内部的像素能够一一对应,而其他形状如灰色矩形区域内的像素无法对应。定义有效区域内的像素为有效像素,下文中所有的计算都是针对有效像素进行,不再另加说明。

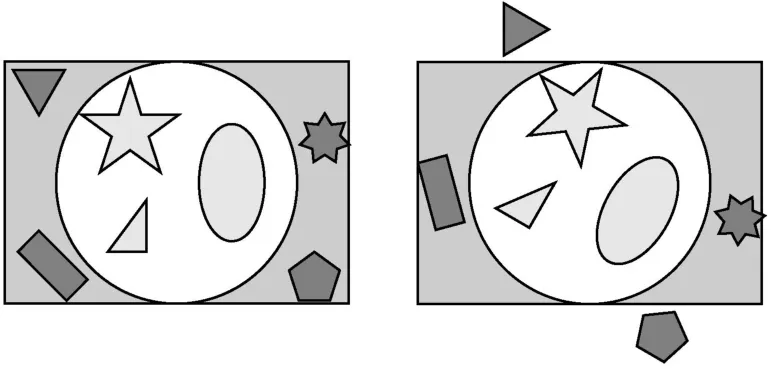
图1 有效区域选取示意图Fig.1 Select valid region

2.2 计算径向矢量

首先定义本文对矢量操作的标记符号。对于矢量v=a+bj,记矢量长度为矢量方向为∠v=acrtan(b/a)。对矢量旋转操作记为Rotate(v,θ),其中θ为顺时针旋转角度。下文中vr表示径向矢量,vd表示梯度矢量。

设图像有效区域的中心点为O(x0,y0),则对于任意有效像素A=I(x,y),定义该点的径向矢量为当图像旋转θ度后,A对应像素AR的径向矢量为

2.3 计算归一化梯度矢量

文献[10]中提出利用归一化梯度矢量进行匹配的方法。图像中一点 I(x,y)处的归一化梯度矢量定义为

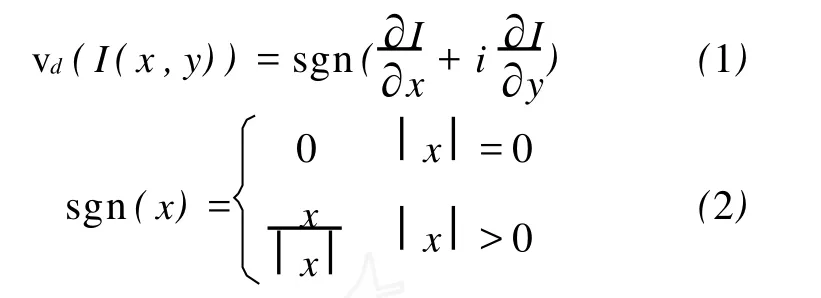
梯度矢量归一化操作本质上是去除梯度矢量的强度信息,只保留梯度矢量方向。文献[10]主要用归一化梯度矢量解决同源图像存在亮度变化时的匹配问题,并没有考虑异源图像灰度反转或存在密集噪声的问题,另外图像中存在梯度方向不稳定像素,如湖泊,其内部梯度很小但是通常不为零,则梯度方向一般仅受噪声影响,分布非常杂乱。将这类不稳定像素的归一化梯度矢量加入到图像匹配算法中,必将影响匹配的可靠性。

为了解决异源图像中灰度反转,即同名点的梯度方向可能相反的问题,一种直观的想法是将图像梯度由[0,2π)规定到[0,π),本文中将方向规定化操作放在计算梯度-径向夹角后进行,具体见2.4节公式(7)。

为了消除噪声影响,可以采用低通滤波。实际上,滤波操作还会增大梯度方向一致区域,利于图像匹配。

为了消除不稳定像素的影响,设定阈值 Th,舍弃梯度强度小于阈值的像素点。为了使阈值适用于不同类型图像,先将图像进行滤波和灰度线性增强处理。在灰度线性增强中,去除图像灰度直方图中最亮和最暗的像素各1%,将剩余的灰度级线性拉伸到[0,255]区间。梯度强度阈值 Th设为20,对于不同类型图像都得到较好结果。

2.4 计算梯度-径向夹角

图像旋转θ度后,I(x,y)对应的像素点为IR(x1,y1),其归一化梯度矢量也将旋转θ度。

定义vr与vd的夹角α为梯度-径向夹角。图像旋转θ度后,与A对应的像素AR的梯度-径向夹角为

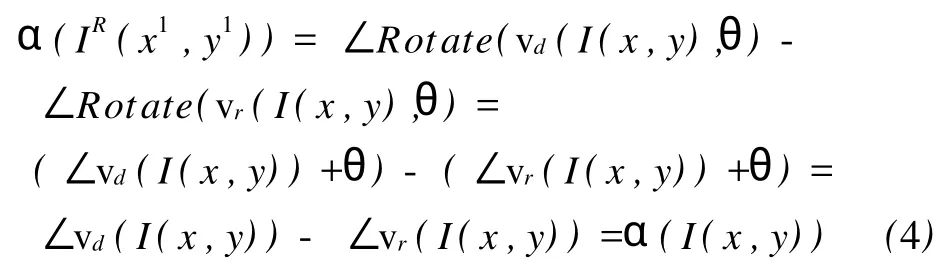
由上式可知,梯度-径向夹角不受图像旋转影响。已知归一化梯度矢量和径向矢量,则可通过反余弦函数计算梯度-径向夹角。

规定梯度矢量相位超前径向矢量相位时,梯度-径向夹角为正,将α量化到(-π,π),记为α2π,有如下计算公式,其中vdx、vdy分别为vd的实部和虚部,vry、vrx为 vr的实部和虚部。vdx×vry-vdy× vrx>0表示vd相位超前vr,vdx×vry-vdy×vrx<0表示vd相位滞后vr。

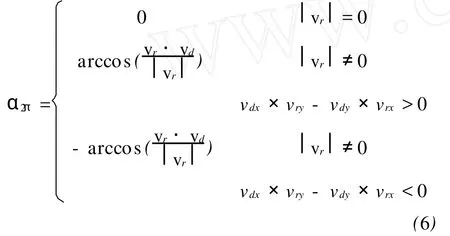
为了适应异源图像中梯度反向的情况,需将梯度-径向夹角量化到[0,π)。

需要特别说明,任意一点的径向矢量只与该点在窗口中的几何位置有关,故可以预先将窗口内每一点的归一化径向矢量制成二维查找表。在对基准图进行匹配搜索时,每个窗口只需查表就可确定其中每点的归一化径向矢量。图像匹配时,同样可以预先将反余弦函数制成查找表,通过查表加快算法速度。

2.5 圆形金字塔直方图

图像旋转后,由于对应点的空间坐标发生改变,无法直接比较对应像素的梯度-径向夹角。一种合理的方法是采用直方图表示图像的区域统计特征。建立梯度-径向夹角的直方图,则该直方图具有旋转不变特性。由公式(6)、(7)将夹角量化到[0,π)区间。本文中将角度空间划分12个区间,每个区间对应直方图一个栅格,则可以用12维向量表示直方图。

实际应用时,仅用12维向量表示一幅图像,则向量的分辨能力有限,无法实现可靠匹配。文献[13]在研究图像分类时,提出一种梯度方向的金字塔直方图特征,能够通过金字塔层数的改变调整对图像的表示能力。为了增加向量维数,提高特征的表示能力,同时保证特征描述的旋转不变性,本文采用一种圆形金字塔分层方法。图2是3层圆环金字塔示意图,其中L1层每个区域面积为L0层区域面积的一半,L2层每个区域面积为L1层区域面积的一半,依此类推。分别在L0、L1、L2层每个子区计算梯度-径向夹角直方图,由于不同层上的区域直方图统计的区域面积(有效像素)不同,用直方图向量除以该统计区域面积得到归一化直方图(为了计算时可以用整数表示直方图向量,再乘上L0层区域面积)。将全部归一化直方图向量首尾拼接,得到圆环区域金字塔直方图。图3为5层圆形金字塔梯度-径向夹角直方图特征,由372维向量表示。

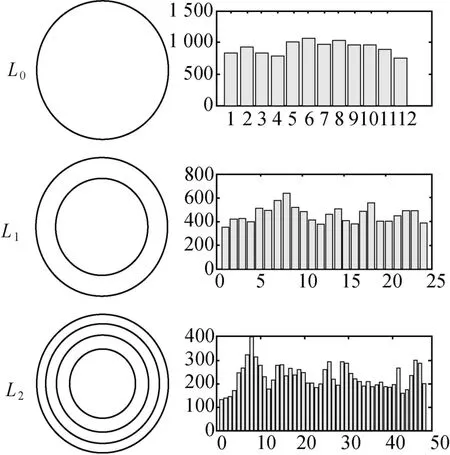
图2 圆形金字塔直方图Fig.2 Round pyramid histogram

图3 梯度-径向夹角金字塔直方图特征Fig.3 GRAPH descriptor

理论上,梯度-径向夹角金字塔直方图特征是一种真正的图像旋转不变稀疏特征描述,它不依赖于主方向的选取,比传统的方法有更强的适应性。梯度-径向夹角金字塔直方图特征能够实现图像灰度非线性变化,梯度方向反向等复杂条件下同源或异源图像间的匹配。

3 图像匹配算法实现

在图像匹配的许多应用中,只需要得到一幅图像中心点在另一幅图像中的对应位置,无需获得两幅图像的全部变换参数下精确配准。这种情况下,可以使用中心点匹配模型。中心点匹配模型中,有实时图 I1和基准图 I2,通常实时图场景完全包含在基准图场景中,匹配目的是要找出实时图中心在基准图中的对应位置。以图像中心为原点,用 TRT={x,y,θ}表示对基准图的平移-旋转变换(RT变换),IRT表示全体RT变换的集合,则图像匹配的目的就是寻找使某种条件达到极值的 TRTm。即

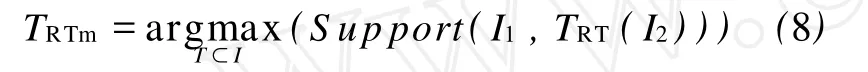
S upport(I1,TRT(I2))为对基准图做 RT变换 TRT时,对匹配的一种支持度。

如果能够找到一种旋转不变的图像描述D,使得S upport(D(I1),D(TRT(I2)))=S upport (D(I1),D(TT(I2))),其中 TT={x,y}表示对基准图的平移变换,则只需进行平移空间的搜索匹配,就能够得到最佳匹配位置。梯度-径向夹角金字塔直方图正是这样一种旋转不变图像描述。对于图像 I,其梯度-径向夹角金字塔直方图特征D(I)是一维向量。则可以设定 S upport(D(I1), D(TT(I2)))=-Dis(D(I1),D(TT(I2))),其中Dis(·)是向量间的χ2距离[14]。对于向量 va= {ai},vb={bi},有

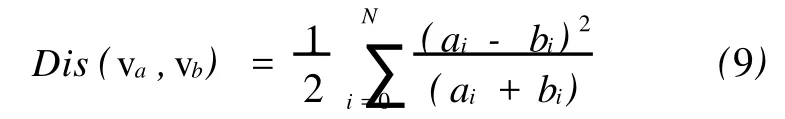
图4中给出基于梯度-径向夹角金字塔直方图的图像匹配算法,该算法适用于同源图像或者异源图像间的匹配。低通滤波和灰度线性增强是非常重要的两个预处理过程,试验中发现,对于SAR图像和可见光图像的匹配,如果不做这两步,将会影响匹配的效果。双查找表的加入大大提高了算法运算速度。整个匹配过程采用平移位置上搜索匹配的策略,搜索步长设为2像素。算法中的灰色区域表示该步骤可以在任务开始前离线处理和加载。因此,实时处理的步骤只有实时图的处理和直方图距离计算,大大减少了实时任务的计算压力。

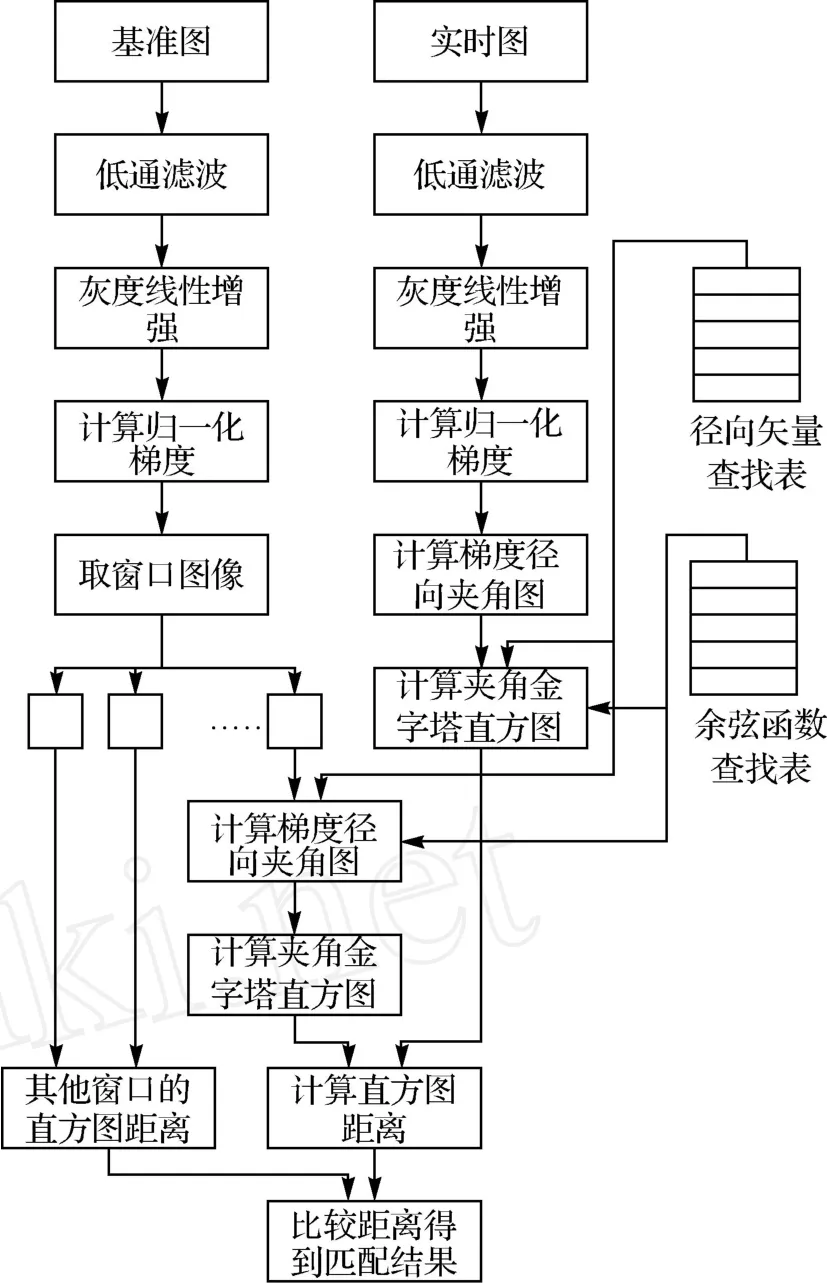
图4 图像匹配算法流程图Fig.4 Image matching algorithm flow chart

4 试验结果及分析

理论上,梯度-径向夹角金字塔直方图不受图像旋转和灰度级非线性变换的影响,为了验证这两个性质,下面用仿真图测试梯度-径向夹角金字塔直方图特征的抗旋转和灰度变化性能。图5中,第一行是输入图像和对应的梯度-径向夹角金字塔直方图特征。第二行是对输入图像旋转并作非线性灰度级变换和对应的梯度-径向夹角金字塔直方图特征。图中两个直方图相似度很高,通过计算直方图距离,发现它们之间存在细微差别。存在差别的主要原因是计算梯度时采用了3×3方形窗口,在图像旋转时,对应像素点的梯度矢量除旋转外还会存在由于方形窗口引入的误差,考虑到此差异很小,几乎不会对匹配造成影响,因此并没有采用更复杂的方法,如大尺度圆形窗口来消除它。图5中的试验说明梯度-径向夹角金字塔直方图特征能够克服图像灰度级非线性变换和图像旋转的影响。

图5 图像旋转和灰度级变换下的梯度-径向夹角金字塔直方图特征Fig.5 GRAPH feature after image rotation and grey level transform

为了测试梯度-径向夹角金字塔直方图特征对不同图像的表达力和分辨能力,对多幅卫星图像计算特征进行描述。采用χ2距离计算不同图像的梯度-径向夹角金字塔直方图特征间的差异程度,见表1,表内数值为向量距离,无量纲。试验说明,对于任意两幅不相关的图像,它们的直方图距离比较大,对于任意选择的7幅图像,直方图距离最小的为6 782。

对一幅卫星图像及其旋转30°和60°后的图像计算梯度-径向夹角金字塔直方图特征描述如图6。采用χ2距离计算得到直方图间距离如表2,其中最大的距离为648。与表1中的距离相比较,图像旋转产生的向量距离小一个量级以上。

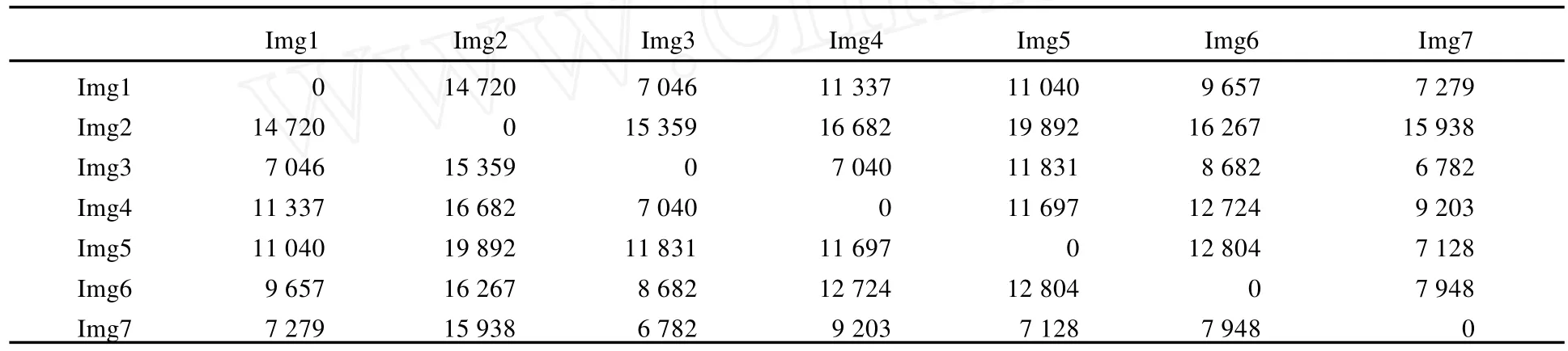
表1 不同场景图像的直方图特征距离Tab.1 Distances of different GRAPHfeature

图6 图像旋转不同角度的梯度-径向夹角金字塔直方图特征描述Fig.6 GRAPH feature descriptor respected to different rotate angles

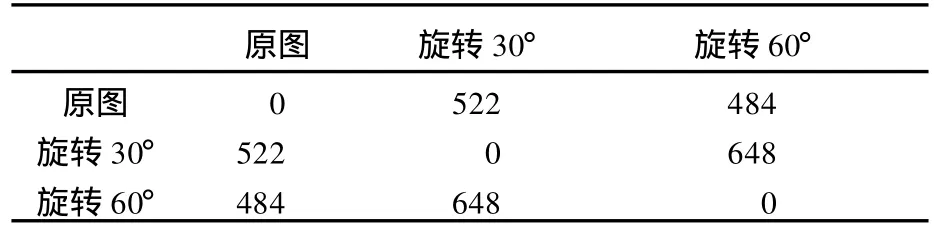
表2 图像旋转不同角度的梯度-径向夹角金字塔直方图特征距离Tab.2 Distances of different GRAPHfeatures respected to different rotate angles

基于梯度-径向夹角金字塔直方图特征进行图像匹配,首先测试匹配算法对同源图像的效果。基准图为一幅遥感照片,实时图是从基准图中选取的一小块区域,并进行了角度旋转。匹配结果如图7(a),实时图和基准图间只有平移和旋转变化,白色圆环的中心对应实时图中心在基准图中的匹配位置。图7(b)是过匹配点沿 x轴方向各窗口与实时图直方图相似性(距离倒数)曲线。匹配真值为(406,241),梯度-径向夹角直方图特征匹配结果为(406,240)。图7的试验验证了本文方法原理上的正确性,即对同源图像能够得到正确结果。

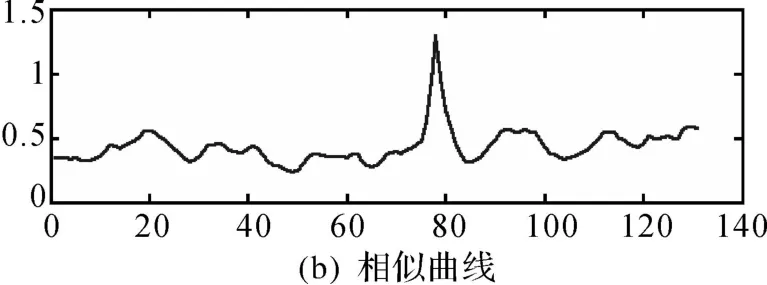
图7 旋转图像匹配Fig.7 Matching rotated images

为了测试梯度-径向夹角金字塔直方图特征对异源图像的匹配效果,选取美国Sandia国家实验室提供的SAR图像做实时图,Google Earth中的光学卫星图像做基准图,两图存在平移旋转变化,另外还有一定程度的图像畸变。为了考核匹配结果是否正确,手工选择多组同名特征点,用最小二乘方法得到最优匹配解作为匹配点的参考值。由于手选同名点的存在误差,故无法说明这两个结果哪个更真,但是只要结果接近,一般坐标差异在5个像素内,即可认为匹配结果可以接受,本方法只考核匹配正确性,并不考核匹配精度。采用梯度-径向夹角金字塔直方图特征匹配结果如图8(a)、9(a)。中心点匹配模型,图8(a)中匹配参考值为(363,220),本文方法匹配结果为(361,221),匹配结果与参考值距离约2个像素,故匹配结果正确。过匹配点沿 x轴方向各窗口与实时图直方图相似性曲线如图8(b),图8(c)、(d)分别为互信息和文献[8]方法匹配结果,匹配位置错误。图9(a)中匹配参考值为(116,330),本文方法匹配结果为(116,331),匹配结果正确。过匹配点沿 x轴方向各窗口与实时图直方图相似性曲线如图9(b),图9(c)、(d)分别为互信息和文献[8]方法匹配结果,匹配位置错误。

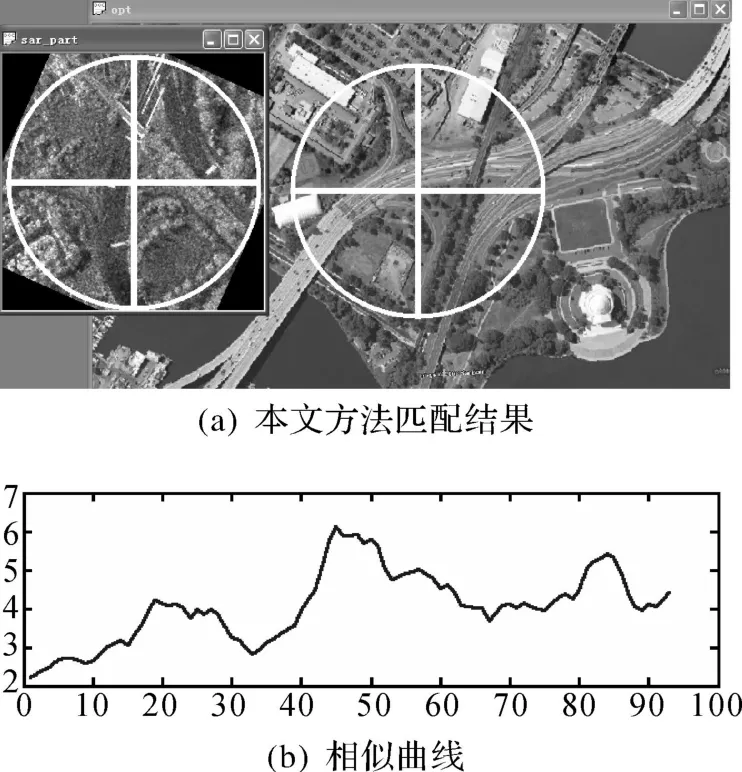
图8 异源图像匹配Fig.8 Matching multi-sensor images

图8、图9说明本文方法能够适用于异源图像的匹配,但是相似曲线主次峰比值较小,表明异源图像匹配结果可靠性没有同源图像匹配可靠性高。准备了一组待匹配图像,包括30对SAR图像和光学图像,SAR图像作为实时图,尺寸为300× 300像素,光学图像作为基准图,尺寸为600×600像素。分别对其中的SAR图像旋转15°、30°、45°得到另外三组待匹配图像。将本文方法与互信息及文献[8]方法进行了对比。本文方法将基准图直方图计算作为离线处理,不计入计算时间。互信息方法和文献[8]方法分别进行平移搜索和平移加旋转搜索,其中旋转搜索步长为10°。匹配成功率为成功匹配图像数比总的图像数。三种方法的匹配成功率和计算时间见表3。在图像只存在平移变换时,文献[8]方法只进行平移搜索时的成功率最高,本文方法次之,而文献[8]方法进行平移加旋转搜索时,其成功率大幅降低,低于本文方法。对旋转15°、30°、45°的图像进行匹配时,本文方法成功率远高于互信息方法和文献[8]方法。实时计算时间上本文方法远低于了互信息方法和文献[8]方法,降低了2个数量级以上。这是因为本文方法无需旋转搜索,且将基准图进行了离线计算,实时计算时只需获得实时图的梯度径向夹角直方图,并进行直方图比较操作。而另外两种方法对每个窗口计算时都同时需要实时图和对应基准图窗口内的全部像素信息,无法进行离线预处理。

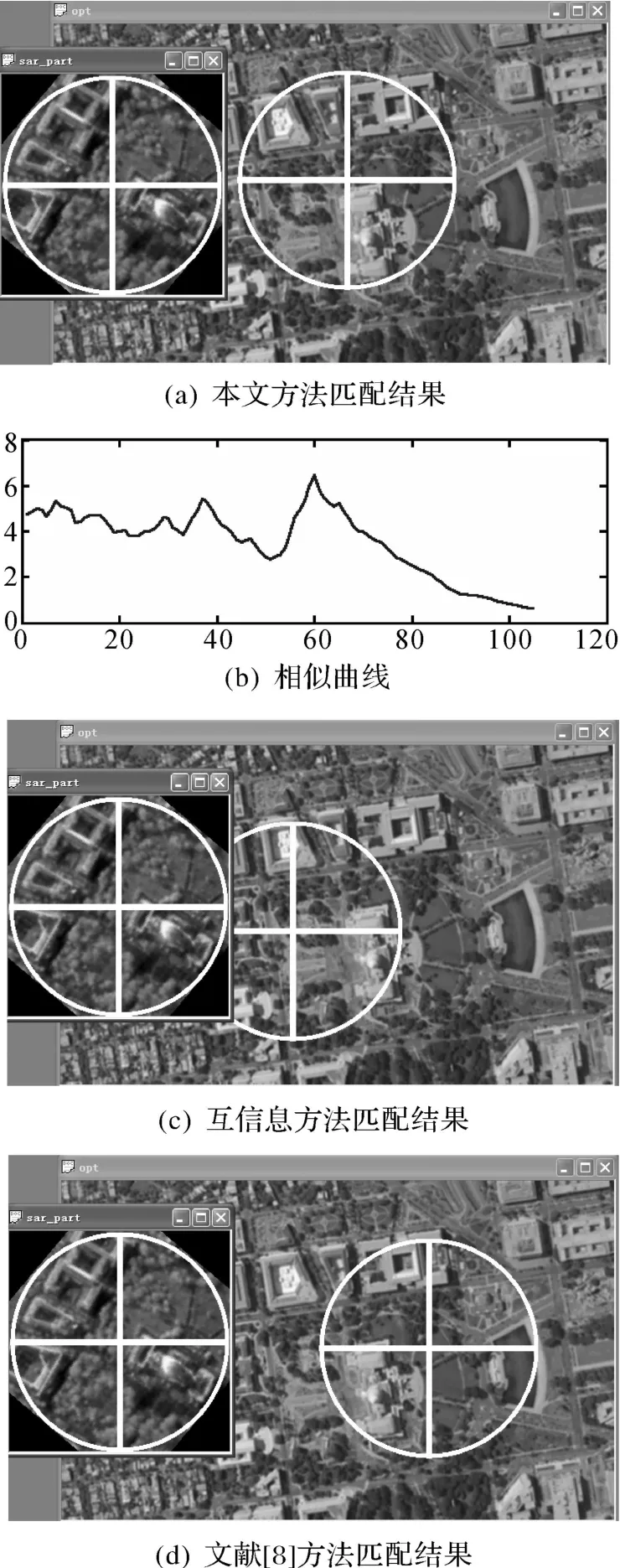
图9 异源图像匹配Fig.9 Matching multi-sensor images

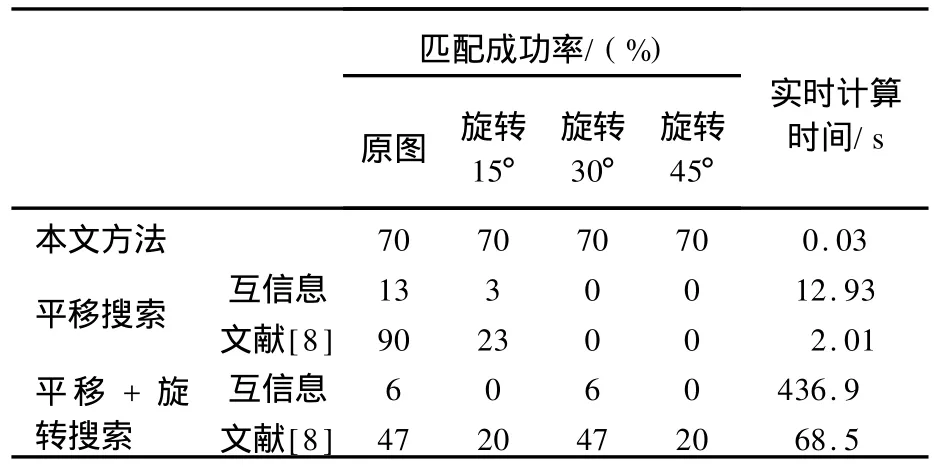
表3 不同匹配方法对比Tab.3 Comparison of different matching methods

上面试验中的异源图像之间存在复杂的几何形变,凭经验给出的匹配真值只能用以判断匹配正确与否,不能用来考核算法匹配精度。为此,制作仿真异源图对算法精度进行考核。首先选择内容丰富的光学卫星图像作为基准图。取基准图上的一部分区域,进行非线性灰度变换,加入斑点噪声并随机旋转一定角度,得到仿真实时图。通过对多组仿真图像的匹配试验得到匹配误差均值为0.9像素,误差方差为0.8。

5 结 论

本文提出了一种基于梯度-径向夹角金字塔直方图特征的旋转不变图像描述方法,并将它应用于任意旋转角度下的异源图像匹配。试验说明了该特征描述方法能够克服图像旋转和灰度变化。在存在图像旋转、平移和一定程度图像畸变的异源图像上进行了测试,结果表明该方法能够实现大部分异源图像间的正确匹配。另外本文方法在处理时间上大大优于各种常有的匹配方法。只利用梯度-径向夹角金字塔直方图特征进行匹配,尚无法解决图像存在较大尺度变化和形状畸变的情况下的匹配。下一步研究工作重点是提高匹配成功率,同时争取解决异源图像同时存在尺度和旋转变化时的匹配问题。

致谢:感谢美国Sandia国家实验室提供SAR图像,感谢Google提供光学卫星图像。

[1] CHEN Ying,YE Qin,ZHONG Zhiyong.Research on the Matching between Radar Image and Optical One Based on Wavelet[J].Acta Geodaetica etCartographica Sinica, 2000,29(3):245-249.(陈鹰,叶勤,钟智勇.基于小波变换的雷达与光学影像匹配算法研究[J].测绘学报,2000, 29(3):245-249.)

[2] BELONGIE S,MALIK J,PUZICHA J.Shape Matching and Object Recognition Using Shape Contexts[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002,24(4):509-522.

[3] VAN GOOL L,MOONS T,UNGUREANU D.Affine/ Photometric Invariants for Planar Intensity Patterns[C]∥Proceedings of the 4th European Conference on Computer Vision(ECCV′96).Cambridge:Springer,1996:642-651.

[4] LOWE D G.Distinctive Image Features from Scale-invariant Keypoints[J].International Journal of Computer Vision, 2004,60(2):91-110.

[5] KE Y,SU KTHANKAR R.PCA-SIFT:a More Distinctive Representation for Local Image Descriptors[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR′04).Washington: IEEE Computer Society,2004:506-513.

[6] BA Y H,TU YTELAARS T,VAN GOOL L.SURF: Speeded Up Robust Features[C]∥Proceedings of the 9th European Conference on Computer Vision(ECCV′06). Graz:Springer,2006:404-417.

[7] MIKOLAJCZYK K,SCHMID C.A Performance Evaluation of Local Descriptors[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR′03).Madison:IEEE Computer Society, 2003:257-263.

[8] ZHANG Shaoming,CHEN Yingying,LIN Yi.A Robust Matching Algorithm for SAR Image with Multiple Subareas[J].Acta Geodaetica et Cartographica Sinica,2007, 36(4):406-413.(张绍明,陈映鹰,林怡.用于末制导的SAR图像多子区实时匹配算法[J].测绘学报,2007,36 (4):406-413.)

[9] YU Qifeng,SHANG Yang.Videometrics:Principles and Researches[M].Beijing:Science Press,2009:96-102.(于起峰,尚阳.摄影测量学原理与应用研究 [M].北京:科学出版社,2009:96-102.)

[10] FITCH A J,KADYROV A,CHRISTMAS W J,et al. Orientation Correlation[EB/OL].[2010-01-10].http:∥citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1. 64.5662&rep=rep1&type=pdf.

[11] MAES F,COLLIGNON A,VANDERMEULEN D,et al.Multimodality Image Registration by Maximization of Mutual Information[J].IEEE Transactions on Medical Imaging,1997,16(2):187-198.

[12] LAMPERT C H,BLASCH KO M B,HOFMANN T.Beyond SlidingWindows:ObjectLocalizationby Efficient Subwindow Search[C]∥Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition(CVPR′08).Los Alamitos:IEEE Computer Society,2008:1-8.

[13] BOSCH A,ZISSERMAN A,MUNOZ X.Representing Shape with a Spatial Pyramid Kernel[C]∥Proceedings of the 6th ACM International Conference on Image and Video Retrieval(CIVR′07).Amsterdam:[s.n.],2007: 401-408.

[14] MARTIN D,FOWL KES C,MAL IK J.Learning to Detect Natural Image Boundaries Using Local Brightness, Color and Texture Cues[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2004,26(5): 530-549.

Matching Multi-sensor Images Based on Gradient Radius Angle Pyramid Histogram

LI Zhuang,LEI Zhihui,YU Qifeng
College of Aerospace and Material Engineering,National University of Defense Technology,Changsha 410073,China

A novel image feature named gradient radius angle pyramid histogram(GRAPH)is proposed.The GRAPH feature is invariable to nonlinear transform of grey level and image rotation,and is robust to noise.Based on GRAPH feature,we get a robust and fast image matching algorithm that can match rotated and shifted multi-sensor images.SAR images and optical images are used to test this matching method.The results show that the new matching algorithm has higher success rate than traditional method.As the reference image can be processed offline,the processing time is less then one in a thousand of the traditional used time.

multi-sensor image;image matching;rotate-invariant;gradient vector;radial direction vector; pyramid histogram

LI Zhuang(1982—),male,PhD candidate,majors in image registration and target recognition.

1001-1595(2011)03-0318-08

TP391

A

国家863计划(2007AA12Z121)

(责任编辑:雷秀丽)

2010-02-24

2010-07-31

李壮(1982—),男,博士生,主要研究方向为图像匹配和目标识别。

E-mail:lizhuang2007@hotmail.com