基于代数结构的地形图制图模型
2011-12-25朱海红邱俊武于忠海
李 霖,朱海红,贺 彪,王 红,3,邱俊武,于忠海
1.武汉大学资源环境学院,湖北武汉430079;2.武汉大学地理信息系统教育部重点实验室,湖北武汉430079;3.湖北大学资源环境学院,湖北武汉430062
基于代数结构的地形图制图模型
李 霖1,2,朱海红1,2,贺 彪1,王 红1,3,邱俊武1,于忠海1
1.武汉大学资源环境学院,湖北武汉430079;2.武汉大学地理信息系统教育部重点实验室,湖北武汉430079;3.湖北大学资源环境学院,湖北武汉430062
根据地图表达的特点,将地理空间信息抽象表达为二元结构,即反映语义属性及空间位置属性的地理要素和要素间空间关系;利用代数结构形式,在地理空间数据库和地图中分别构建表达地理空间信息的地理要素空间和地图要素空间;地理要素空间中的空间关系是基于欧式空间原理建立的,而地图要素空间中的空间关系则是用视觉模型来刻画。据此,提出以地理要素为对象的从地理要素空间向地图要素空间转换的制图模型。通过定义符号单元同核变换将目前制图过程中的符号化过程从面向地理要素类层延展到面向地理要素实例层,克服统一符号化过程不能同时满足共性和特性要求的矛盾;定义的地理要素有效移位变换可使地图制图过程更加流畅,减少中间人工干预过程。
地理空间信息;制图模型;符号化;代数结构;地图制作
1 引 言
地理信息可视化被认为是一种空间认知行为,它有助于人们观察、研究客观存在或各种自然、社会现象的空间分布,发现以往不易找到的规律[1],因此,地图被认为是认识空间和地理信息最有效的方式之一,成为地理信息系统与人们的交流窗口[2]。几十年来 GIS的地理空间数据管理、查询、显示和分析功能取得了巨大进展,但忽视了对地理信息可视化的深入研究,绕过制图模型(过程)从数据库直接生产地图尝试的受挫,使人们清醒地认识到制图模型的重要性,简单的图形符号显示策略并不能替代地图制作过程。许多专家学者已认识到地理信息与其可视化的地图在数据表达原理上有所不同,提出了数字景观模型(digital landscape model,DLM)和数字制图模型(digital cartographic model,DCM)的概念[3-7]。GIS中的地理空间信息被认为是数字景观模型,而地图上的地理空间信息被认为是数字制图模型。从制图过程看,DLM是地图制图的数据源,DCM是GIS的输出产品。文献[8]分析地理空间数据与地图数据的差异,从信息模型的角度阐述现有 GIS体系不能直接用于地图制图的原因。因此,通过考察信息转换过程,分析这两种模型的差别,探讨从地理空间数据到地图数据的转换过程是数字地图制图领域中的一项关键技术。
现有许多关于制图模型的研究中,主要集中在数据层面,例如,如何将地理现象/实体抽象成计算机世界中的概念模型,进而转换成数据库的逻辑模型和数据结构[9-16]。由于 GIS技术的快速发展以及电子地图应用的普及,地图输出被当作是GIS中地理空间数据可视化的一种辅助产品[8],因而忽略了对高质量地图制图过程的研究,这主要表现在:GIS软件系统在地图设计(cartographic design)和地图表达(cartographic presentation)功能方面并不能满足地图产品生产的要求[17]。拓展GIS的制图功能被认为是 GIS软件功能发展的重要趋势[7,17]。因此,深入研究地图制图的过程模型对设计和开发具有专业化制图功能的软件具有重要的指导意义。
为弥补GIS软件在制图表达上的不足,ESRI公司已在其ArcGIS平台上增加了制图表达规则(presentation rule)和覆盖(override)的机制。表达规则规定符号关联的要素属性(类型)和所要达到的几何图形样式;覆盖则提供在要素类共同表达规则下,具体要素实例可以特殊处理和表达的机制。图1实例说明其工作原理。

图1 制图表达规则/覆盖机制[29]Fig.1 Example for applying presentation rule/ overrides[29]
表达规则/覆盖机制在 GIS技术体系框架下更多的是在数据库层面上改进以前的数据模型,为在制图共性表达中兼容个性表达提供了存储与管理方案。这种改进仍然面向数据模型,如何提高制图过程的自动化程度,仍有待研究。
图1(c)初步展现出对一般符号化过程改进后,在地图表达方面的优点,这说明制图过程的效率可以通过改进地图符号化方法得以提高,因此,深入探讨面向制图过程的模型对于数据库驱动的制图过程具有重要的理论和实际意义。本文将主要以地形图的制图过程为例,从地理空间信息(为与一般性“地理信息”概念作区分,下文中的“地理空间信息”概念特指“基础地理信息”)结构方式来考察 GIS中地理空间数据转换成地图数据的过程及其特征,以代数结构方式来分析地图制作过程的原理和技术,提出一种从基础地理空间数据生产地形图的制图过程模型。
2 地理空间信息的代数结构
2.1 地理空间信息的基本结构
尽管GIS和地图在使用功能上各有侧重,但正确反映地理现象的空间位置和分布规律是它们共同的目标和要求。从地理空间信息在 GIS和地图表达之间的转换过程看,GIS中表示的地理空间信息是地图制图的信息源,地图是GIS中地理空间信息的有效应用出口。基于 GIS的对象模型(object model),地理空间信息可以表达为地理要素和要素间的空间关系,其信息结构可以用二元组表示

式中,S为地理空间信息世界;G为地理要素域(如河流、道路、居民地等);R为要素间的空间关系。
在GIS中,地理要素的语义信息通过存储的地理要素属性数据来描述。地理要素间空间关系可以利用要素精确的位置信息通过欧式空间原理来刻画,例如拓扑关系都可以通过欧式空间在需要时计算出来,也可以在数据结构设计时设计显式存储的拓扑数据结构预先将拓扑关系存储起来,需要时直接查询这些拓扑数据。其空间关系可以用自然语言或图示的方式提供给访问者。
在地图中,地理要素的语义信息(∈G)和空间关系(R)必须用视觉可辨认的方式反映到读图者的大脑中,其空间关系不是通过欧式空间原理计算,而是通过所谓视觉认知方式在大脑中建立起来的。地形图制图规范和图示标准是按照这种视觉空间认知规律对地图表达提出的具体规定和要求,这种地理空间信息呈现必须是明确和断然的,而不是隐含和渐进的。这也是作为最终产品的地图与在信息系统支持下的地理空间信息可视化的重要差别。这进一步说明了地理空间数据与地图数据的不同点,地理空间数据必须通过制图转换才能成为地图数据[18]。
2.2 地理空间信息的代数空间
根据上述分析,GIS世界中的地理空间信息可以用具有代数结构形式的(数学)空间Ω来定义

式中,Ω为地理要素空间;U为描述空间关系的模型,它是基于欧式空间原理下空间关系R的计算模型。
相应的,地图世界中的地理空间信息的代数空间Φ可以定以为

式中,Φ为地图要素空间;C为地图世界中对应地理要素域G的地图要素域;Q是通过地图要素反映出地理要素空间关系R的空间关系;V是描述(刻画)空间关系Q的视觉模型。
3 视觉模型中的空间关系
由于人类视觉认知在空间计算能力的局限性,地理要素间的许多空间关系并不能被视觉模型察觉,比如距离关系、长度或角度相等关系等都不能确定被视觉模型计算或判断出来。比如两条长度相同的线段,如果不进行叠加比较,很难明确判定它们的长短,视觉认知心理学的典型试验(图2)说明了这一点。图2中两条水平线段一样长,在添加不同方向的箭头后,视觉上的长度就不一样。然而,当图形度量(长度或面积)差异比较大时,这种差异可以被视觉模型分辨出来的,但没有统一的阈值,还受背景图形、方向及排列影响。
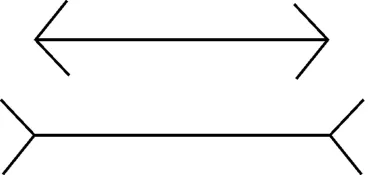
图2 两条等长线段的视错觉(缪勒-莱依尔错觉)Fig.2 Illusion of two segments with the same length (Muller-Lyer illusion)
因此,按视觉特性,地图上地理要素的空间关系一般主要表现为地图要素间的拓扑关系:相交、相切、相离。从地图制图过程的技术要求看,地理要素的空间位置基本保持不变,因此,仅仅考虑这些拓扑关系是有效和合理的。这些地图要素间的空间关系(拓扑关系),可以通过容限空间的概念在欧式空间中定义。
容限空间在视觉心理学研究具有重要的作用,揭示许多图形认知现象中的基本原理[19-20]。容限空间的概念定义为:集合 X中存在二元关系ξ,且关系ξ仅有反身性和对称性,称(X,ξ)为容限空间。基于此概念,定义点集 X的容限空间。
定义1:在欧氏空间中,点集 X的容限空间为ξX={y|d(y,x)≤ξ,x∈X},其中 d(y,x)表示两点x和y的欧氏距离,ξ为表示容限大小的数值。
据此,有下面地图要素空间上的拓扑关系(空间关系)。
定义2:两集合 X和Y具有拓扑相交,如果X∩Y≠∅。
定义3:两集合 X和Y具有拓扑相切,如果X∩Y=∅且ξX∩Y≠∅或 X∩ξY≠∅。
定义4:两集合 X和Y具有拓扑相离,如果ξX∩ξY=∅。
如果将上述集合 X定义为地理要素符号化后图形(即地图要素),ξ可以理解为地图上最小分辨率,则地图上地图要素间的拓扑关系可以通过欧氏空间的距离函数来计算。这是视觉模型中空间关系在欧式空间中的表达方式。
4 基于地理空间信息代数空间的制图模型
4.1 基本制图过程
根据上述地理空间信息的代数结构,通过对地理要素及其空间关系的转换,实现从地理空间数据(地理要素)到地图数据(地图要素)的转换,形成对地理要素的规范化地图表达。此转换过程可以定义为

因为要素间空间关系附着在要素上,因此,地理要素间空间关系的转换依赖于其地理要素的转换,即制图过程可以初步表达为

按此表达式,地图制图过程的理想情况是找到一个函数或过程 f,使其转换后的地理要素集f(G)满足地图要素空间关系Q的地图要素集C。
地图上地理要素的语义属性表达是用一套地图符号体系来实现,其空间属性的表达是通过在其原空间位置上对每个地理要素进行(地图)符号化后,其符号的位置体现出来。如果以标准地形图的制图要求为参照,地理要素的转换过程可以简单描述为依照地图规范要求的地图符号化过程(或转换函数)。从这种信息转换的角度看,地图符号化函数是地形图生产中提高自动化程度的关键,不同的地图符号化方法会对地形图生产过程产生不同的影响。
设地理要素域 G中的要素可以分成n个地理要素类,每个地理要素类对应一种地图表达(即地图符号)θ,n个子类型G1、G2、…、Gn对应n种符号表达θ1、θ2、…、θn,则

或对任意一个地理要素实例(相对于要素类)g∈Gi,通过符号化过程函数 fθi,得到相应的地图要素实例c∈Ci,即
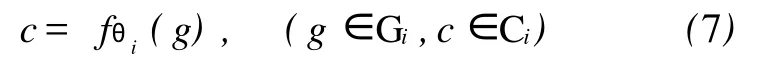
如果将每一种地图符号,都用这种过程化方式来实施对相应地理要素的地图符号绘制,那么,这样的制图转换(系统)需要设计 n个符号化函数,当n比较大时,对符号化函数的维护很不方便,特别当地图符号改变时,需要重新设计新的符号化函数。
如果将地理要素的符号化过程设计成基于数据(结构)表达的符号化运算,则可以提高制图系统维护的效率。利用二元运算的方式实施地图符号化的过程可以表示为c=g⊕θi,其中二元算子⊕是地图符号化算子,不同θi可以得到不同的符号化图案[21-23]。
此时,上述制图过程(或符号化函数)可以改成为二元函数
本文探讨的新媒体,是指利用网络和移动通信技术,通过互联网、无线通信网、卫星等渠道以及电脑、手机、数字电视等终端,向用户提供信息和服务的传播形态和媒体形态,它融合了报刊、广播、电视等传统大众传播媒体,能对所有有需求的大众同时提供个性化信息和服务,能实现传播者和接受者平等且多向的实时交流。伴随着信息技术的高速发展,以个人为中心的新媒体已经从边缘走向主流,逐步体现出与传统媒体不同的传播特点:一是信息传播的无边界性,可以跨越时间和空间的界限;二是传播方式的多向度性,由传统大众传播的点对多转变为多对多的网状结构模式;三是传播效果的消解性,发布者和受众间的身份边界消解、权威声音和所有者版权意识的消解。

式中,函数f没有限定其定义域的下标θi,表明将不同的符号θi带入制图过程f就得到不同符号图案的地图要素。
4.2 面向要素实例的地图符号化模型
设Θ为地图符号域,Θ中每一个元素(地图符号单元)θ定义为基本几何表达图形(即含有颜色、宽度等属性的基本几何图形如折线段、三角形、圆等)的有序集:θ=[p]。其中 p为基本几何表达图形。符号θ中元素的有序性反映出这些基本几何图形的绘制顺序,它可以处理一些图形关系,到达所要求的图案效果。每个地图符号单元θ都有自己的局部平面坐标系,根据其元素排列可以组成一个矩形图案,此矩形图案是一个基本符号单元,也用θ表示。矩形图案的Y轴方向范围称为符号单元宽,X轴方向范围称为符号单元长。
在地图符号域Θ中,尽管有些符号单元的图案不同,但在实施重复排列的线状要素符号化、或重复填充的面状要素符号化过程后,可以达到相同的地图符号表达效果(表达同样的地理类或属性)。如图3,两种铁路符号单元,符号化后表达出同样语义的地图要素。

图3 不同符号单元得到同样的视觉效果Fig.3 Same visual pattern generated by different symbol cells
线状符号这种重复排列的表达方式,可以通过选择不同的符号单元实现面向地理要素实例层次(即要素个体,而非要素类)的符号化,即根据具体地理要素的几何特征,选择合适的符号单元使符号化后的地图要素符合制图规范。例如图1中的(c)和(d),通过调整虚线符号的起点,可以避免符号虚部落在线段端点处和大的拐弯处。
为了进一步阐明这些符号单元的关系,给出符号单元柱面核和符号单元同核映射的概念。
定义5:将符号单元(或矩形图案)θ贴于高等于符号单元宽,周长等于符号单元长的圆柱面上,形成一个环状图案,称此圆柱面上的图案为符号单元柱面核(简称符号核或柱面核),记为π(θ)。
定义 6:Θ中的一种变换υ,使π(θ)= π(v(θ)),υ为符号单元同核变换(保核变换),简称同核变换。
同核变换υ使变换后的符号单元υ(θ)与原符号单元θ具有相同的符号核。根据符号单元θ的柱面核π(θ),可以在Θ构成一个符号单元的等价类Θ/θ:任何θ′∈Θ,使得π(θ′)=π(θ)。根据等价类Θ/θ,变换υ在集合Θ/θ上构成一个等价同核变换{υθ},即任何变换υ∈{υθ}使υ(θ)∈Θ/θ。
面状地理要素符号化的重复填充方式,是将符号单元在平面坐标系的 X和Y方向同时进行。类似地,也可得到符号柱面核和同核变换,在此,不加区分地统一用符号柱面核(符号核)π(θ)和等价变换υθ来描述符号单元间关系和变换。
据此,上述制图过程可以变为

根据符号等价变换集{υθ}为每一个地理要素元素 g(实例)构造出C中的等价集:C/(υθ,g)= {c|c=f(g,υ(θ)),υ∈{υθ}}。
根据地图符号设计及表达的原理,任何C/(υθ,g)中的元素,都正确反映地理要素的语义(非空间)属性,它们在地图图面的图案相同,但地图要素的图案表达中,同一空间位置上的局部图形有所不同。正是利用这些差异,可以使某个地图要素c在地图图面上表达的效果比其他地图要素c′更符合制图规范(例如让虚线符号不在虚部相交和虚部转折)。
4.3 基于地理要素转换的制图模型
上述 f(g,υ(θ))中υ(θ)的变换并不改变要素的几何位置,符号化后地图要素占据着一定的物理空间,从而会使原来不重叠的地理要素在空间上发生重叠,为此,需要调整(改变)原始地理要素的几何位置,从而保证符号化后地图要素间表现出的空间关系能正确地反映出原地理要素间的空间关系。
设μ是G中的连续位移变换,具有拓扑同伦性(homotopical mapping)。对地理要素 g(空间点集)可以实施不同的位移变换μ,使其空间位置(和形态)发生一系列改变。关于地图上要素几何图形位移计算方法已有许多成果[24-26],因受篇幅限制,不在此赘述。
对 g进行一组位移变换{μi}可以得到一系列新的元素{μi(g)},其中一定存在位置改变幅度最小的位移变换,用μmin表示。
定义7:设 gi,gj∈G,gi∩gj=∅,在 C中相应的符号单元分别为θi和θj(可能有π(θi)= π(θj)),并且 f(gi,υ(θi))∩f(gj,υ(θj)≠∅,G中对gi的位移变换μg称为对gi的有效位移变换,如果μ满足下列条件:
(1)如果ξgi∩gj≠∅∨gi∩ξgj≠∅,则
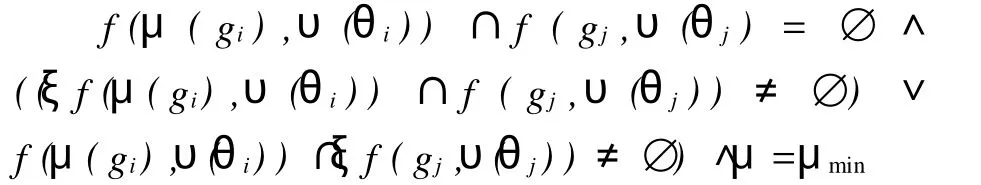
(2)其他情况下

同理,为避免对一个地理要素的位移幅度过大,可以对两个地理要素 gi和 gj同时进行相对的位移变换,达到其符号图形不重叠的制图要求。
当符号化的地图图形产生视觉冲突时,通过对地理要素进行有效位移变换,使之符号化后的地图要素仍能保持正确的空间关系。
因此,最终的制图过程变成为

从定义7条件式看,如果符号单元尺寸确定,根据两地理要素 gi和gj的几何位置完全可以确定出对gi和/或 gj的位移μ(gi)和μ(gj),因此,此模型为解决空间关系的视觉冲突,维护地理要素空间关系在两个代数空间的一致性提供可行有效的计算方法。
5 结 论
长期以来随着电子地图和多媒体呈现技术的发展,忽视对高质量地图产品生产过程及方法的研究,使得目前地图生成成为地理空间信息深入应用的一个瓶颈。利用地理空间数据库进行地图生产被认为是地理空间信息工程应用的关键技术[7,11-12,17],基于制图过程的制图模型是这项关键技术的理论基础和开发指南。
本文以地形图制图过程为参考,通过分析地理空间信息在制图过程中的表示形式,应用代数结构方式建立两个空间中的代数结构Ω=(G, R,U)和Φ=(C,Q,V),提出基于此代数结构的制图模型。此模型不仅指出提高制图过程自动化程度的关键因素,还在原理上揭示制图过程中地理空间信息转换的机理,为数据库驱动的制图系统功能设计提供良好的理论基础。然而,地图上有些要素符号图形间的相交和相接关系高度依赖于所设计的符号图形本身,因此,如何建立和处理这些图形关系模型是今后研究的重要方向。此外,对本模型的应用实例开发也是本研究后期工作的一项重要任务。
[1] GAO Jun.Visualization of Geo-spatial Data[J].Engineering of Surveying and Mapping,2003,9(3):1-7.(高俊.地理空间数据的可视化[J].测绘工程,2000,9(3):1-7.)
[2] WAN G Jiayao.Achievements and Tasks in Modern Cartography and Geo-information Engineering[J].Journal of Institute of Surveying and Mapping,2004,21(4):235-240.(王家耀.现代地图科学与地理信息工程科学技术的成就和任务[J].测绘学院学报,2004,21(4):235-240.)
[3] BRASSEL K E,WEIBEL R.A Review and Conceptual Framework of Automated Map Generalization[J].International Journal of Geographical Information Systems,1988, 2(3):229-244.
[4] GRUNREICH D,POWITZ B,SCHMIDT C.Research and Development in Computer-assisted Generalization of Topographic Information at the Institute of Cartography, Hanover University[C]∥ Proceedings ofthe Third European Conference on Geographical Information Systems.Utrecht:EGIS,1992:532-541.
[5] MULLER W,SEYFERT E.Quality Assurance for 2.5D Building Data of the ATKIS DLM 25/2[C]∥ ISPRS Commission IV Symposium:GIS—Between Visions and Applications.Stuttgart:ISPRS,1998:411-416.
[6] WEIBEL R,DUTTON G.Generalizing Spatial Data and Dealing with Multiple Representations[M].Cambridge: John Wiley&Sons Inc,1999:125-155.
[7] HARDY P,BRIAT M O,EICHER C,et al.Databasedriven Cartography from a Gigital Landscape Model,with Multiple Representation and Human Overrides[C]∥ICA Workshop on‘Generalisation and Multiple Representation’.Leicester:ICA,2004:20-21.
[8] AILEEN B,CHARLIE F,BARBARA B,et al.An Information Model for Maps:Towards Cartographic Production from GIS Databases[C/OL].[2010-02-11].http:∥www. cartogis.org/autocartoarchive/autocartopapers-2005.
[9] PEUQUET D J.A Conceptual Framework and Comparison of Spatial Data Models[J].Cartographica,1984,21(4): 66-113.
[10] CHRIST F.Cartographic Models for Digital Topographic Maps[C]∥Proceedings of AutoCarto,Hardware,Data Capture and Management Techniques.London:AutoCarto, 1986:247-256.
[11] BURROUGH P A.Are GIS Data Structures Too Simple Minded[J].Computers and Geosciences,1992,18(4): 395-400.
[12] GOODCHILD M F.Geographical Data Modeling[J]. Computers and Geosciences,1992,18(4):401-408.
[13] HADZILACOS T,TRYFONA N.Logical Data Modeling for Geographical Applications[J].International Journal of GeographicalInformation Systems,1996,10(2): 179-203.
[14] FRYE C,EICHER C.Modeling Active Database-driven Cartography within GIS Databases[C]∥Proceedings of the 21st International Cartographic Conference: Cartographic Renaissance.Durban:ICA,2003.
[15] STOTER J E,MORALES J M,LEMMENS R L G,et al.A Data Model for Multi-scale Topographic Data[C]∥Headway in Spatial Data Handling:13th International Symposium on Spatial Data Handling.Berlin:Springer, 2008:233-255.
[16] JAN H,HAROLD M,ANTONY C,et al.An Initial Formal Model for Spatial Data Infrastructures[J].International Journal ofGeographicalInformation Science, 2008,22(11-12):1295-1309.
[17] AILEEN B,HARDY P.Cartographic Software Capabilities and DataRequirements:CurrentStatus and a Look toward theFuture[J].Cartography and Geographic Information Science,2007,34(2):155-157.
[18] LI Lin,YIN Zhangcai,ZHU Haihong.Concept and Schema of Map-making Markup Language[J].Acta Geodaetica et Cartographica Sinica,,2007,36(1):108-111.(李霖,尹章才,朱海红.地图制图标记语言的概念与模式研究[J].测绘学报,2007,36(1):108-111.)
[19] CH EN Lin.Gestalt and Tolerance Space[J].Acta Psychologica Sinica,1984,17(3):32-39.(陈霖.格式塔和容限空间[J].心理学报,1984,17(3):32-39.)
[20] REDA KTSIYA K.Tolerance Space Theory and Some Applications[J].Acta Applicandae Mathematicae,1986, 5(2):137-167.
[21] LI Lin,XU Qingrong.Algebraic Operator Based Symbolization of Liner Features in CAC[J].Geomatics and Information Science of Wuhan University,1992(1):66-73.(李霖,徐庆荣.机助制图中线状符号的代数运算[J].武汉测绘科技大学学报,1992(1):66-73.)
[22] MEI Yang,LI Lin.Design and Research of Semi-line and Semi-area Map Symbol[J].Science of Surveying and Mapping.2006,31(1):115-116.(梅洋,李霖.地图中半线半面符号的设计与研究[J].测绘科学,2006,31(1): 115-116.)
[23] YANG Yong,LI Lin,WANG Hong,et al.Cartographic System Based on National Fundamental Geographic Data [J].Geomatics and Information Science of Wuhan University,2008,33(3):261-264.(杨勇,李霖,王红,等.基于国家基础地理信息数据的地图制图系统[J].武汉大学学报:信息科学版,2008,33(3):261-264.)
[24] RUAS A.A Method for Building Displacement in Automated Map Generalization[J].International Journal of Geographic Information Science,1998,12(8):789-803.
[25] BADER M.Energy Minimization Methods for Feature Displacement in Map generalization[D].Zurich:University of Zurich,2001.
[26] WU Fang,HOU Xuan,QIAN Haizhong,et al.A Model forRoadNetworkDisplacementinAutomatedMap Generalization[J].Acta Geodaetica etCartographica Sinica,2005,34(3),262-268.(武芳,侯璇,钱海忠,等.自动制图综合中的线目标位移模型[J].测绘学报,2005, 34(3),262-268.)
[27] PUNT E M,JENSEN R,HAEDY P,et al.Cartography: From Drawing to Database (Technology Facilitates Traditional Styles)[C/OL].[2010-02-10].http:∥www. pghardy.net/paul/papers.
[28] FRYE C.A Product-driven Approach to Designing a Multi-purpose,Multi-scale GIS Base Map Database that Supports High-quality Mapping[C/OL].[2010-02-12]. http:∥www.cartogis.org/autocartoarchive/autocartopapers-2006.
[29] NEUFFER D,SCHNEIDER S,HARDY P,et al.Database Driven Cartography—The‘swisstopo’Example.[C/OL]. [2010-01-29].http:∥www.pghardy.net/paul/papers/ 2006_gicon_vienna_esri.pdf.
Cartographic Model for Topographic Maps Based on Algebraic Structure
LILin1,2,ZHU Haihong1,2,HE Biao1,WANG Hong1,3,QIU J unwu1,Y U Zhonghai1
1.School of Resources and Environmental Science,Wuhan University,Wuhan 430079,China;2.Key Laboratory of GIS of Ministry of Education,Wuhan University,Wuhan 430079,China;3.Faculty of Resources and Environment Science,Hubei University,Wuhan 430062,China
A cartographic model being put forward characterizes the process of map-making by a transformation from geographical space to map space based on an algebra structure,and provides with a theoretical foundation and operational guideline for this merging technology.According to cartographic presentations of geo-spatial data in topographic maps,geo-spatial information is abstracted into two elements:geo-features and spatial relationships between the features,and further structured in form of algebra into two algebraic spaces:geo-feature space in a geo-databases world and map-feature space in a map world respectively.The spatial relationships in geofeature space are modeled by Euclidean space and the spatial relationships in map-feature space are calibrated by the visual cognitive mechanism.The cartographic model is built up by transforming geo-features into map-features which is restrained by the consistent spatial relationships in the two spaces.By defining an equivalent-kernel transform among symbol cells,a map symbolization for feature classes is extended for feature instances,fitting cartographic representations being both specified and universalized.With defining the displacement transform for geo-features,the process of map-making proceeds more smoothly,reducing being intervened to a large extent.
geo-spatial information;cartographic model;symbolization;algebraic structure;map-making
LI Lin(1960—),male,PhD,professor, PhD supervisor,majors in digital cartography,geo-ontology model,geo-information visualization.
1001-1595(2011)03-0373-06
P283.7
A
国家自然科学基金(40871178);国家863计划(2008AA121601;2007AA12Z241;2007AA120501)
(责任编辑:宋启凡)
2010-02-24
2010-05-11
李霖 (1960—),男,博士,教授,博士生导师,主要从事数字地图制图、地理信息本体模型、地理信息可视化等方向的研究。
E-mail:lilin@whu.edu.cn
