基于半监督核模糊c-均值算法的北京一号小卫星多光谱图像分类

刘小芳,何彬彬,李小文

1.电子科技大学地表空间信息技术研究所,四川成都610054;2.四川理工学院计算机学院,四川自贡643000

基于半监督核模糊c-均值算法的北京一号小卫星多光谱图像分类

刘小芳1,2,何彬彬1,李小文1

1.电子科技大学地表空间信息技术研究所,四川成都610054;2.四川理工学院计算机学院,四川自贡643000

针对遥感图像数据大多不服从高斯分布以及遥感图像分类存在非线性、模糊性和标记数据少等问题,提出基于半监督核模糊c-均值算法的多光谱遥感图像分类方法。首先,把半监督学习理论和核理论同时引入模糊c-均值算法,形成半监督核模糊c-均值算法。然后,用该算法与k-均值算法、最大似然算法、多类支持向量、半监督核支持向量、模糊c-均值算法、核模糊c-均值算法和半监督模糊c-均值算法对IRIS数据和北京一号小卫星多光谱图像进行分类试验。最后,对其分类结果进行评价。结果表明,对比其他分类算法,半监督核模糊c-均值算法能显著提高分类精度。

遥感图像分类;半监督核模糊c-均值算法;北京一号小卫星;核理论;半监督学习

1 引 言

由于传统的无监督遥感图像分类方法是根据数据集潜在的相似性和合适的测度,对输入数据集进行聚类,这种方法有时得不到好的分类结果[1]。而监督分类需要大量的训练数据集来设计分类器,如果选择的训练数据集不足以估计分类的参数,得到的分类效果也不好[2]。基于上述问题,提出半监督核模糊c均值算法,并以北京一号小卫星多光谱图像为例进行分类试验验证。具体思路如下:①针对遥感数据存在大量的不确定性,采用模糊分类算法更能处理遥感数据的不确定性(模糊性)[3-4];②获取遥感图像对应地面上的大量标记(已知类别)数据困难,但并不是对地面的地物信息一无所知,获取少量的标记数据是可行的,把半监督学习理论引入FCM算法,利用标记过的数据来指导分类,可以提高分类效果,为了减少遥感图像分类对标记数据的要求,半监督分类方法是一种更有效的遥感图像分类方法;③遥感图像分类多数是非线性分类问题,把核理论引入FCM算法,使输入特征向量被隐式地映射到高维空间,原来在低维空间非线性不可分模式在高维空间变成线性可分。

2 模糊c-均值算法

FCM算法是一种自组织学习方法,通过优化目标函数得到每个数据到类中心的隶属度,从而决定数据的归属。设待分类的数据集为 Xn×q= [x1x2… xn]T⊂Rq,如果要将矩阵 X划分为c个类别,Bezdek定义的模糊c-均值算法[5-6]的一般描述为

满足

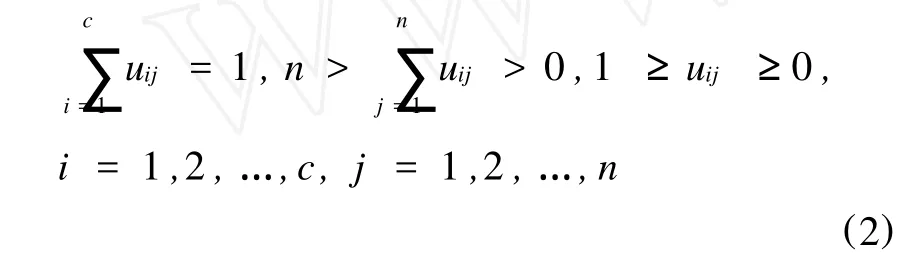
式中,Uc×n=[u1…uj…un]⊂Rc是隶属度矩阵(模糊划分矩阵),其中 uj=[u1j…uij…ucj]T;uij表示第j个数据xj属于第i个类别中心vi的隶属度; Vc×q=[v1…vi…vc]T⊂Rq是聚类中心矩阵,vi表示第i类的中心;m控制着隶属度矩阵在类间的模糊程度,m→1,隶属度矩阵趋向于硬划分,m→∞,逐渐软化隶属度矩阵,使划分变得越模糊,也可以根据试验确定参数 m,实际应用中一般取[2,2.5][7];J(X,U,V)是误差平方和目标函数; dij=‖vi-xj‖,i=1,2,…,c,j=1,2,…,n,这里dij选择 Euclid距离。

聚类准则是求得适当的模糊划分矩阵Uc×n= [uij]与聚类中心 Vc×q=[vi]使得目标函数J(X,U,V)达到极小值,根据拉格朗日乘数法求得uij、vi分别为

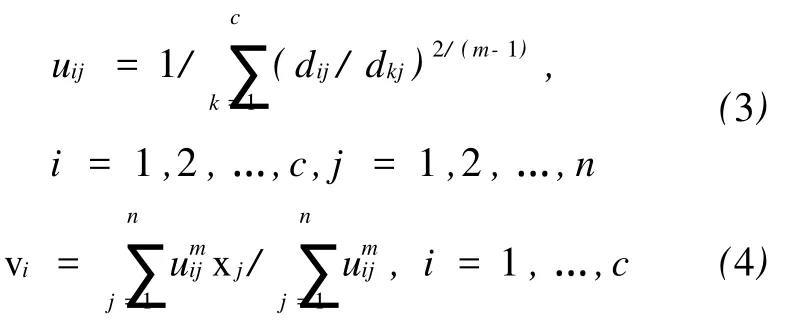
3 半监督核模糊c-均值算法

FCM算法是一种模糊模式识别方法,它是对传统聚类方法的扩展。但是,当数据之间存在交叠时,FCM算法不是很有效[8-10]。该算法是一种无监督算法,不能有效利用标记数据引导未标记数据的分类。因此,这里提出一种更有效的半监督核模糊c-均值(semi-supervised kernel FCM, SSKFCM)算法,它是把核理论和半监督学习理论同时引入FCM算法而形成的。

3.1 核模糊c-均值算法

把核理论引入FCM算法,形成核模糊c-均值(kernel fuzzy c-means,KFCM)算法。核的基本思想是通过构造新的特征向量将输入模式空间映射到高维特征空间,将原空间的非线性问题转化为高维特征空间的线性问题进行处理[11-12]。KFCM算法采取核理论修改FCM算法的目标函数,用式(5)的诱导核距离代替 FCM算法在式(1)中的Euclid距离。KFCM算法的目标函数如式(6)所示。

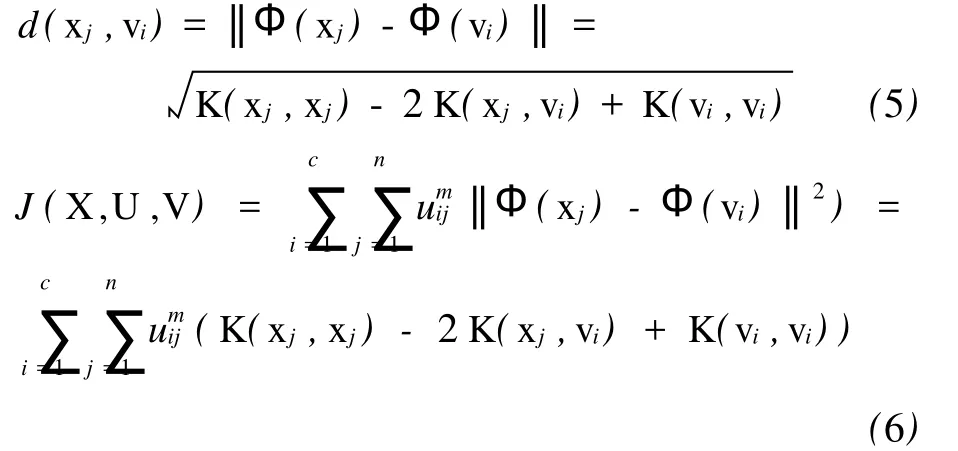
特别的,对径向基核函数 K(x,y)= exp(-‖x-y‖2/2σ2),当∀x∈X,有 K(x,x)= 1,式(6)的 KFCM算法的目标函数简化为式(7)。

式中

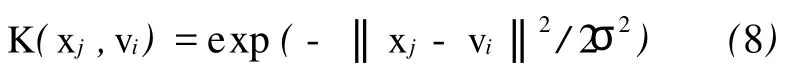
KFCM算法的最小化过程类似于 FCM算法。根据拉格朗日乘数法,为了求得适当U= [uij]、vi使目标函数J(X,U,V)达到极小值,即构造一个拉格朗日函数

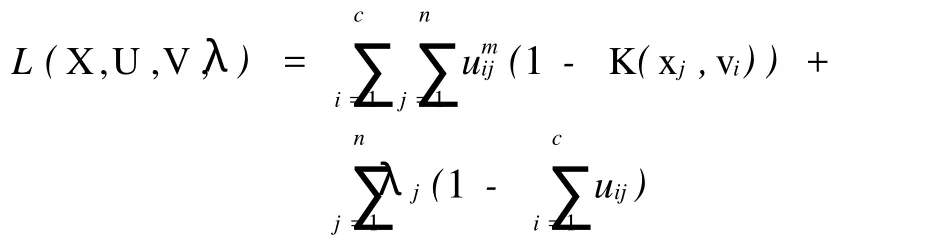
由∂L(X,U,V,λ)/∂uij=0,得

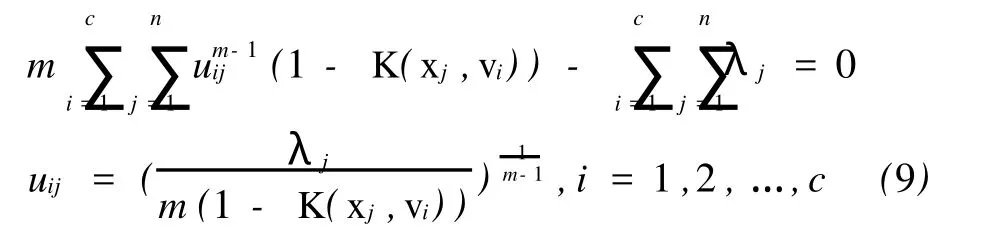
即

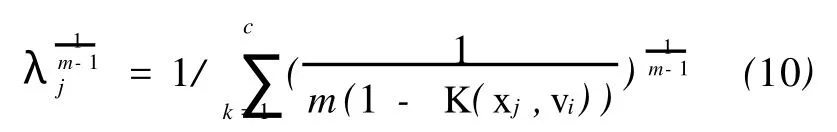
把式(10)代入式(9),得模糊划分矩阵U= [uij]为

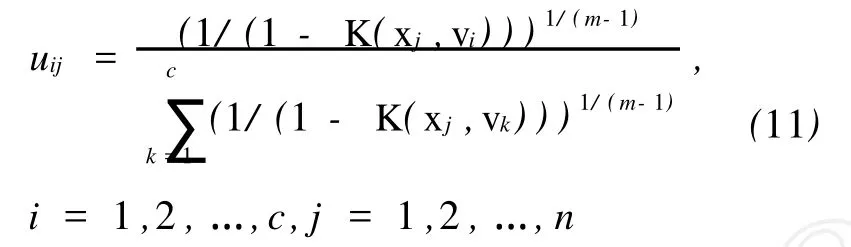
由∂L(X,U,V,λ)/∂vi=0,得

得聚类中心vi为

3.2 半监督核模糊c-均值算法

如果在分类前已知少量数据的类别,则可以将这些数据作为标记数据引入到 FCM算法和KFCM算法形成半监督模糊 c-均值 (semisupervised FCM,SSFCM)算法[13]和半监督核模糊c-均值(SSKFCM)算法。半监督学习方法是使用少量标记数据指导未标记数据的分类。

待分类的数据为 X=[XbXu],其中,Xb和Xu分别表示已标记和未标记数据,nb和nu分别是Xb和 Xu的个数。模糊划分矩阵U= [UbUu],其中,Ub是已标记数据 Xb的化分矩阵,取值按硬划分赋值。Uu是未标记数据Xu的模糊化分矩阵,在算法的迭代过程中,对SSFCM和SSKFCM算法,Uu分别按式(3)和式(11)进行更新。因此,初始化的模糊划分矩阵为U(0)= [Ub],迭代过程中的模糊化分矩阵为

3.3 SSKFCM算法的实现步骤

FCM、KFCM、SSFCM和SSKFCM算法的具体实现步骤相似,都是通过迭代原理实现,不同算法使用的计算公式不一样。以SSKFCM算法为例,算法的具体实现步骤如下:

(1)给定有部分标记数据的数据 X= [XbXu]。

(2)初始化c、m、迭代截止误差值ε、算法的最大迭代次数 Tmax。按式(2)的三个约束条件初始化模糊划分矩阵U(0)=[Ub]中的。用标记数据 Xb的各类的中心初始化聚类中心

(3)修改迭代次数,t=t+1。

(4)根据式(8)的径向基核函数,计算核函数矩阵 K(t)(xj,vi(t-1))。

(5)由U(t-1)=[UbUu(t-1)],根据式(12)计算聚类中心vi(t)。

(6)根据式(7),计算目标函数 J(t)(X, U(t-1),V(t-1)),判断算法在迭代过程的收敛性。

模糊划分矩阵U=[uij]包括了数据集 X的模糊分类结果,如果利用最大隶属度原则,数据Xj归属于最大隶属度这类,这个过程称为去模糊化,得到硬划分矩阵U。

4 试验仿真与结果分析

为了验证算法的有效性,试验数据选取UCI数据库的数据集 IRIS[14]和一个遥感图像数据。试验平台为pentium4 1.8 GHz处理器、2 G内存、Windows XP操作系统。算法用C和MATLAB混合编程实现。用IRIS数据作为理论验证数据,因为IRIS数据是国际公认的比较聚类方法效果好坏的典型数据之一。它包含了150个四维的3类数据,每类各50个样本点,数据特点为一类数据与其他类数据离得较远,另外两类数据离得较近,而且有部分数据交叠。遥感数据来源于北京一号小卫星32 m的多光谱(绿B1:520～620 nm、红B2:630～690 nm、近红外B3:760～900 nm)的遥感图像。该数据为经过几何校正的二级产品,成像时间为2007-09-14T 11:30:29—11:34:59,图像大小为1 390×1 500像素。分类特征分别为IRIS数据的4种属性和北京一号小卫星图像的3个波段。

试验进行了三方面的分类算法比较:①与传统的无监督分类的k均值(k-means,KM)算法和监督分类的极大似然(maximum likelihood,ML)算法[15]比较;②与FCM及其改进算法 KFCM、SSFCM的比较;③与利用核方法的多类支持向量机(multiclass support vector machines,MSVM)[16]和半监督支持向量机(semi-supervised support vector machines,S3VM)[17]的比较。

4.1 IRIS数据的试验结果

对数据集IRIS,每类取65%作为训练数据, 35%作为测试数据。对 ML、MSVM、S3VM、SSFCM和SSKFCM算法以训练数据作为监督数据。MSVM、S3VM、KFCM和SSKFCM算法的核函数取式(8)的径向基核函数,通过五重交叉验证,MSVM和S3VM算法的核参数σ=0.5、正则化参数C=1,S3VM算法的无标记数据的正则化参数C＊=1;KFCM和SSKFCM算法的核参数σ =0.9。MSVM和S3VM算法采用原模式的对偶模式,用序贯最小优化方法实现,并用一对多分解方法扩展到多类SVM。几种算法对IRIS数据的分类精度如表1所示。

表1 几种算法对IRIS数据的分类精度Tab.1 Classification accuracy of several algorithms for IRIS data set

对IRIS数据的分类结果表明,有足够训练数据的情况下,监督分类的ML和MSVM算法的分类效果好于其他算法,但半监督分类的S3VM和SSKFCM算法也显示了强的分类能力。

4.2 北京一号小卫星图像的试验仿真与结果分析

北京一号小卫星图像分类流程如图1所示。数据规格化处理选用数据标准化变换。评价指标以分类后的混淆矩阵为基础,计算用户精度、制图精度、总体分类精度和kappa系数。

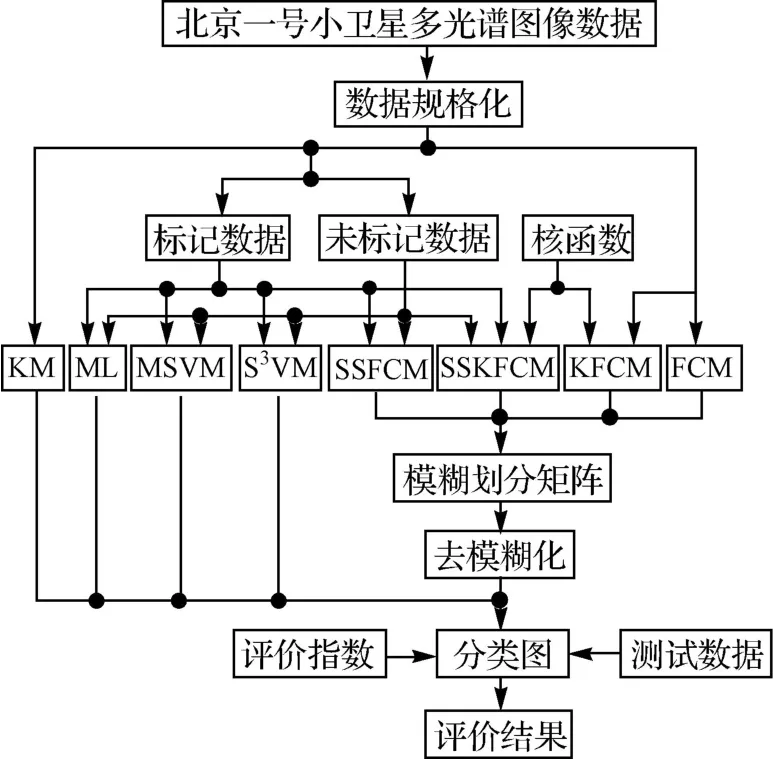
图1 几种算法的北京一号小卫星图像分类流程Fig.1 Flowchart of the classification for Beijing-1 micro-satellite image by several algorithms

4.2.1 试验结果

试验数据中主要包括水体、植被、雪、戈壁四类地物,并且有些地物之间波谱特征存在一定交叠,很难进行线性分类。为了更好目视识别地物信息,假彩色合成按近红外、红和绿波段顺序组合的图像如图2(a)所示。

对FCM算法,m=2,ε=10-6,Tmax=30。在无监督分类算法中,k-均值、FCM和KFCM算法的分类图分别如图2(b)～(d)所示。图2(b)中, k-均值算法把水和部分带阴影的植被分一类,把戈壁和雪分为一类,植被稀疏的为一类,生长旺盛的植被为一类。图2(c)中,FCM算法对水体、雪、戈壁都得到较好的分类,但带阴影的植被很多被错分为水。图2(d)中,KFCM算法比k-均值和FCM算法分类效果好,但也存在把少量带阴影植被错分为水和积雪较少的区域错分为戈壁。

在监督分类和半监督分类算法中,水体、植被、雪、戈壁的标记数据分别为745、890、912和915个。最大似然分类和MSVM以这些标记数据作为训练数据,而S3VM、SSFCM和SSKFCM算法以这些数据作为标记数据集 Xb。SSFCM和SSKFCM算法的参数m和ε与FCM算法相同。MSVM、S3VM、KFCM和SSKFCM算法的核函数取式(8)的径向基核函数,通过五重交叉验证, MSVM和S3VM算法的核参数σ=30、正则化参数C=100,S3VM算法的无标记数据的正则化参数C＊=100;KFCM和SSKFCM的核参数σ=1。最大似然、MSVM、S3VM、SSFCM和SSKFCM算法的分类图像分别如图2(e)～(i)所示。在图2(e)中,最大似然算法把有些带阴影植被和积雪较少的区域错分为戈壁。在图2(f)～(h)中, MSVM、S3VM和SSFCM算法对四类地物得到较好的区分,但也有少数植被分成水和戈壁,积雪较少的区域和戈壁也存在错分现象。在图2(i)中,SSKFCM算法对四类地物得到最好的区分,但SSKFCM算法也存在少量错分现象,这种错分现象比其他算法要少。图2(j)表示分类图2(b)～(i)中地物类别对应的颜色。

图2 北京一号小卫星图像和几种算法的分类图Fig.2 Beijing-1 micro-satellite image and the classification images of several algorithms on the image

4.2.2 结果对比与评价

为了定量评价几种算法的分类效果,以分类后的混淆矩阵为基础,计算用户精度、制图精度、总体分类精度和kappa系数。混淆矩阵是通过将感兴趣区的每个地表真实像元的位置和类别与分类图像中的相应位置和类别相比较计算的。这种感兴趣区不包括已标记的数据集。水体、植被、雪和戈壁的感兴趣区分别选取644、657、687和633个样本数据。表2给出了SSKFCM算法的混淆矩阵。

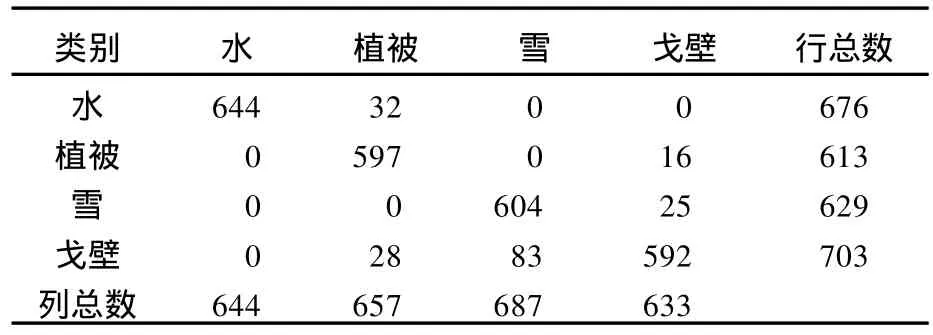
表2 SSKFCM算法的混淆矩阵Tab.2 Classification confusion matrix of the SSKFCM algorithm

其他算法的感兴趣区与SSKFCM算法相同。几种算法的性能比较如表3所示。

遥感图像分类的试验结果表明:无监督分类的KM算法的分类精度低于FCM和KFCM算法,FCM算法的分类精度低于KFCM算法;监督分类的ML算法的分类精度低于MSVM算法;半监督分类的S3VM和SSFCM算法的分类精度低于SSKFCM算法。SSKFCM算法的分类精度最高。

由于原始的SVM算法是针对小样本、非线性、高维数和局部极小点等两类问题提出来的,从表1和表3可以看出MSVM和S3VM算法在处理小样本集IRIS很占优势。但在处理大数据集的遥感图像数据时,MSVM和S3VM算法的分类结果不如SSKFCM算法,其主要原因:①由于多类SVM分类算法是由两类SVM算法推广而来,其本身存在如何提高推广能力的问题,推广到多类以后,多类SVM算法的不同最优化技术也产生不同的结果[17];②SVM算法在处理不可分情况引入惩罚参数C,以构造软间隔的最优超平面来分开样本,允许存在错分,但错分程度应尽可能的小,不同的错分程度影响其推广能力。在两个分类试验中,S3VM算法的结果逊于监督的MSVM算法的主要原因:MSVM算法的目标函数是凸问题,存在一个最小点;S3VM算法的目标函数中附加了无标记数据的惩罚项,使求解S3VM算法的目标函数变成一个非凸问题,存在多个极小点,寻找合适的解变得更加困难。文献[18-19]深入讨论了S3VM算法的非凸目标函数存在多个极小点的问题,以及非凸目标函数的几种最优化实现技术。

对比IRIS数据和遥感图像数据的分类结果,不管对小数据集的IRIS数据和大数据集的遥感图像数据,SSKFCM算法都显示了较强的分类能力。

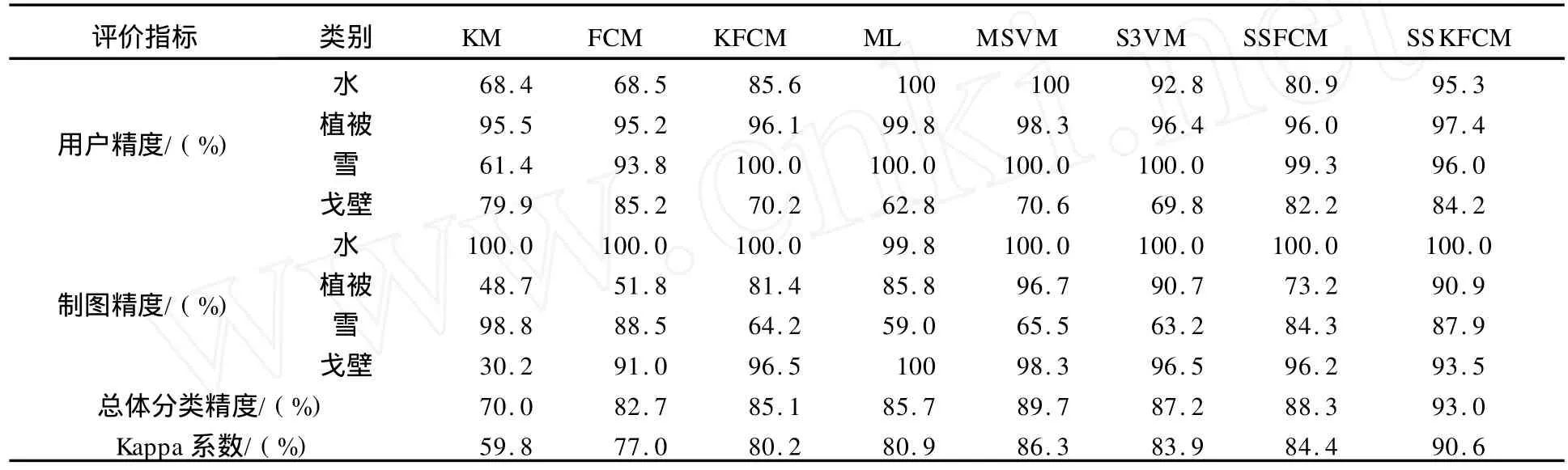
表3 几种算法的性能比较Tab.3 Performance comparison of several algorithms

5 结 论

由于遥感图像数据大多不服从高斯分布,以及遥感图像获取地面大量标记数据困难、分类存在模糊性和非线性等问题,传统分类方法在遥感图像分类中存在一定局限。本文提出用半监督核模糊c-均值算法对北京一号小卫星多光谱图像分类,取得了较好的效果。随着核理论的引入,输入特征向量被隐式地映射到高维空间,原来在低维空间非线性不可分模式在高维空间变成线性可分。通过半监督学习理论,在分类中使用标记数据指导未标记数据,从而提高了分类效果。因此,根据以上试验结果分析,把半监督学习理论和核理论引入FCM算法而形成的SSKFCM算法,能够提高北京一号小卫星遥感图像分类的精度。

[1] J ENSEN J R.Introductory Digital Image Processing:a Remote Sensing Perspective[M].3rd ed.Delhi:Pearson Education,2005.

[2] ZEN G Zhiyuan.Research on Computer Classification of Satellite Images and Application in Geoscience [M]. Beijing:Science Press,2004.(曾志远.卫星遥感图像计算机分类与地学应用研究[M].北京:科学出版社,2004.)

[3] BOUCHACHIA A,PEDRYEZ W.Enhancement of Fuzzy Clustering by Mechanisms of Partial Supervision[J].Fuzzy Sets and Systems,2006,157(13):1733-1759.

[4] LIU Yanfang,LAN Zeying,LIU Yang,et al.Multi-scale Evaluation Method forUncertainty ofRemote Sensing Classification Based on Hybrid Entropy Model[J].Acta Geodaetica et Cartographica Sinica,2009,38(1):82-87. (刘艳芳,兰泽英,刘洋,等.基于混合熵模型的遥感分类不确定性的多尺度评价方法研究 [J].测绘学报,2009, 38(1):82-87.)

[5] BEZDEK J C.Numerical Taxonomy with Fuzzy Sets[J]. Journal Mathemastical Biology,1974,1(1):57-71.

[6] BEZDEKJ C.Cluster Validity with Fuzzy Sets[J].Journal of Cybernetics,1973,3(3):58-73.

[7] PAL N R,BEZDEKJ C.On Cluster Validity for the Fuzzy c-means Model[J].IEEE Transactions Fuzzy on Systems, 1995,3(3):370-379.

[8] DUNN J C.A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact,Well-separated Clusters[J]. Journal of Cybernetics,1973,3(3):32-57.

[9] BEZDEK J C.Pattern Recognition with Fuzzy Objective Function Algorithms[M].New York:Plenum Press,1981.

[10] BEZDEKJ C,EHRLICH W F.FCM:The Fuzzy c-mean Clustering Algorithm[J].Computers and Geosciences, 1984,10(2-3):191-203.

[11] SCHOL KOPF B,SMOLA A J.Learning with Kernels [M].Cambridge:MIT Press,2002.

[12] GIROLAMI M.Mercer Kernel-based Clustering in Feature Space[J].IEEE Transactions on Neural Networks,2002, 13(3):780-784.

[13] BENSAID A M,BEZDEK J C,HALL L O,et al. Partially Supervised Fuzzy c-means Algorithm for Segmentation of MR Images[C]∥Proceedings of SPIE,Science of Artificial Neural Networks.San Diego:SPIE,1992: 522-528.

[14] ASUNCION A,NEWMAN D J.UCI Machine Learning Repository[DB/OL].[2010-01-18].http:∥www.ics. uci.edu/～mlearn/MLRepository.html.

[15] RICHARDS J A.Remote Sensing Digital Image Analysis [M].Berlin:Springer-Verlag,1999.

[16] HSU C W,LIN CJ.A Comparison of Methods for Multiclass Support Vector Machines[J].IEEE Transactions on Neural Networks,2002,13(2):415-440.

[17]CHI M,BRUZZONE L.Semisupervised Classification of Hyperspectral Images by SVMs Optimized in the Primal [J]. IEEE Transactions on Geoscience and Remote Sensing,2007,45(6):1870-1880.

[18] CHAPELLE O,CHI M,ZIEN A.A Continuation Method for Semisupervised SVMs[C]∥Proceedings of the 23rd InternationalConference on MachineLearning. New York:ACM,2006:185-192.

[19] SINDHWANI V,KEERTHI S,CHAPELLE O.Deterministic Annealing for Semi-supervised Kernel Machines [C]∥Proceedings of the 23rd International Conference on Machine Learning.New York:ACM,2006:841-848.

Classification for Beijing-1 Micro-satellite’s Multispectral Image Based on Semisupervised Kernel FCM Algorithm

LIU Xiaofang1,2,HE Binbin1,LI Xiaowen1
1.Institute of Geo-spatial Information Science and Technology,University of Electronic Science and Technology of China,Chengdu 610054,China;2.Department of Computer Science and Technology,Sichuan University of Science and Engineering,Zigong 643000,China

Most of remote sensing image data do not satisfy to Gauss distribution,and still the problems of the nonlinear,fuzziness and in lack of labeled data exist in the remote sensing image classification.A semi-supervised kernel fuzzy c-means(SSKFCM)algorithm is proposed to overcome these disadvantages.First,the SSKFCM algorithm is formed by involving semi-supervised learning technique and kernel method into the standard fuzzy c-means(FCM)algorithm.Then,IRIS data set and Beijing-1 micro-satellite’s multispectral images are classified by those algorithms,such as k-Means(K M),maximum likelihood(ML),multiclass support vector machines (MSVM),semi-supervised support vector machines(S3VM),FCM,kernel FCM(KFCM),semi-supervised FCM (SSFCM)and SSKFCM.Finally,the classification results are estimated by corresponding indexes.The results indicate that the SSKFCM algorithm significantly improved the classification accuracy of remote sensing images compared with the others.

remote sensing image classification;semi-supervised kernel fuzzy c-means algorithm;Beijing-1 microsatellite;kernel method;semi-supervised learning

LIU Xiaofang(1969—),female,PhD candidate,associate professor,majorsin remote sensing image processing and pattern recognition.

1001-1595(2011)03-0301-06

TP751

A

国家863计划(2007AA12Z227);国家自然科学基金(40701146);北京一号小卫星开放基金

(责任编辑:雷秀丽)

2010-01-05

2010-08-12

刘小芳(1969—),女,博士生,副教授,主要研究方向为遥感图像处理、模式识别。

E-mail:lxf1969@163.com.