一类线性算子半群的收敛性

禹晓红, 宋晓秋, 李玉霞

(中国矿业大学 理学院,江苏 徐州 221008)

一类线性算子半群的收敛性

禹晓红, 宋晓秋, 李玉霞

(中国矿业大学 理学院,江苏 徐州 221008)

为得到C0半群序列收敛于C0半群的条件,利用算子半群与无穷小生成元的关系,讨论了C0半群的收敛性和算子序列逼近问题。在 Banach空间上,借助无穷小生成元的强收敛性得出其生成半群的强收敛性。借助定义有界线性算子Ln,将该结论推广到了一般的Banach空间序列上,进一步完善了Banach空间上算子半群的收敛性理论。

C0半群;半群序列;无穷小生成元;收敛性;算子序列逼近;抽象柯西问题

0 引 言

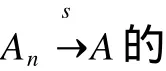
设X表示Banach空间,B(X)表示X上全体有界线性算子构成的Banach空间。

1 C0半群的收敛性

2 一般的 C0半群的收敛性

[1] PAZYA.Semigroupsof linearoperators and applications to partial differential equations[M].New York:Springer,1983.

[2] L I Y C,SHAW S Y.On generators of integratedC-semigroups andC-cosine function[J].Semigroup Forum,1993,47(1): 29-35.

[3] DELAUBENFELS R.C-semigroups and the cauchy problem [J].J FunctAnal,1993,111(1):44-61.

[4] L I Y C,SHAW S Y.N-times integratedC-semigroups and the abstract cauchy problem[J].Taiwanese Journal of Mathematics, 1997,1(1):75-102.

[5] 宋晓秋,彭爱民,王彩侠.C-半群与积分半群的概率型逼近[J].南京大学学报:数学半年刊,2003,20(2):215-225.

[6] 曹德侠,宋晓秋,荣 嵘.n次积分C半群的Laplace逆变换[J].徐州师范大学学报:自然科学版,2004,22(1):7-9.

[7] 李慧敏,宋晓秋,赵月英.双连续n次积分C余弦函数的逼近定理[J].应用泛函分析学报,2010,12(3):249-253.

[8] YOUNG S L.Covergence ofC-semigroups[J].Kangweon-KyungkiMath Jour,1998,6(1):9-15.

[9] 张祥芝,宋晓秋,刘钧文.n次积分C-半群的收敛性[J].中国矿业大学学报,2006,35(3):423-426.

Convergence of a kind of linear operator sem igroup

YU Xiaohong,SONG X iaoqiu,L I Yuxia
(College of Sciences,China University ofMining&Technology,Xuzhou 221008,China)

Aimed at enablingC0semigroup sequences to converge toC0semigroup,this paper discusses the convergence and operator series approximation ofC0semigroup using the relationship between operator semigroup and infinitesimal generator.In the space ofBanach,the strong convergence of infinitesimal generator results in the strong convergence of the generated semigroup.Besides,using the definition of a bounded linear operatorLn,makes it possible to extend the conclusion to the generalBanach space sequence,thus improving the convergence of semigroup in Banach space.

C0semigroup;semigroup sequence;infinitesimal generator;convergence;sequence of approximation operators;abstract Cauchy problem

O177.2

:A

1671-0118(2011)02-0161-02

2011-01-30

中央高校基本科研业务费专项资金资助项目(2010LKSX08)

禹晓红(1985-),女,山西省大同人,硕士,研究方向:应用泛函分析,E-mail:theyuxiaohong@126.com。

(编辑王 冬)