两类平图对应的链环分支数

周 靓 苹

(漳州城市职业学院 经济管理系，福建 漳州 363000)

两类平图对应的链环分支数

周 靓 苹

(漳州城市职业学院 经济管理系，福建 漳州 363000)

在纽结理论中，符号平图与链环投影图之间有着一一对应关系，图的对应的链环投影图的分支数与符号平图的符号无关，确定平图的对应的链环投影图的分支数是用平图研究链环的基本问题之一.给出并证明 8.8.6格图和 Aztec diamond图对应的链环分支数.

8.8.6格图；Aztec diamond图；链环；分支数；R-变换

0 引言

如果一个图能画在平面上使得它的边仅在端点相交，则称这个图为平面图.平面图的平面嵌入称为平图.一个符号平图指每条边都标有±号的平图.

在纽结理论中，链环分支数是链环的一个不变量，符号平图与链环投影图之间有着一一对应关系，图的对应的链环投影图的分支数与符号平图的符号无关.这就提供了用平图研究链环的一种方法，在20世纪80年代末，这种对应就被用于纽结理论的Jones多项式[1]和图论的Tutte多项式[2]之间的联系.

本文运用无符号平图的Reidemeister变换(以下简记为R-变换)给出并证明8.8.6格图和Aztec diamond图对应的链环分支数.

本文约定，G指符号平图，D(G)是图G对应的链环投影图，p(G)，q(G)和k(G)分别是图G的顶点数，边数和连通分支数.μ(D(G))是图G对应的链环投影图的分支数(也即图G对应的链环的分支数).则μ(D(G))与图G的符号无关，μ(D(G))也可看作是图G的中间图M(G)直走路数目.

下面是有关μ(D(G))的两个已知结论：

1）设G是一个平图，T(x,y)是G的Tutte多项式.则T(−1,−1 )=(− 1)q(G)(− 2)μ(D(G))−k(G).G是连通平图且

GG τ(G) =TG(1,1)是G的生成树数目，则μ(D(G))＝1当且仅当τ(G)是奇数.

2）G是无环平图，L(G)是G的拉普拉斯矩阵，则μ(D(G))等于L(G)的余秩.

从上述结论可知这样一个事实，由一个平图得到的链环的分支数不依赖于平面图的平面嵌入方式.

在纽结理论中，链环在三类 R-变换下不改变其分支数，而这三类变换正对应着符号平图的三类 R-变换，从而，这三类符号平图的 R-变换不改变平图的对应的链环分支数，且它对应着无符号平图的 R-变换.所以，可以用无符号平图的R-变换确定图的对应的链环分支数.

1 无符号平图的R-变换

无符号平图的R-变换(如图1):

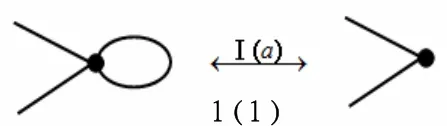
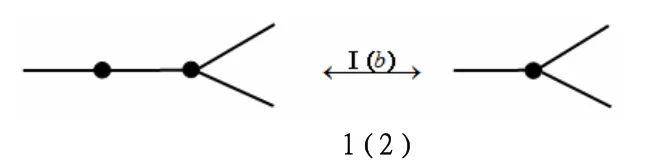
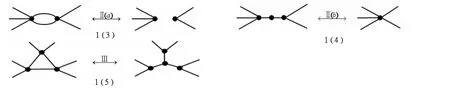
图1 平图的R-变换示意图

下面是有关无符号平图的R-变换的已知结论[3]:

引理1设G是平图.

下面给出无符号平图R-变换的等价类的定义.给定两个无符号图G和H，如果G能由R-变换及它的逆变换变换为H的同构图，则称G和H是 Reidemeister等价的.记为G~RH.由引理 1知平图的 R-变换不改变平图的对应的链环分支数，故若G~RH，则μ(D(G))＝μ(D(H)).

无符号平图的 R-变换 I(a),I(b),II(a),II(b)和III分别对应于对应的链环投影图所对应的无符号平图的Reidemeister的3种变换类型.根据Reidemeister定理和这样一个事实:任何链环投影图都能通过改变其交叉点的上下交叉关系使它变为平凡链环的投影图，可得到下面定理.

定理1G是一个平图，则μ(D(G))＝k当且仅当G能通过有限次无符号平图的R-变换变为空图Ok.

证明从上述结论，充分性显然.下面证必要性，适当地给图G标定符号，使D(G)是某个平凡链环的投影图.由Reidemeister定理，D(G)能变换为平凡链环的标准形式US，即通过有限次R-变换使它在平面上是一些不交圈的并.因平凡链环的标准形式US对应于空图Eμ(D(G)).因此，平图G可通过有限次无符号图的 R-变换，变换为空图Eμ(D(G)).定理得证.

2 8.8.6格图对应的链环分支数

定义1由四边形、六边形及八边形按如图2的方式叠加构成的平图称为8.8.6格图，记为Gm×n.

定理2设m,n是两个正整数，则μ(D(Gm×n))=2 +(m− 1)gcd(2,n)，其中gcd(2,n)为2和n的最大公约数.

证因Gm×n可由 R-变换变为m−1个不交的方格图和 2条不交的路Pn，如图3所示.又有μ(D(Pn))=1，μ(D(L2×n)) = gcd(2,n)，由定理1知，μ(D(Gm×n))=2μ(D(Pn)) + (m− 1)μ(D(L2×n))=2+(m− 1)gcd(2,n)，从而定理得证.

定义 2由 8.8.4格图增添加边(ai,bi)所得的平图称为循环边的 8.8.6格图，记为GmP×n.

图2 8.8.6格图

定理3设m,n是两个正整数，则

1) 当n是奇数时，=2 +(m− 1)gcd(4,n);

2) 当n是偶数时，=4 +(m− 1)gcd(4,n).

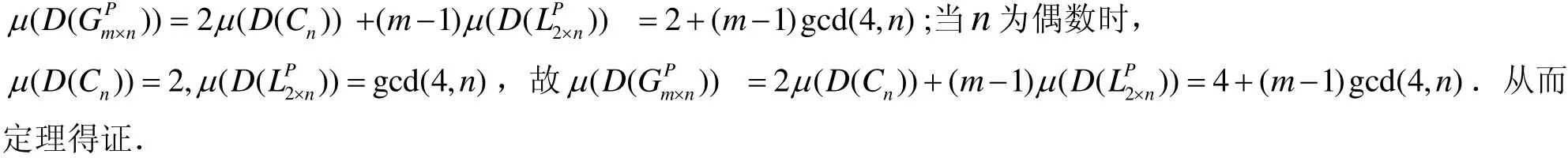
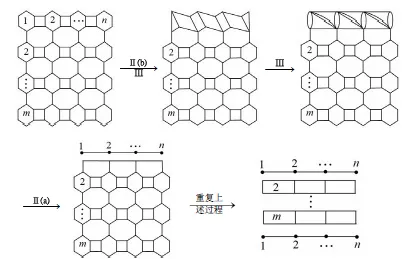
图3 证明定理2示意图

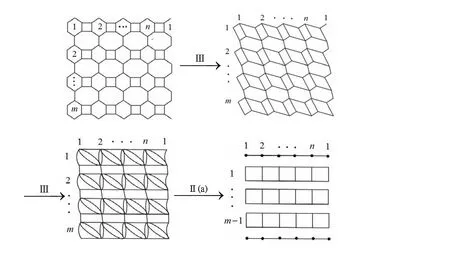
图4 证明定理3示意图

3 Aztec diamond图对应的链环分支数

定义3n阶Aztec diamond图是指一个关于第n行对称的，由2n−1行若干正方形的叠加所得，且第i行有2i−1个正方形(1≤i≤n)的平图，记为An[5].

图5分别是两个Aztec diamond图A2和A3.

定理4设n是一个正整数，则μ(D(An))=2n.

证 因An可由R-变换变为n个不交的4−圈C4，如图6所示，又μ(D(C4)) =2，由定理1知，μ(D(An)) =n×μ(D(C4))= 2n，从而定理得证.

例如A3对应的链环分支数为6，如图7所示.

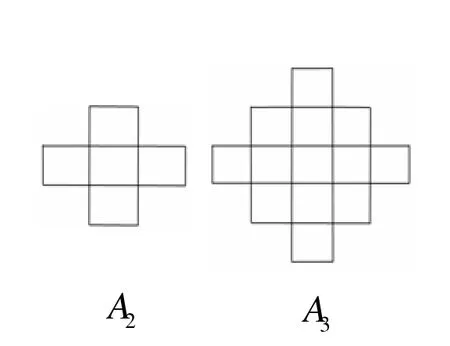
图5 Aztec diamond图

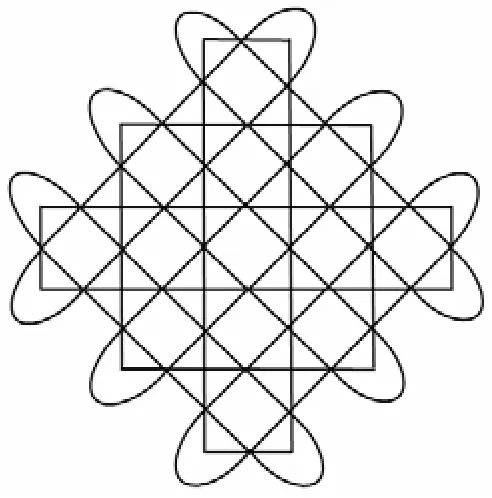
图7 A3所对应的中间图直走路数目是6

[1] JONES V F R. A polynomial invariant for knots via von Neumann algbras[J]. Bull.Amer.Math.Soc., 1985(12):103-111.

参考文献：

[1] JONES V F R. A polynomial invariant for knots via von Neumann algbras[J]. Bull.Amer.Math.Soc., 1985(12):103-111.

[2] TUTTE W T. A contribution to the theory of chromatic polynomials[J]. Canad.J.Math., 1954(6):80-91.

[3] JIN Xian-an.On graphs determining links with maximal number of components via medial construction[J]. Discrete Applied Mathematics, 2009,157:3099-3110.

[4] JIN Xian-an.Determining the component number of links corresponding to lattices[J]. Journal of Knot Theory and its Ramifications, 2009(12):1711-1726.

[5] ALFRED W. Covering the Aztec Diamond with One-sided Tetrasticks[EB/OL]. [2010-05-19]. http://did.mat.uni-bayreuth.de/ wassermann/tetrastick.pdf.

The Component Number of the Corresponding Link Diagram about Two Kinds of Plane Graphs

ZHOU Jing-ping
(Department of Economic Management, Zhangzhou City Vocational College, Zhangzhou, Fujian 363000, China)

In knot theory, there is a one-to-one correspondence between signed plane graphs and link diagrams via the medial construction. The component number of the corresponding link diagram is independent of the signs of the plane graph. Determining the component number of the corresponding link diagram may be one of the basic problems in studying links by using graphs. The paper gives and proves the component number of the corresponding link diagram about the 8.8.6-lattice graphs and the Aztec diamond-graphs.

8.8.6- lattice graphs; Aztec diamond-graphs; link; component number; Reidemeister move

O189.24

A

1673-2065(2011)04-0026-04

2010-05-19

周靓苹(1966-),女,福建漳州人,漳州城市职业学院经济管理系副教授.

(责任编校：李建明英文校对：李玉玲)