模糊层次分析法参数取值范围的修正

耿振杰，张卫东，黄青群

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.河池学院 数学系，广西 宜州 546300)

模糊层次分析法参数取值范围的修正

耿振杰1，张卫东1，黄青群2

(1.桂林电子科技大学 数学与计算科学学院，广西 桂林 541004;2.河池学院 数学系，广西 宜州 546300)

近年来，在多属性决策或群决策问题中，对于基于模糊互补判断矩阵的决策问题已受到了广泛的重视。对文献［1］和文献［2］给出的排序公式中的参数进行修正，得到更加合理的权重值，并举例对比分析了修正后的参数取值的合理性，是对排序公式进行的补充和完善。

模糊判断矩阵;排序;对比分析

0 引言

多属性决策是决策分析的重要组成部分，已经应用到人们生活与国防建设中的各个领域。如购买房子，需要综合考虑房子的价格、面积、层次、位置和周边环境等多种因素;选拔领导干部，既要考虑被选择人的品德和才能，又要考虑他的健康状况;选择炮兵阵地，火力发挥、疏散隐蔽、构工伪装、防御程度、道路状况这些诸多因素都是要整合考虑的;战时对多个部队单位的装备物资发出也需要综合许多因素，方能制定发出方案，决定应该先发给哪个部队、什么装备、物资数量质量等。虽然多属性决策问题的背景不同，但其实质均是利用已有的决策信息通过一定的方式在多个属性下对一组被选方案进行排序和择优。它在工程设计、经济、管理和军事等诸多领域中有着广泛的理论与实际应用背景，有着不小的研究实用价值。

20世纪70年代美国运筹学家A.L.Saaty教授提出了层次分析法(AHP)，为了改进传统层次分析法中诸如判断一致性与矩阵一致性相异、一致性检验困难与缺乏科学性等等问题以提高决策可靠性，一些学者提出了基于模糊一致矩阵的模糊层次分析法(FAHP)。目前，有关模糊判断矩阵的排序理论与排序方法的研究成果很多。Herrera－Viedma等在文献［3］中讨论了一致性模糊判断矩阵的性质，揭示了一致性模糊判断矩阵元素之间的关系。张吉军在文献［4］中推导了判断矩阵和权重之间的关系;吕跃进在文献［1］中对文献［4］进行了补充并推导了由判断矩阵求权重的排序公式;张吉军在文献［2］中对文献［1］进行了完善，提出了更为合理的排序公式。文献［5］和［6］对模糊判断矩阵的排序方法进行了总结，分析了其中一些方法的不足。本文主要是对文献［1］和［2］给出的排序公式中的参数进行修正，并举例说明。

1 模糊互补判断矩阵的排序公式

给出几个定义:

定义 1: 若矩阵 A=(ɑij)n×n满足:0≤ɑij≤1，i=1，2，…，n;j=1，2，…，n，则称 A 是模糊矩阵。

定义 2: 若模糊矩阵 A=(ɑij)n×n满足:ɑij+ ɑji=1，i=1，2，…，n;j=1，2，…，n，则称模糊矩阵 A 是模糊互补矩阵。

定义 3: 若模糊矩阵 A=(ɑij)n×n满足:对任意 i，j，k 有，ɑij= ɑik－ ɑjk+0.5 成立，则称模糊矩阵 A 是模糊一致矩阵。

定理1［5］: 设 A=(ɑij)n×n模糊互补判断矩阵，将 A=(ɑij)n×n按行求和，并令.作如下变换:

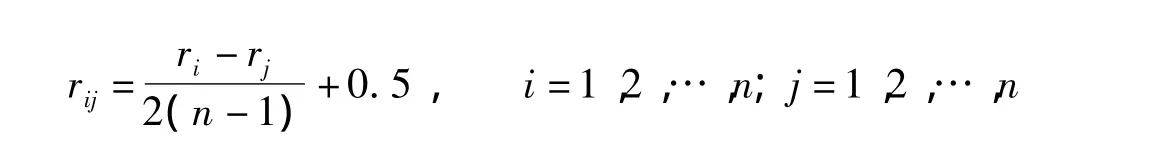
得到模糊一致判断矩阵 R=(rij)n×n，则由 R=(rij)n×n的元素 rij与权重 wi的关系式:rij=a(wi－wj)+0.5 求

得的权重向量 W=(w1，w2，…，wn)T满足:

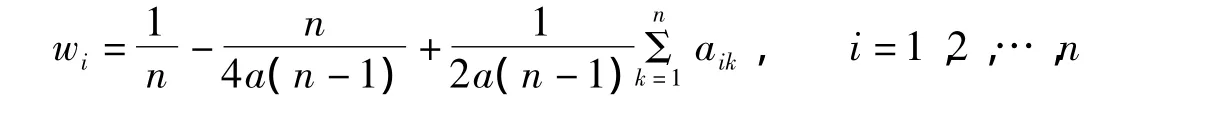
2 对参数ɑ的修正

我们研究发现，上述ɑ的取值范围是存在问题的。考虑下面一个问题:假设有四个足球队:巴西、老挝、越南、巴基斯坦，我们想知道这几个国家的权重，很容易被大家接受的是:0.7、0.15、0.1、0.05，众所周知，巴西是一个足球强国，单他一个国家的权重占0.7是易被接受的，甚至可以更大。如果用模糊层次分析法的排序公式:

3 举例对比分析

看下面一个例子:有四个因素 a1、a2、a3、a4、a1比 a2、a3、a4都极端重要，a2、a3、a4同等重要，由此得到的模糊互补矩阵为:

4 结论

本文通过对排序公式中参数a的修正，得到了更加合理的取值范围，权重取值因此也可以变的更大，权重之间的差异更加明显，利用对排序结果的灵敏度进行分析，对决策者作出正确的判断更加有利。

［1］吕跃进.基于模糊一致矩阵的模糊层次分析法的排序［J］.模糊系统与数学，2002，16(2):79－85.

［2］张吉军.模糊互补判断矩阵排序的一种新方法［J］.模糊系统与数学，2005，14(2):59－63.

［3］Herrera － Viedma E，Herrera F，Chiclana F，Luque M.Some issues on consistency of fuzzy preference relations［J］.Europen J.Oper.Res.，2004，154:98－109.

［4］张吉军.模糊层次分析法(FAHP)［J］.模糊系统与数学，2000，14(2):80 －88.

［5］樊治平，姜艳萍.模糊判断矩阵排序方法研究的综述［J］.系统工程，2001，19(5):12－18.

［6］宋光兴，杨德礼.模糊判断矩阵排序向量的确定方法研究［J］.模糊系统与科学，2004，18(2):73－82.

［7］王莲芬，许树柏.层次分析法引论［M］.北京:中国人民大学出版社，1989.

［8］Tanino T.Fuzzy preference orderings in group decision making［J］.Fuzzy sets and Systems，1984，12:117 －131.

［9］姚敏，张森.模糊一致矩阵及其在决策分析中的应用［J］.系统工程理论与实践，1998，18(5):78－81.

［10］姚敏，黄燕君.模糊一致关系及其应用［J］.电子科技大学学报，1997，26(6):632 －635.

［11］徐泽水.一种改进的模糊一致性判断矩阵构造方法［J］.应用数学与计算数学学报，1996，11(2):62－67.

A Modified Parameter Range for FAHP

GENG Zhen-jie1，ZHANG Wei-dong1，HUANG Qing-qun2
(1.School of Mathematics and Computing Science，Guilin Univerersity of Electronic Technology，Guilin，Guangxi 541004;2.Department of Mathematics，Hechi University，Yizhou，Guangxi 546300，China)

In recent years，for multiple attribute decision － making or group decision － making problems，the decision－making problems based on fuzzy complementary judgement matrix have been attached wide attention to.This article corrects the parameter in the sort formula in the literature［1，2］and gains a more reasonable weight.It also illustrates and makes a comparative analysis of the rationality of revised parameters，which supplements and perfects the ranking method for fuzzy complementary judgement matrix.

fuzzy judgement matrix;ranking;comparative analysis

O159;C934

A

1672－9021(2011)02－0005－04

耿振杰(1984－)，男，河南开封人，桂林电子科技大学数学与计算科学学院硕士研究生，主要研究方向:优化理论及其应用。

国家自然科学基金资助项目(11061011);广西高校优秀人才计划项目(〔2009〕156)。

2010－12－18

［责任编辑 刘景平］