New isoconversional method for evaluating unambiguous activation energy values for solid decomposition
2011-12-22HANYunqingLIUNaian
HAN Yun-qing,LIU Nai-an
(State Key Laboratory of Fire Science,University of Science and Technology of China,Hefei,230026,China)
韩运晴,刘乃安
(中国科学技术大学火灾科学国家重点实验室,安徽合肥,230026)
New isoconversional method for evaluating unambiguous activation energy values for solid decomposition
HAN Yun-qing,LIU Nai-an*
(State Key Laboratory of Fire Science,University of Science and Technology of China,Hefei,230026,China)
A new isoconversional method based on the modified Vyazovkin method is proposed to evaluate the activation energy for solid-state reactions.This method is used without any pre-knowledge of reaction mechanisms and overcomes the limitation of current isoconversional methods that they fail to give unambiguous activation energy values like model-fitting methods.This method was tested in both of simulated data and experimental data of extruded polystyrene decomposition,which showed that this method had good tolerance of experimental noise and was proved to be more effective than model-fitting methods to extract reliable activation energy values those multiple reactions whose first-order derivative of thermogravimetric data turn out distinct maximums.
Isoconversional method;Model-fitting method;Activation energy
1 Introduction
Solid decomposition is widely related to lots of fields.For example,solid decomposition is a forerunner process of the combustion of flammable solids,and therefore,the study of solid state reactions is meaningful in the field of fire science.In the past decades,both model-fitting and isoconversional(model free)methods for extracting kinetic parameters of solid reactions by isothermal or nonisothermal experimental data have been greatly developed,but with different merits and limitations in methodology.
Model-fitting methods often involve in fitting different reaction models(Table 1)to a single conversion curve or multiple curves and simultaneously determining the unambiguous activation energy Eand pre-exponential factorAby regression analysis.The critical comments on model fitting methods mainly argued that results of the kinetic parameters ofEandAmay vary greatly with different reaction models and there are no good criteria to distinguish the best result[1-5].
Comparatively,isoconversional methods[6-9]are capable to evaluate the activation energy without any prior knowledge of model function but the values usually vary with the degree of conversion.Note that for single step reactions,the variable activation energy calculated by isoconversional methods may result from some random effects such as the perpetuation of nominal heating rate caused by self-cooling/heating effects,the experimental noises,the imperfection of experimental samples,experimental facilities and so on[10-12]. Although such variable activation energy is helpful to demonstrate the complexities of a reaction,it doesn’t correlate any activation step and thus seems to have obvious conflict with general chemistry theoryand has become one of the controversial points[13-15].Galwey[13]questioned the meaning of variable activation energy and concluded as follows:“the proposed introduction of this term,E(variable),is a retrograde step,unlikely to advance science through the development of theory and its use is not recommended.”

表1 表述固体反应动力学的常见反应模型Table 1 Set of reaction models to describe the reaction kinetics in solid state reactions
Though some new methods were developed in recent years[16-18],it seems that isoconversional methods still fail to extract unambiguous activation energy like model-fitting methods.This problem was solved by an isoconversional method proposed in this work,which can give more reliable unambiguous activation energy values than model-fitting methods.The method was tested by both simulative and experimental data.
2 Theoretical analysis
Nearly all the model-fitting and isoconversional methods are based on the general differential kinetic equation of solid-state reaction,

or its integral form

whereA(min-1)is the pre-exponential factor,E(kJ/mol)the activation energy,Rthe gas constant,andT(K)the absolute temperature.The functionfα is the so-called“model function”which relates to the reaction mechanism,andgα is the integral of the reciprocal of the model function.
The modified Vyazovkin method[6]assumesE to be constant only for a small segmentΔ αand uses integration over small time segments for Eq.(2),

The procedure points out for a given conversion and a set of experiments performed undernarbitrary heating programs:

Numerically,after cancelingAα,the value of Eαcan be determined by minimizing the following function:
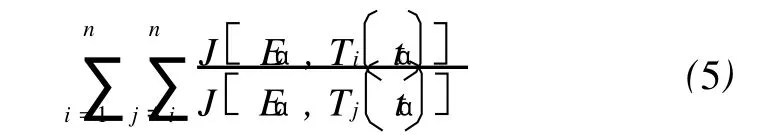
On the Vyazovkin’s isoconversional method,theJ-integrals[Eq.(4)]forssmall segments gives,

and then after cancelingAα,Eq.(6)can be reduced to the condition of a minimum:

For the casesEis a constant,Eq.(7)can be represented as a condition of minimum value:

Substituting the timetα,for which a given conversion has been reached and the actual temperature at the moment into Eq.(8)and varyingEuntil attaining the minimum gives an estimate of the unambiguous activation energy.Obviously,this work is finished without any further assumption of model-free methods.
3 Simulation analysis
This section will verify the advantage of the new isoconversional method by numerical and experimental examples.
3.1 Simulation for an one-step reaction
Three runs of simulations(A,BandC)were generated at four heating rates(β=2,4,6,8 K/min)with E=130kJ/mol andA=1014min-1.SimulationAis error-free using a first-order model,fα =1-α.To simulate the case that reaction model of real experiments may be uncovered in the present model list,SimulationBuses an unexpected model function,fα = 1-α3/2.It’s well known that in many cases,the determination of the temperature values close toα=0 and/or to α=1 are susceptible to rather high errors,so we consider the estimating of activation energy for those two Simulations in both full reaction extents(α =0-1)and partial extents(α =0.1-1).
The levenberg-Marquardt nonlinear model-fitting method in the software of NETZSCH thermokinetics[19]was used by adopting various model functions respectively,the activation energy values(E)and correlation coefficients(r)of which as well as the unambiguous activation energy values determined by our model-free method was displayed in Table 2.It can be seen that for SimulationAandB,F1 provides right values(Eandr),but the coefficients of R2 and R3 are also practically acceptable. ForSimulation B,two reaction models(F1 and F2)provide good correlation coefficients but neither of them gives the right activation energy value.Moreover,it’s shown that the values ofEand rdetermined by model-fitting methods are different for full extents(0≤α≤1)and partial extents(0.1 ≤α≤1).So it’s not an easy work to tell which value can be selected by model-fitting methods.In contrast,the isoconversional method provided in this work always gives the right activation energy values(130kJ/mol).
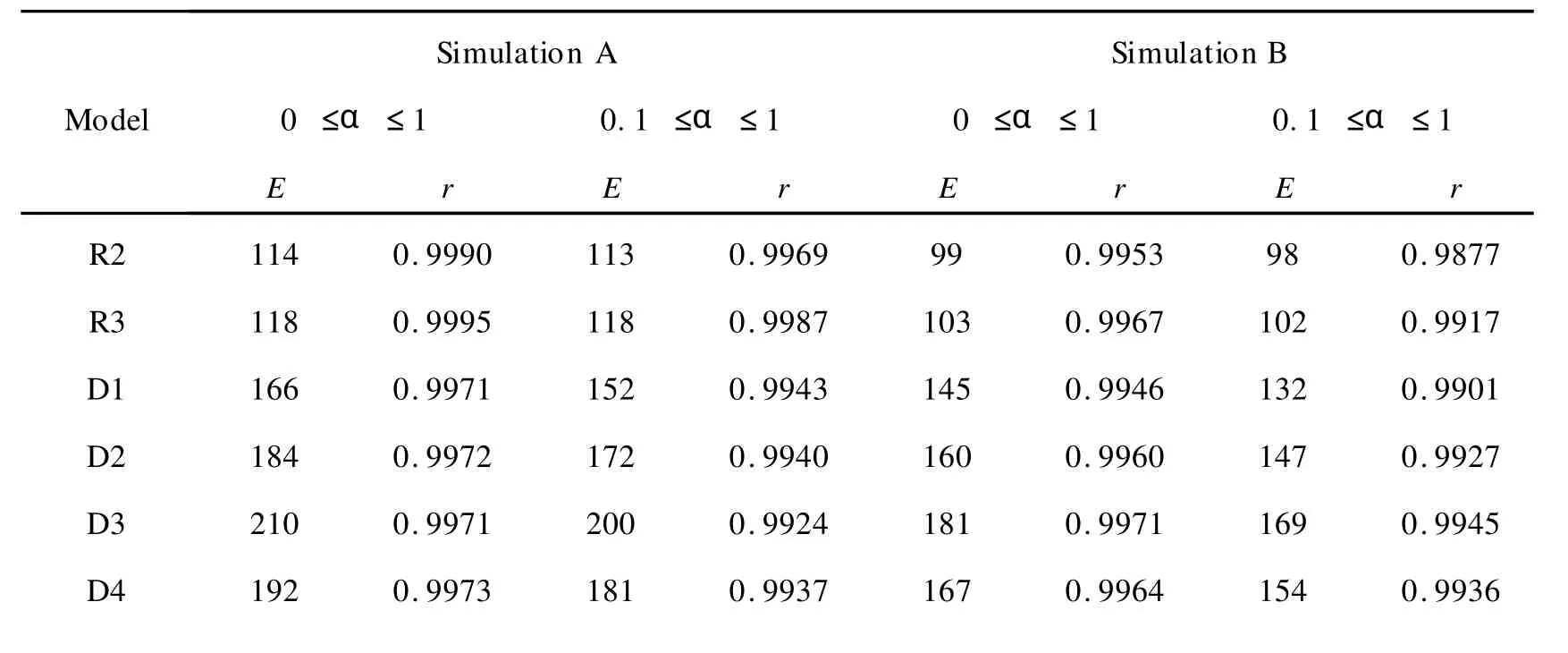
表2 使用levenberg-Marquard非线性拟合法以及我们的等转化率方法对单步反应求解获得的相关系数(r)和活化能(EkJ/mol)Table 2 Model-fitting correlation coefficients(r)and activation energy values(EkJ/mol)for the simulated one step reaction evaluated by levenberg-Marquardt nonlinear model-fitting method and our model-free method

F1 130 1 130 1 112 0.9990 111 0.9972 F2 177 0.9974 181 0.9924 153 0.9993 154 0.9981 Ours 130 —— 130 —— 130 —— 130 ——
In addition,to approximate the variability encountered in real data,error(±0.5K random error)were introduced to SimulationCfor each heating programs.The values ofEwere obtained by AIC is shown in Fig.1.It can be seen that the activation energy values scatter seriously.However,the value given by our method(129.36kJ/mol)is practically same as the preset value(130kJ/mol).

图1 使用AIC方法对模拟过程C求解获得的活化能的值Fig.1 Activation energy values evaluated for the simulated process C by AIC method
It is worth mentioning that although the models are simulated in linear heating programs,the method suggested can be applied to an arbitrary variation of temperature as well as to isothermal conditions by replacing β dα/dT withdα/dtin relevant equations.
3.2 Determining unambiguous activation energy values for some multistep reactions
In this part,a process that involves two independent parallel reactions,which lead to a variation in the effective activation energy,is simulated.The overall kinetic equation of this process is described as:
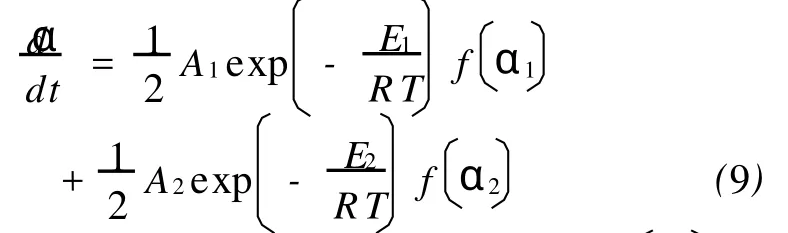
whereE1=120kJ/mol,A1=109min-1,fα1=
1-α1(F1),E2=160kJ/mol,A2=1014min-1,fα2= 1-α22(F2).
The thermogravimetric curves were calculated for four heating rates(2,4,6 and 8K/min)(Fig.2.a). Through numeric differentiation of thermogravimetric curves,the curvesdα/dT vs.T were plotted(Fig.2.b).Fig.2.b shows that each of thedα/dT vs.Tcurves exhibits two maximums.As is shown in Fig.3,FR and AIC lead to practically same values but the values for 0.45<α<0.70 are lower than the activation energies of both reactions.
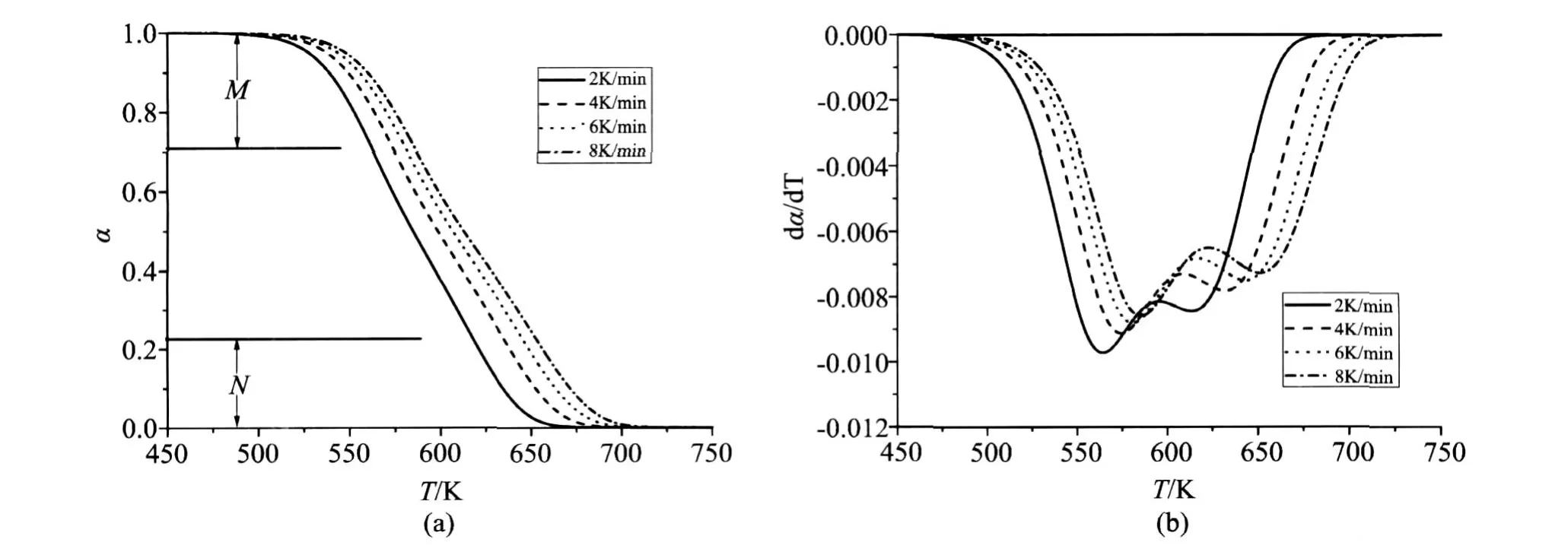
图2 模拟的平行反应的α~ T曲线及两个选择区间(a),和dα/dT~ T曲线(b).Fig.2 α~ Tcurves and two ranges selected,(a),anddα/dT~ Tcurves,(b),for simulations of two parallel independent reactions
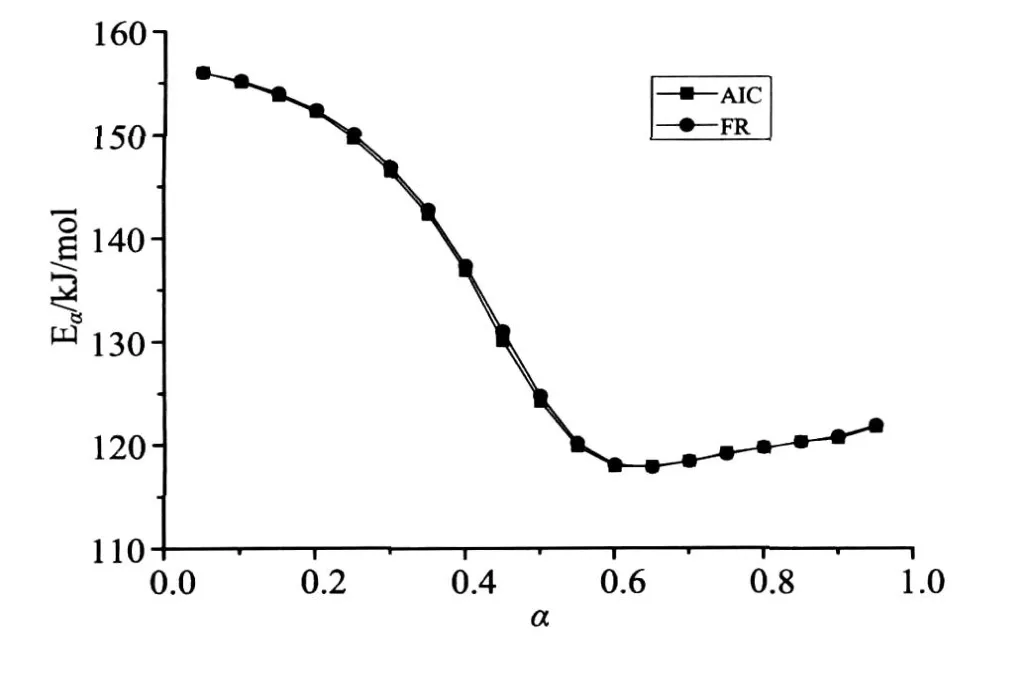
图3 使用等转化率方法求解模拟的平行反应获得的活化能随转化率变化的曲线Fig.3 Dependence of the apparent activation energy evaluated by model-free methods on the conversion degree,for simulated two parallel reactions
The method proposed in this work is helpful to tell unambiguous values of activation energies for such parallel reactions whose first derivative with respect to thermogravimetric curves have two apparent maximums.Empirically,it can be finished by the two steps:(1)determine the two particularαvalues of each curves corresponding to the two maximums ofdα/dt~ Tplots;(2)pick out the biggest value among the four values of the first maximum and the smallest one of the second maximum for the four curves.
The two particularαfor the simulated four lines are 0.688,0.264;0.701,0.249;0.708,0.242;0.712,0.230 and so 0.712 and 0.230 is selected for the first and second maximum respectively.Then the two activation energy values can be determined by our method(Eq.(8))within the two range of 0≤α≤0.230 and 0.712≤α≤1(Fig.2.a),which gives 154.17 and 120.26kJ/mol.Compare to the setting values(160 and 120kJ/mol)their deviations(3.64%and 0.22%)do not exceed 5%of the commonly acceptable level.polystyrene was used as-supplied by Anhui Jingang Energy Saving Technology Co. Ltd. Sample weighted from 9.31 to 10.65 mg.The actual values of heating rates were calculated from the recorded sample temperature against time.
The activation energy determined by regular model-free method is shown in Fig.4.It can be seen that the activation energy values vary with the degree of conversion.The values of activation energy and the correlation coefficient obtained by model-fitting method are shown in Table 3.Obviously,it’s not easy to distinguish R2,R3 and R1 as their correlation coefficient are all bigger than 0.99.Moreover,their values of activation energy are all bigger than any point of the values obtained in Fig.4.This probably because the activation energy doesn’t obtained by the experimental data directly but by the assumed pre-knowledge of model function and so the pre-exponential factor makes a compensation effect[20,21]in the process.While using the method proposed in this work,an unambiguous value of 161.8kJ/mol can be given for the reaction,which is well within the range of the variable activation energy values in Fig.4.
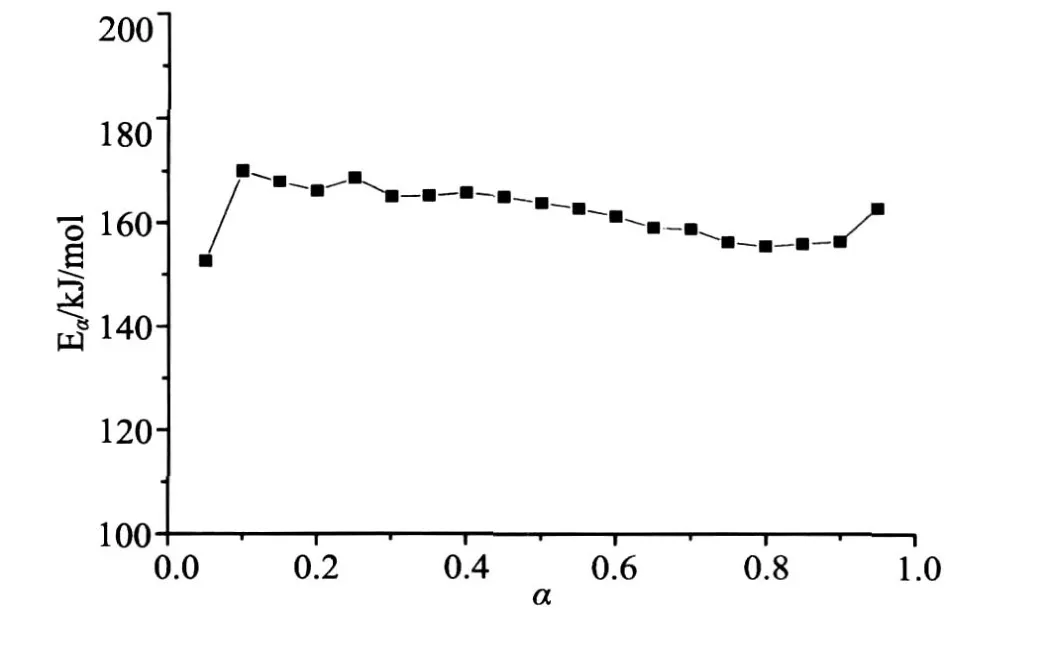
图4 使用改进的Vyazovkin方法对挤塑聚苯乙烯的热解实验求解获得的活化能随转化率变化的曲线Fig.4 Dependence of the apparent activation energy evaluated by the modified Vyazovkin method on the conversion degree for the decomposition of extruded polystyrene
4 Experimental analysis
The thermal decomposition of extruded polystyrene was carried out in a 50 ml/min flow of N2at 5,10,20 and 40K/min from room temperature(300K)to 1100K on a Shimadzu DTG-60H Simultaneous TGA/DTA Analyzer.The extruded
5 Conclusions
Based on the modified Vyazovkin method,an isoconversional method seeking to extract unam-biguous activation values like model-fitting methods has been developed.The method is fulfilled without any further assumption of current isoconversional methods and has great advantage over the current model-fitting methods:firstly,it can be used without any pre-knowledge of model function;secondly,it can be applied to partial information of the whole data freely.Examples also show that the method has good tolerance for experimental noises and provides more reliable activation energy values than model-fitting methods.
This work may helpful in enlarging the applied range of isoconversional methods and,theoretically,relating to the general theoretical principles that are applicable throughout chemistry.
This work was sponsored by National Natural Science Foundation of China under Grants 51076148 and R&D Special Fund for Public Welfare Industry(forestry,200704027).Naian Liu was supported by the Fok Ying Tung Education Foundation.Haixiang Chen was supported by National Natural Science Foundation of China under Grant 50806070.

表3 使用levenberg-Marquard非线性拟合法以及我们的等转化率方法对挤塑聚苯乙烯的热解实验求解获得的相关系数(r),活化能(EkJ/mol)和指前因子(A1×1010min-1)Table 3 Model-fitting values of correlation coefficients(r),activation energy(EkJ/mol)and pre-exponential factor(A1×1010min-1)for the decomposition of extruded polystyrene evaluated by levenberg-Marquardt nonlinear model-fitting method and our model-free method
[1]Vyazovkin S.Computational aspects of kinetic analysis.Part C.The ICTAC Kinetics Project-the light at the end of the tunnel?[J].Thermochimica Acta,2000,355(1-2):155-163.
[2]Roduit B.Computational aspects of kinetic analysis.Part E:The ICTAC Kinetics Project-numerical techniques and kinetics of solid state processes[J].Thermochimica Acta,2000,355(1-2):171-180.
[3]Brown M E,et al.Computational aspects of kinetic analysis:PartA:The ICTAC kinetics project-data,methods and results[J].Thermochimica Acta,2000,355(1-2):125-143.
[4]Burnham A K.Computational aspects of kinetic analysis.Part D:The ICTAC kinetics project-multi-thermalhistory model-fitting methods and their relation to isoconversional methods[J].Thermochimica Acta,2000,355(1-2):165-170.
[5]Maciejewski M.Computational aspects of kinetic analysis.Part B:The ICTAC Kinetics Project-the decomposition kinetics of calcium carbonate revisited,or some tips on survival in the kinetic minefield[J].Thermochimica Acta,2000,355(1-2):145-154.
[6]Vyazovkin S.Modification of the integral isoconversional method to account for variation in the activation energy[J].Journal of Computational Chemistry,2001,22(2):178-183.
[7]Ozawa T.A New Method of Analyzing Thermogravimetric Data[J].Bulletin of the Chemical Society of Japan,1965,38(11):1881-1886.
[8]Flynn J H and Wall L A.A quick,direct method for the determination of activation energy from thermogravimetric data[J].Journal of Polymer Science Part B:Polymer Letters,1966,4(5):323-328.
[9]Friedman H.Kinetics of thermal degradation of charforming pastics from thermogravimetry-application to a phenolic resin[J].J Polym Sci Part C:Polum Lett 6:.1964,183-195.
[10]Vyazovkin S and Wight C A.Kinetics in solids[J].An-nual Review of Physical Chemistry,1997,48:125-149.
[11]Khawam A and Flanagan D R.Role of isoconversional methods in varying activation energies of solid-state kinetics-II.Nonisothermal kinetic studies[J].Thermochimica Acta,2005,436(1-2):101-112.
[12]Khawam A and Flanagan D R.Role of isoconversional methods in varying activation energies of solid-state kinetics-I.isothermal kinetic studies[J].Thermochimica Acta,2005,429(1):93-102.
[13]Galwey A K.What is meant by the term’variable activation energy’when applied in the kinetic analyses of solid state decompositions(crystolysis reactions)?[J].Thermochimica Acta,2003,397(1-2):249-268.
[14]Galwey A K.Is the science of thermal analysis kinetics based on solid foundations?:A literature appraisal[J].Thermochimica Acta,2004,413(1-2):139-183.
[15]Laidler KJ.The development of the Arrhenius equation[J].Journal of Chemical Education,1984,61:494.
[16]Rotaru A and Gos,a M.Computational thermal and kinetic analysis[J].Journal of Thermal Analysis and Calorimetry,2009,97(2):421-426.
[17]Ortega A.A simple and precise linear integral method for isoconversional data[J]. Thermochimica Acta,2008,474(1-2):81-86.
[18]Wanjun T and Donghua C.An integral method to determine variation in activation energy with extent of conversion[J].Thermochimica Acta,2005,433(1-2):72-76.
[19]Opfermann J.Kinetic analysis using multivariate nonlinear regression-I.Basic concepts[J].Journal of Thermal Analysis and Calorimetry,2000,60(2):641-658.
[20]Vyazovkin S and Wight C A.Isothermal and nonisothermal reaction kinetics in solids:In search of ways toward consensus[J].Journal of Physical Chemistry A,1997,101(44):8279-8284.
[21]Koga N.A Review of the Mutual Dependence of Arrhenius ParametersEvaluated by the Thermoanalytical Study of Solid-State Reactions-the Kinetic Compensation Effect[J].Thermochimica Acta,1994,244:1-20.
1004-5309(2011)-0009-07
2010-09-26;修改日期:2010-10-21
韩运晴,男,中国科学技术大学火灾科学国家重点实验室硕士研究生。主要研究方向为森林与城市火灾。
刘乃安,研究员,E-mail:liunai@ustc.edu.cn.
面向固体热解单一活化能计算的等转化率动力学分析方法研究
基于改进的Vyazovkin方法,提出了一种新的求解固态反应活化能的等转化率方法。这种方法不仅避开了对反应机理的选择,而且突破了当前等转化率方法不能像拟合法一样求解出明确的活化能的局限。通过对模拟数据及挤塑聚苯乙烯热解实验数据的验证,证实了这种方法对实验噪音具有良好的容许度,并且能够对热重数据的一阶导数据有明显的多峰多歩反应求解出比拟合法更可信的活化能的值。
等转化率方法;拟合法;活化能
O 643.13
A
韩运晴,刘乃安
(中国科学技术大学火灾科学国家重点实验室,安徽合肥,230026)
