基于博弈论的道路交叉口信号灯设置标准

陈富坚，郭忠印，柳本民，陈富强

（1.同济大学 交通运输工程学院，上海201804；2.桂林电子科技大学 建筑与交通工程学院，桂林541004）

城市道路平面交叉口交通管制方式主要分全无控制、主路优先控制、信号灯控制和环形设置等几种方式，其中信号灯控制是城市道路交叉口最普遍的交通管理形式.信号灯设置得当，可以改善交叉口的交通秩序，提高交叉口的通行效率和交通安全状况；信号灯设置不当，非但浪费了设备及安装费用，且对交通还会造成不良的后果［1］.因此，制定科学合理的交通信号灯设置标准有重要的现实意义.目前，美国的《统一交通控制设施手册》［2］及我国的《道路交通信号灯设置与安装规范》（GB14886—2006）［3］规定的设置交通信号灯条件的主要理论分析依据是交通量与延误，此外，还有学者提出采用交通冲突分析法来确定机动车信号灯设置标准［4］.鉴于设置交通控制信号的理论分析方法目前尚未统一，因此，对其设置标准作进一步的理论研究还是有必要的.

道路交叉口各方冲突的实质是争夺有限的时空资源，一方得到意味着另一方失去，因此，他们之间的关系本质上是存在利益相互依存性的博弈关系.目前，博弈论在交通领域［5-8］已有应用，但在道路交叉口信号灯设置标准方面，尚未见文献报道.本文以博弈论为基础，建立道路交叉口斗鸡博弈模型，并采用混合策略纳什均衡分析方法和有限理性进化稳定策略分析方法来分析模型的解，以此导出交叉口信号灯的设置标准，并通过示例和参数变化分析来说明结果的合理性.

1 交叉口博弈的建模及其解的分析

交叉口冲突交通流之间的博弈可分为两部分：冲突机动车流之间的博弈以及冲突机动车流与人流或非机动车流（为简化，后面提及行人的内容都包括非机动车）之间的博弈.根据博弈论［5］，机动车间的博弈可看作双人对称斗鸡博弈，行人与机动车间的博弈可认为是双人非对称斗鸡博弈.因此，交叉口博弈可分解为双人对称斗鸡博弈和双人非对称斗鸡博弈两部分，下面分别予以分析.

1.1 机动车之间的双人对称斗鸡博弈

1.1.1 模型的建立

假设：一方采取冒进策略而另一方采取礼让策略时双方的得益分别为b和-b（以一个城市车辆的平均时间价值计算，b为正数）；当双方都采取冒进策略时会引起两败俱伤，此时双方的得益都是-a（以一个城市的平均交通冲突损失计算，a为正数且远大于b）；当双方都采取礼让策略时双方的得益均为-b.显然，机动车间的博弈是完全信息静态博弈［5］，见表1.表中的下划线是采用划线法分析博弈均衡解的标志.下同.

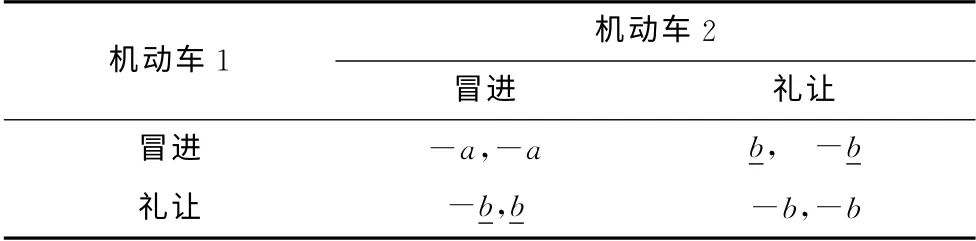
表1 双人对称博弈模型Tab.1 Symmetrical chicken game model

采用划线法分析得益矩阵可知，该博弈是一个多重纳什均衡博弈，存在两个纯策略纳什均衡，分别为：机动车1冒进和机动车2礼让，及机动车1礼让和机动车2冒进.从表1还可看出，对于这两个纳什均衡，双方的偏好完全不一致，利益是冲突的.在非合作博弈框架内，这两个纳什均衡是不稳定的，不能作为斗鸡博弈模型的解，需要寻找另外的具有稳定性的解，即均衡策略.根据纳什定理［9］，此模型应当还存在一个混合策略纳什均衡，即博弈双方以一定的概率分布随机选择冒进与礼让两种策略进行博弈，这个混合策略纳什均衡才是斗鸡博弈模型的稳定解.因此，现在的关键问题是求出这个混合策略纳什均衡解，即计算出各博弈方分别选择冒进和礼让两种策略的最佳概率分布.下面对此进行分析.

1.1.2 双人对称斗鸡博弈的混合策略均衡解

根据理性经济人假定和混合策略均衡的策略选择原则［9］，博弈方1的最佳策略是逼对方选择礼让而自己得以通过，即自己选择冒进策略的概率最好让对方选择冒进策略的期望得益与选择礼让策略的期望得益相等，从而使对方不得不礼让；由于博弈方2与1的地位是对称的，当双方都采取这种策略时，博弈便达到混合策略纳什均衡局势.设博弈方1采用冒进策略的概率为Pj，则采取礼让策略的概率为1-Pj.由于地位对称性，则博弈方2采用冒进策略和礼让策略的概率也分别为Pj和1-Pj.

博弈方2各种策略的得益函数为：

冒进策略的期望得益：

礼让策略的期望得益：

根据上述均衡原则，博弈方1的最佳策略为所选择的Pj满足：

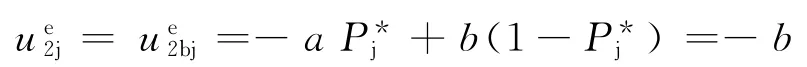
解该方程，得博弈方1的最佳策略为：P＊j=2b／（a+b），1-P＊j=（a-b）／（a+b）；根据对称性可知，这也是博弈方2的最佳策略.画出博弈方1采取冒进策略的得益函数图像，则所求解得到的最佳策略即是得益函数与x轴的交点，如图1所示（图中a′，b′是根据相关参数变化后的a，b）；对博弈方2同样如此.因此，当博弈方1和2分别采取P＊j=2b／（a+b）和1-P＊j=（a-b）／（a+b）作为冒进和礼让策略的概率时，博弈达到混合策略纳什均衡的稳定状态，在此状态下，任何一方单独改变策略都将不能改善自己的期望得益.此状态下双方发生冲突的概率：

根据纳什（Nash）的混合策略群体行为解释［9］，相互冲突机动车流的司机对混合策略（冒进和礼让两种策略的概率）的选择，可以理解为一个地区或城市的交通事故发生频率和该地区中谨慎和冒进两种类型驾驶员的比例，混合策略均衡就是上述频率和比例之间的平衡关系.

图1 博弈方1的混合策略Fig.1 Mixed strategies of No.1player

下面对混合策略纳什均衡局势下交叉口博弈的系统整体效益ue进行分析：

式中，ue1和ue2分别为博弈方1和2的期望得益.

可以看出，混合策略纳什均衡局势下交叉口博弈的整体效益与双方都采取礼让策略时的系统总得益相等，都是-2b，差于两个纯策略纳什均衡局势下博弈系统的总得益（都是0）.因此，引入系统外的相关均衡机制（信号灯）是很有必要的，以便以轮换的方式轮流实现两个纯策略纳什均衡来提高交叉口博弈系统的整体社会效益，问题的关键是确定引入信号灯均衡机制的临界点.

根据上述群体行为解释，可以将混合策略均衡状态下的交通冲突率4b2／（a+b）2理解为一个城市或地区道路交叉口的平均交通安全状态.当某个道路交叉口的交通冲突率高于该城市的平均交通冲突率4b2／（a+b）2时，意味着该交叉口的交通冲突现象比较严重，博弈效率差，需要引入交通信号灯来实现更有效率的均衡.因此，4b2／（a+b）2可作为交叉口信号灯设置标准来参考.

1.1.3 交叉口斗鸡博弈的进化博弈分析

根据复制动态分析方法，设x为一个城市的所有机动车司机中采用冒进策略的博弈方（冒进型司机）的比例，则1-x为采用礼让策略的博弈方（保守型司机）的比例，那么，采用两种策略博弈方的期望得益uje和群体平均期望uebj得益分别为：

根据上述得益函数可得复制动态方程如下：

根据进化稳定策略的定义和微分稳定原理［9-10］可知，符合要求的进化稳定策略是满足以下方程组的解：

满足F（x）=0 的解有三个：x＊1=0（全是保守型），x＊2=1（全是冒进型）和x＊3=2b／（a+b）（两种类型各占一定的比例）.计算可知x＊3=2b／（a+b）是真正的进化稳定策略.

上述进化博弈分析结果的现实意义是，在交叉口的长期进化博弈中，冒进型博弈方的数量比例最终会稳定在总数量的2b／（a+b）左右水平，这意味着：①一方礼让另一方通过交叉口的概率是（4ab-4b2）／（a+b）2；②发生交通冲突的概率会稳定在4b2／（a+b）2左右的水平；③双方由于无法判断对方的策略而都采取礼让的保守策略时的概率为（a-b）2／（a+b）2，其实，出现这种情况意味着司机是较谨慎的，其结果是绝大部分会转化为①，即一方礼让另一方通过.总之，②③两种状态都会导致交叉口通行能力某种程度的损失.随着交叉口流量的增加，发生②③两种状态的总数量也逐步增大，所导致的交叉口通行能力损失和生命财产损失也逐步增大.当某交叉口斗鸡博弈所导致的社会损失增大到该市的平均交通损失水平4b2／（a+b）2时，可认为该交叉口开始进入被过度利用的低效率状态，此时应当在交叉口设置交通信号灯来提高通行效率和经济效益.因此，1.1.2得到的标准从进化博弈的角度看是合理的.

1.2 机动车与行人间的双人非对称斗鸡博弈

1.2.1 模型的建立

当考虑斗鸡博弈模型得益矩阵中双方的损失不相等时，博弈就变为非对称条件下的双人斗鸡博弈，此时可理解为机动车与行人博弈.博弈模型如表2所示，表中每一个得益数组的第1个数字为机动车司机的得益，第2个数字为行人的得益.得益矩阵中行人采取礼让策略的负得益以期望礼让时间乘以所在城市居民的平均时间价值进行计算.

综合两口井资料，气水内边界线的作图深度平均为-5 140m，气水外边界线的作图深度平均为-5 175m。

表2 非对称条件的斗鸡博弈模型Tab.2 Asymmetrical chicken game model

同理分析可知该博弈存在两个纯策略纳什均衡和一个混合策略纳什均衡，且只有混合策略纳什均衡才是合理解.

1.2.2 双人非对称斗鸡博弈的混合策略纳什均衡解

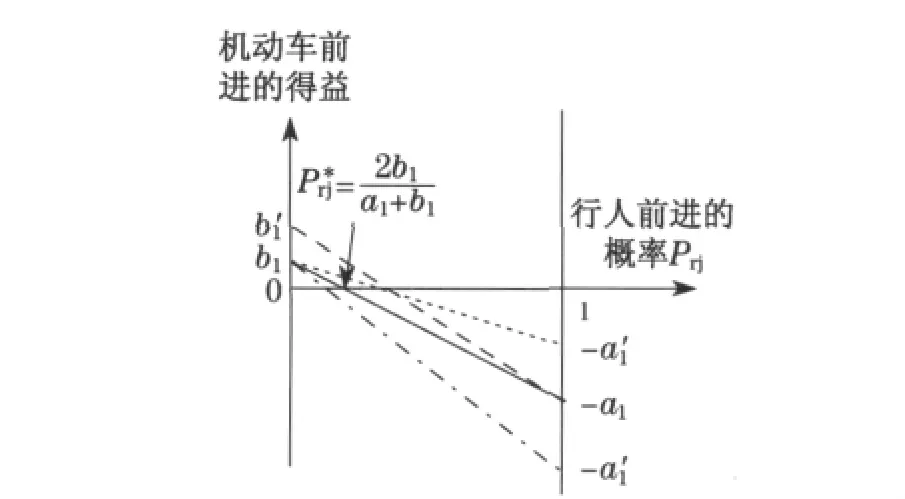
图2 斗鸡博弈中行人的混合策略Fig.2 Mixed strategies of pedestrian in chicken game

图3 斗鸡博弈中机动车司机的混合策略Fig.3 Mixed strategies of drivers in chicken game

同理可求得双人非对称条件下发生交通冲突的概率为

1.2.3 非对称条件下的两人斗鸡博弈的进化分析

同样采用大群体成员随机配对复制动态进化机制进行长期博弈的进化稳定策略分析.设强势方群体中冒进型的比例为x，则强势方群体中谨慎型的比例为1-x；设弱势方群体中冒进型的比例为y，则弱势方谨慎型的比例为1-y.分别求出强势方群体和弱势方群体的复制动态方程如下：

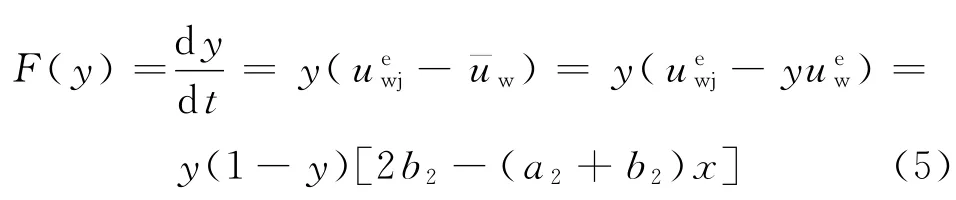
根据复制动态方程（4）和（5），可分析强势方和弱势方两个群体互动关系下的联合进化稳定策略，见图4.根据图4箭头所示的进化收敛方向可看出，在非对称斗鸡博弈的长期进化博弈中，当初始情况落在A 区时会收敛到进化稳定策略x＊=0、y＊=1，即强势博弈方都采取保守策略而弱势博弈方都采取冒进策略；当初始情况落在D 区时会收敛到进化稳定策略x＊=1、y＊=0，即强势博弈方都采取冒进策略而弱势博弈方都采取保守策略；当初始情况落在B和C 两个区域时，会收敛到x＊=2b2／（a2+b2）、y＊=2b1／（a1+b1），这是混合策略均衡状态，是不稳定性的，有可能向A 或D 区转化.

图4 非对称斗鸡博弈群体复制动态和稳定性Fig.4 Replicator dynamics of asymmetrical chicken game

由于一般有b1远小于a1，b2远小于a2，且a1小于a2（现实意义为交通事故对机动车司机意味着经济损失而对行人意味着生命损失或重伤），则图4中A 和D 两个区域的面积实际上是非常小的，且A 远小于D，B区域占了整体封闭区域面积的绝大部分.这表明非对称斗鸡博弈的长期趋势收敛于D.但对于非长期博弈的冲突概率，式（3）作近似计算是合理的，因此，可作为行人信号灯的设置标准.

2 转换为交通冲突数的信号灯设置标准

综合上述对称和非对称斗鸡博弈分析，可以式（1）和式（3）分别作为交叉口机动车和行人专用信号灯设置标准.当一个交叉口的相应交通冲突率分别达到式（1）和式（3）规定值的水平时，应考虑设置相应的信号灯.为方便实际操作，此处对式（1）和式（3）在四路交叉口和三路交叉口中具体化，转换为以交通冲突数为单位的计算标准.对于图5的四路交叉口，其有12股机动车流，具有斗鸡博弈特征的有8股，共16个博弈点.对于图6的三路交叉口，具有斗鸡博弈特征的机动车流有3股，共3个博弈点.图5和图6的四路交叉口和三路交叉口中，行人过街有可能遇到6股机动车流，由于左转与直行车流往往能合并，可简化为4股车流，实际博弈点可认为有4个，则行人与机动车间的斗鸡博弈数为过街行人数的4倍.设交叉口每年的机动车和行人流量分别为Qsj，Qr，并假定交通流在各流向均匀分布，则求得相应的交通冲突数为：

图5 十字路交叉口博弈位置图Fig.5 Game spots at crossroad intersection

图6 三路交叉口博弈位置图Fig.6 Game spots at T-shape intersection

对于十字交叉口：

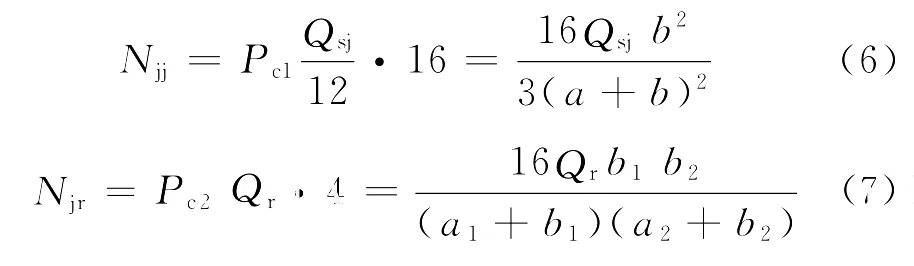
式（6）～（7）中，Njj，Njr分别为交叉口机动车间冲突数和机动车与行人间冲突数.

对于三路交叉口：

如果能调查得到式（6）～（9）中交通冲突损失平均值，并选定合适的年交通量作临界值，代入式（6）～（9）可得交叉口博弈导致的年交通冲突总数.鉴于现实中有大量的轻微交通冲突没有进入交警部门的事故统计档案或没有上报［12］，因此，应根据实际调查得到的交通事故数和交通冲突数的比例进一步将式（6）～（9）的计算结果换算为交通事故数，作为操作性更强的信号灯设置标准.

3 应用示例

据统计，2007年上海市一般处理程序以上交通事故损失费平均为4 900元·次-1，城市车辆的平均时间价值为127元·h-1，上海市居民的人均时间价值为18元·h-1.假定没有进入交警部门事故统计档案的轻微交通冲突的数量是进入交通事故处理档案的交通事故数量的10倍，则每起交通冲突中各方平均损失为223元；假定无信号交叉口对称博弈中一方礼让另一方通过的期望时间为3s，则机动车时间价值b为0.20元，非对称博弈中机动车礼让行人的期望时间为5s，行人礼让机动车的期望时间为3s，则机动车时间价值b1和行人的时间价值b2分别为0.31元和0.02元.将各值代入式（1）和（3），即得可作为上海市道路交叉口信号灯设置标准值的年交通冲突率（次冲突·10-6·车辆数-1）：

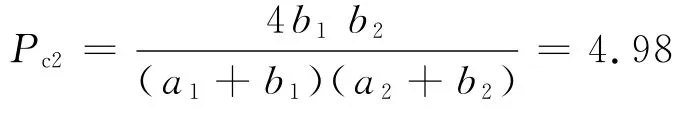
我国现行国标［3］的4.11条安装信号灯的依据为：双向机动车车道数达到或多于3条，双向机动车高峰小时流量超过750pcu 以及12h 流量超过8 000pcu的路段上，当通过人行横道的行人高峰小时流量超过500人次时，应设置人行横道信号灯及相应的机动车道信号灯.现计算该流量条件下四路交叉口的期望交通事故数.假定在上述条件下交叉口24h的机动车流量和行人流量分别为10 000辆·d-1、6 000人·d-1，求解可得交叉口一年内发生一般处理程序以上的机动车间的期望交通事故数为1.4起，机动车和行人间的期望交通事故数为4.4起，两者合计约6起.因此，4.11条信号灯安装依据在上海本地化后可转换为：当交叉口一年内发生一般处理程序以上的交通事故总数达到6起及以上程度时，可考虑设置信号灯.显然，转换后的规定与该规范的4.9.1条很接近.因此，博弈论可以将两者在本质上统一起来.

4 斗鸡博弈模型参数变化的影响分析

4.1 b，b1，b2 变化的影响分析

从图1～图3可看出，当各博弈方的得益b，b1，b2增大（虚线所示）而相应的损失水平不变时，任一博弈方想迫使对方让路必须加大采取冒进策略的概率，这必然引发交叉口交通冲突概率的增加，所导致的交通事故损失和交叉口通行能力损失也跟着加大.其现实意义是：当交叉口的交通流量增大且交通流结队通过交叉口的情况较普遍时，抢先获得通过的一方将获得较大的时间价值得益，而礼让的一方被迫等待更长的排队时间.作为经济理性人的各博弈方自然更不愿意礼让，而倾向于采取更冒进的 “抢行”策略，从而导致交叉口的交通事故率增加，直到局面达到新的纳什均衡状态，式（2）表明，此时博弈系统的整体效率更差.因此，对于交通管理部门，选择合适的纳什均衡点，即交通冲突率作为设置信号灯的标准，一方面避免交叉口交通安全状况的恶化和通行效率的降低，另一方面避免过早设置信号灯所带来的问题.

4.2 a，a1，a2 变化的影响分析

从图1～图3 可以看出，加大某博弈方的损失a，a1，a2（点划线所示）而相应的得益水平b，b1，b2不变时，另一博弈方可以更小的冒进策略概率就能达到让对方让路的目的，礼让行为出现的概率更大.下面结合无过错免责原则与交通事故处理法规进一步阐述图1～图3的现实意义.

对于机动车间的对称斗鸡博弈，双方都是强者，地位对称，发生交通事故时双方都受损，因此，对事故责任的处理应秉承公平原则，实行过错方负全责而无过错方免责，过错方还应对无过错受损方进行赔偿，这实质是加重对违规行为的处罚，图1 表明，可促进交通礼让行为，降低事故率.

对于机动车与行人间的非对称斗鸡博弈，行人与机动车间发生冲突时，行人非死即重伤，而机动车方一般完好无损，故对这类交通事故，如果也实行无过错免责原则，相当于加大行人的损失而减少机动车方的损失，机动车方会更强悍更冒进，迫使行人让路所需要的冒进策略的概率更小（图3），而行人方如要迫使机动车方让行则必须加大采取冒进策略的概率（图2）.因此，无过错免责原则的实际效果是行人总体上更容易让行而机动车方则更强悍，总体上交通冲突率会明显降低；但是，由于机动车方更强悍，往往缺乏必要的谨慎，特别是无过错情况下的行为克制，在人口密集的城市必然会导致恶性交通事故率的增加.典型的例子是我国北方某城市实施无过错免责的《行人与机动车道路交通事故处理办法》（俗称 “撞了白撞”法规），实施此规则的城市几年间尽管交通秩序明显好转，但恶性交通事故率不降反增［13］.因此，如果要求无过错机动车方对非故意撞车的行人的伤害负一定责任，其效果如同图2所示的加大机动车方的损失，则必然会使得机动车方更为克制和警惕，对降低恶性交通事故率、体现 “人本” 精神有促进作用.

5 结论

（1）道路交叉口博弈的实质是相互冲突的交通流争夺有限的时空资源，一方得到意味着另一方失去，基于博弈论的交叉口信号灯设置标准综合考虑了交叉口交通量、博弈效率和社会损失等多方面因素，从本质上将以交通量或交通事故数为依据的信号灯设置标准统一起来，可作交叉口信号灯定量设置标准参考.

（2）传统上计算无信号交叉口通行能力的“空档”理论模型，因没考虑交叉口博弈中存在的交通冲突和相互礼让（通常表现为减速观望）两种状态下的通行能力损失而偏大，特别是概率很大的相互礼让状态下的通行能力损失.从博弈论角度看，需要对所得的通行能力计算结果进行适当的折减.

（3）在交叉口博弈中，无过错免责原则对于机动车间的对称博弈所导致的交通事故的处理是公平的，能有效抑制交通冲突率并促进交通文明；然而，对于机动车与行人间的非对称博弈交通事故，无过错免责原则尽管总体上能降低交通冲突率、提高通行效率，但却使得作为强者的机动车方更冒进强悍，缺乏必要的警惕和行为克制，从而导致行人死伤的非对称博弈恶性交通事故率不降反增.

［1］ 吴兵，李晔.交通管理与控制［M］.3 版.北京：人民交通出版社，2005.WU Bing，Li Ye.Traffic management and control［M］.3rd ed.Beijing：China Communication Press，2005.

［2］ U S Department of Transportation， Federal Highway Administration.Manual on uniform traffic control devices for streets and highways［R］.Washington D C：US Department of Transportation，Federal Highway Administration.2009.436-446.

［3］ 公安部.GB14886—2006 道路交通信号灯设置与安装规范［S］.北京：中国标准出版社，2006.2-4.Ministry of Public Security of P R China.GB14886—2006 Specifications for setting and installation of road traffic signals［S］.Beijing：China Standards Publishing House，2006.2-4.

［4］ 杨晓光，蒲文静，龙亮.基于交通冲突分析的交叉口机动车信号灯设置［J］.同济大学学报：自然科学版，2005，33（12）：1596.YANG Xiaoguang，PU Wenjing，LONG Liang.Traffic signal warrant study based on traffic conflict analysis for uncontrolled intersections［J］.Journal of Tongji University：Natural Science，2005，33（12），1596.

［5］ Fudenberg D，Tirole J.Game theory［M］.Cambridge：The MIT Press，1991.65-79.

［6］ Bell MG H，Cassir C.Risk-averse user equilibrium traffic assignment：An application of game theory［J］.Transportation Research Part B：Methodological，2002，36（8）：671.

［7］ CHEN O J W，Ben-Akiva ME.Game-theoretic formulations of interaction between dynamic traffic control and dynamic traffic assignment ［J］.Transportation Research Record，1998（1617）：179.

［8］ FISK C S.Game theory and transportation systems modeling［J］.Transportation Research Part B，1984，18（4／5）：310.

［9］ 谢识予.经济博弈论［M］.上海：复旦大学出版社，2007.70-86.XIE Shiyu.Economic game theory［M］.Shanghai：Fudan University Press，2007.70-86.

［10］ Smith J M.Evolution and theory of games［M］.Cambridge：Cambridge University Press，1982.10-21.

［11］ Nowak MA，Sigmund K.Evolutionary dynamics of biological games［J］.Science，2004，303（5659）：793.

［12］ 郭忠印，方守恩.道路安全工程［M］.北京：人民交通出版社，2003.123-126.GUO Zhongyin，FANG Shouen.Road safety engineering［M］.Beijing：China Communications Press，2003.123-126.

［13］ 吴坤.以人为本的立法典范［R／OL］.2004-10-18.http：／／www. people. com. cn／GB／14576／28320／39478／39480／2926464.html.WU Kun.Amodel for people-centered legislation［R／OL］.2004-10-18.http：／／www.people.com.cn／GB／14576／28320／39478／39480／2926464.html.