柱体限制失稳形态的统一挠度曲线方程

武秀根，郑百林，贺鹏飞，刘曙光

（1.同济大学 土木工程学院，上海200092；2.同济大学 航空航天与力学学院，上海200092）

工程结构中，为提高轴向受压柱的极限承载力，常常在失稳柱的外围布置限制其失稳波形发展的限制构件［1-2］，失稳位移受到限制，因而能继续承载.

轴向受压柱的限制失稳问题，属于后屈曲的范畴，其承载能力和后屈曲形态有极大的关系.Chateau等［3］对存在单侧限制的弹性结构的分岔和稳定性问题进行了一般意义上的研究，采用能量原理建立平衡方程.吕和祥等［4］引入拉格朗日乘子，采用数学规划法计算了外部受限制结构的临界载荷.Domokos等［5］在1997 年研究了压柱在两平行、刚性、光滑的约束面之间的后屈曲行为，分析了柱与刚性面之间的不同接触状态.Herzl Chai［6］采用聚碳酸酯材料制作细长的受压柱，使受压柱在刚性面之间发生限制失稳，观察细柱的失稳波形及其演化.申波等［7］研究了双钢管构件在受轴向压力时，内、外弹性变形构件之间由点接触状态到线接触状态之间的连续过渡过程中，接触力等变量的连续变化.

本文根据点接触和线接触的概念，在大变形框架下，引入截面转角作为统一变量，推导了点、线接触状态下的受压柱失稳形态方程.结果表明，不同的接触状态下，柱的失稳形态具有相同的方程形式，根据截面转角变量的不同取值范围区分不同的接触状态.

1 分析模型

以一平面轴向受压柱为研究对象.柱受压发生欧拉失稳后，两侧的失稳变形受到约束，进入后屈曲阶段，如图1所示.图中，为柱所受的轴向力，为柱的原始长度，为柱未受压时，距离两侧约束壁面的距离.

为计算及分析方便，做量纲一化处理［7］，各种变量的量纲一化约定如下：

该量纲一化公式里的变量并不代表后续分析中的具体变量，仅规定了当具体模型的变量类型为力、弯矩和位移时应分别采用的量纲一化方法.

由于两端约束的对称性，因此柱的各段失稳挠曲线也具有对称性或反对称性，因此可以选择具有代表性的部分挠度曲线进行分析，然后根据对称性或反对称得到整个柱的后屈曲挠度曲线.

2 挠度曲线方程的求解

2.1 点接触过程

点接触过程中，存在两典型柱段的变形：靠近端部的柱的挠度和中间部分柱的挠度.

分别在两典型柱段的反弯点建立局部坐标系，如图2～图4所示.根据对称性，取典型柱段的一半分析，C为段的反弯点，也即中点，D为段的反弯点，也即中点.点B，E为柱与约束壁面之间的接触点，坐标系Cx1y1为在C点建立的局部坐标系，坐标系Dx2y2为在D点建立的局部坐标系.分别用，表示，的水平距离.

图3中，s1为C到B点的弧长，则的长度为2s1，在反弯点处的量纲一剪力记为μ1，在s=0（即C点处）柱截面转角为θa，端点B的坐标为（a／2，h／2），λ为量纲一轴向力.图4中，s2为D点到B点的弧长，则的弧长为2s2，在s=0（即D点处）柱截面转角为θb，端点B在x2Dy2处的坐标为（b／2，h）.μ2 为D点处量纲一剪力.

2.1.1 端部挠度曲线

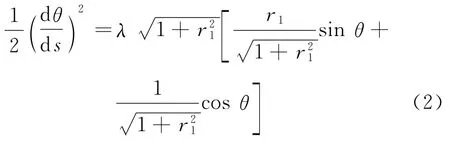
显然，当s=0时,，由式（3）得

其中，K（p1）为第一类完全椭圆积分，F（φ（s），p1）为第一类不完全椭圆积分［8］，

因为x=∫cos（θ（s））ds，y=∫cos（θ（s））ds，又φ=θ-α，故由式（4）可得

其中，E（p1）=

E（p1）为第二类完全椭圆积分，E（φ，p1）为第二类不完全椭圆积分.

2.1.2 中间部分挠度曲线分析

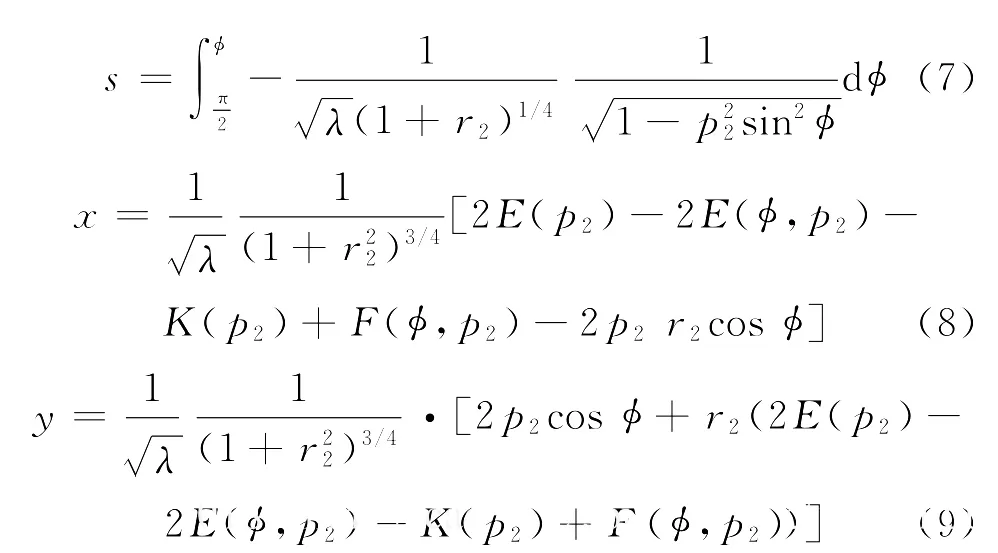
2.2 线接触过程

柱与约束面之间的线接触过程，柱的挠度可分为三部分典型的变形（图5）：靠近固定端的端部柱的挠度，柱与约束面之间的直线接触段，中间部分柱的挠度.依据与点接触相同方法，可以建立线接触过程各部分的挠度曲线方程.

图5 线接触过程，局部分析坐标系的建立Fig.5 Establishment of local analysis coordinate under point line contact state

3 点接触和线接触过程挠度曲线方程的比较

可以发现，虽然推导过程不同，但点接触过程与线接触过程中的长度以及直角坐标的表达式在形式上存在着统一性.

以端部挠曲线为例，点接触过程中，长度以直角坐标的表达式分别为式（4）～（6）.线接触过程，相应的计算式分别为式（7）～（9）.

可以发现，点接触过程和线接触过程中，长度以及直角坐标的计算式在形式上完全相同，当s=0时，都存在.区别在于点接触过程中，，其中θα为反弯点处截面转角.而线接触过程中，时，点接触过程，而线接触过程，

反弯点截面转角θa和参数φ（s1）随轴向载荷的变化曲线见图6和图7.

从点接触，线接触的计算公式比较可以看出，线接触的计算公式可以退化到点接触.当式（7），（8）和（9）中的φ（s1）＞-时，为点接触计算表达式，当φ（s1）=-时，为线接触计算表达式.中间部分典型柱的挠度曲线方程存在着同样的特点，点接触和线接触过程的挠度曲线方程均相同，依靠参数φ（s1）的不同取值确定不同的接触状态.

图6 反弯点处截面转角θa 的变化示意图Fig.6 Relationship between axial load andθa

图7 接触点处参数φ（s1）变化示意图Fig.7 Relationship between axial load andφ（s1）

4 结论

本文在大变形框架下，通过合理的建立局部分析坐标系，引入典型柱反弯点的截面转角作为变量，得到了失稳柱的挠度曲线方程.引入反弯点处的截面转角作为变量后，点接触和线接触状态下的挠度曲线方程可以采用统一的表达式形式，而截面转角不同的取值即决定了柱的不同接触状态.

采用统一的表达式形式描述柱在不同接触状态下的限制失稳波形，不仅可以简化分析过程，减少分析变量，而且对进一步研究柱失稳形态的连续变化过程和截面转角大于临界值，导致发生失效等极限失稳状态提供了便利.

［1］ 郭英涛，任文敏.关于限制失稳的研究进展［J］.力学进展，2004，34（1）：41.GUO Yingtao，REN Wenmin.Some advances in confined buckling［J］.Advances in Mechanics，2004，34（1）：41.

［2］ 武秀根，郑百林，贺鹏飞.限制失稳柱的后屈曲分析［J］.同济大学学报：自然科学版，2009，37（1）：26.WU Xiugen，ZHENG Bailin，HE Pengfei.Study on postbuckling of constrained bar［J］.Journal of Tongji University：Natural Science，2009，37（1）：26.

［3］ Chateau X，Nguyen Q S.Buckling of elastic structures in unilateral contact with or without friction［J］.Eur J Mech，A／Solid，1991，10（1）：71.

［4］ Lu Hexiang，Feng Minghui，Lark R J，et al.The calculation of critical buckling loads for externally constrained structures［J］.Communications in Numerical Methods in Engineering，1999，15（3）：193.

［5］ Domokos G，Holmes P，Royce B.Constrained euler buckling［J］.Journal of Nonlinear Science，1997，7（3）：281.

［6］ CHAI Herzl.The post-buckling response of a bi-laterally constrained column［J］.Journal of the Mechanics and Physics of Solid，1998，46（7）：1155.

［7］ 申波，邓长根.双钢管构件由点接触到线接触的连续过渡［J］.工程力学，2007，24（2）：154.SHIN Bo，DENG Changgen.Buckling of line-contact segment between axially compressed inner core and flexible sleeve in a sleeved column［J］.Engineering Mechanics，2007，24（2）：154.

［8］ 铁木辛科.弹性稳定理论（中译本）［M］.北京：科学出版社，1965.49-51.Timoshenko S P.Theory of elastic stability［M］.Beijing：Science Press，1965.49-51.

［9］ Roman B，Pocheau A.Postbuckling of bilaterally constrained rectangular thin plates［J］.Journal of the Mechanics and Physics of Solids，2002，50（11）：2379.