顾及2 套坐标误差的三维坐标变换方法

李微晓 ,沈云中 ,李博峰

(1.同济大学 测量与国土信息工程系, 上海200092;2.淮海工学院 测绘工程学院, 江苏连云港222001;3.现代工程测量国家测绘局重点实验室, 上海200092)

运用全球定位系统(GPS)技术建立控制网涉及到三维坐标变换模型.三维坐标转换通常采用7 个转换参数, 即3 个平移参数、3 个旋转参数和1 个尺度参数.根据旋转与尺度参数参考点的不同定义,三维坐标转换模型可分为:Bursa-Wolf 模型(简称Bursa 模型)、Molodensky 模型及武测模型等[1].然而,利用最小二乘方法求解这些模型时通常只采用1组公共点坐标改正数向量, 而不是对2 套坐标的公共点误差分别引入改正数进行解算,因此, 求得的改正数向量不能用于对任何一套坐标进行误差改正,以免引起公共点与待转换点坐标之间的缝隙, 除非对待转换点坐标的误差也作相应的改正.事实上,若能同时考虑2 套坐标的误差, 在求解转换参数时,求得2 套坐标的改正数并进行改正, 并用最小二乘配置法(least-squares collocation,LSC)推估待转换点的坐标改正数并进行改正, 有望提高转换坐标的精度.LSC 由K rarup 于1969 年在研究重力异常时提出[2] .1973 年奥地利的Moritz 进行了深入研究, 提出带系统参数的LSC[3].从20 世纪80 年代以来,我国学者对该理论进行了广泛深入的研究.周江文提出了LSC 模型的两步解法[4];杨元喜等讨论了基于方差分量估计的自适应LSC 模型,并将其应用于高程系统转换和地理信息系统(GIS)误差纠正[5];李博峰指出LSC 模型的理论基础是极大验后估计,实质是采用观测值对随机参数先验信息的改造,其改造程度由观测值的方差和观测值与参数的相关程度共同决定[6].

本文以Bursa 模型为例研究顾及2 套坐标误差的三维坐标转换, 用2 套坐标改正数的加权平方和最小为准则导出了转换参数的计算公式;并根据公共点的坐标改正数以及公共点与转换点的协方差阵,推估转换点的坐标改正数并对其改正, 从而求得近似无缝的坐标转换结果.采用模拟数据分析了新方法的有效性, 与直接将非公共点转换到新坐标系的传统方法相比, 新方法能有效地提高坐标转换精度.

1 七参数坐标转换模型

Bursa-Wolf 模型以坐标原点为旋转和尺度的参考点,对应的7 个参数转换模型为

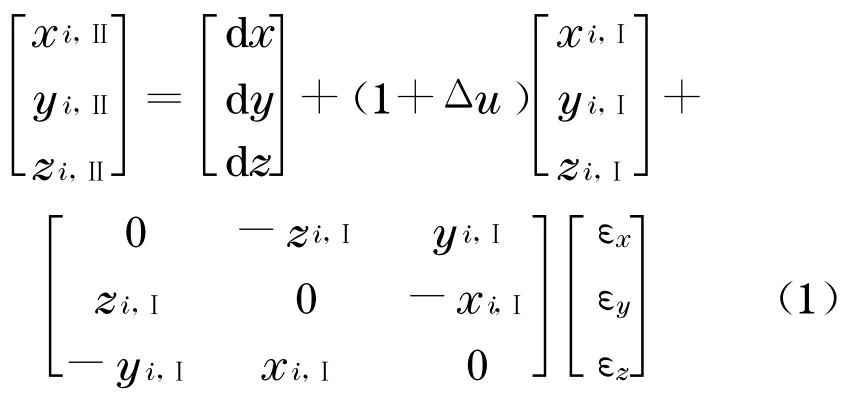
式中:dx,dy,dz为3 个平移参数;εx,εy,εz为3 个旋转参数;Δu为尺度参数;下标Ⅰ与Ⅱ表示2 套坐标系;i表示第i个公共点.假设n个公共点在2 套坐标系下对应的协方差阵分别为Σ11,Ⅰ和Σ11,Ⅱ, 传统的求解方法只考虑公共点在第1 套坐标系下的误差,对应的转换参数的最小二乘解为

2 顾及2 套坐标误差的坐标转换模型

观测向量L 等于第2 套坐标系公共点的坐标向量LⅡ与对应第1 套坐标系坐标向量LⅠ之差,即

采用最小二乘求解,同时考虑观测向量L 中公共点在2 套坐标系下的误差.令vⅡ, vⅠ分别为LⅡ,LⅠ的改正数向量,有

误差方程式可表示为

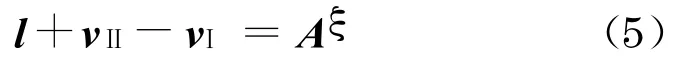
显然, 观测向量LⅡ与LⅠ相互独立, 以2 套公共点坐标改正数的加权平方和最小为准则

根据拉格朗日条件极值原理,构造极值函数

式中:K为联系数向量, ξ为7 参数向量, 分别对残差向量vⅠ, vⅡ和7 参数向量ξ求一阶导数, 并令其为零, 得

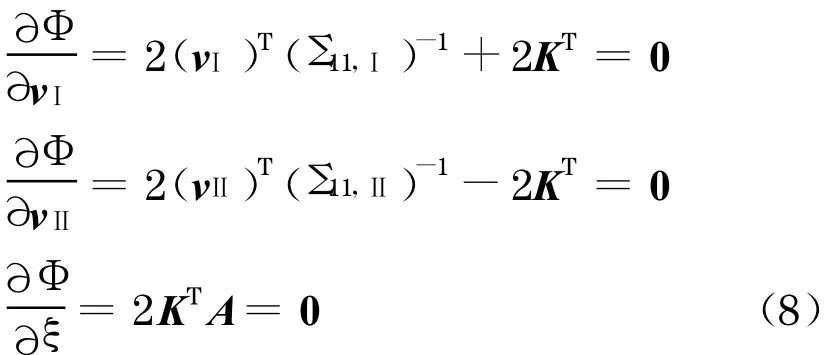
由式(8)中前2 式得

两式相减, 得

顾及式(4)和式(5), 则

将式(11)代入式(8)中第3 式, 得

因此, 考虑二套坐标误差,对应的转换参数的最小二乘解ξ^N为

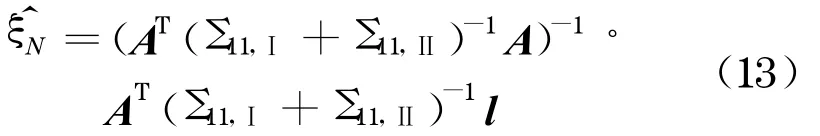
求得转换参数后, 由式(10)计算K,再代入式(9)计算观测值改正数.

3 转换点的坐标改正数算法

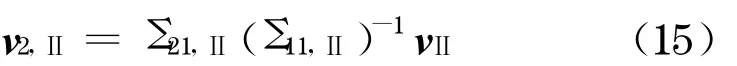
4 算例与分析

4.1 算例设计和协方差的构造

算例旨在验证本文坐标转换方法能否提高坐标转换精度.在经度110°～130°、纬度20°～40°范围内设计2 个方案.方案1 :每隔4°取一个点, 共6 ×6 个点,见图1a ;方案2 :每隔2°取一个点, 共11 ×11 个点,见图1b .

图1 选点方案Fig .1 Point distribution in different control networks

根据图1 中各点的经纬度,设其大地高为0 m ,采用WGS84 椭球参数计算每个点的空间三维坐标作为近似坐标.

在2 种方案中, 第1 套坐标系中的所有点的协方差阵根据三维空间距离观测值的间接平差计算得到,测距精度模拟为10-2+10-8D,D是2 点之间的三维空间距离, 以米为单位.列出点位坐标的估值与观测值L 的改正数v 之间的函数关系为

其中,B 为误差方程的系数阵.则X 的估值协因数阵为

其中,Nbb=BTPB ,P 为权阵.协方差阵为

第2 套坐标系中全部点的协方差阵用GPS 网平差的方式计算.首先根据模拟点坐标计算出任意2点的基线, 给基线模拟标准差为10-2+10-8D的正态分布随机误差, 然后列误差方程式并附加全部点坐标改正数平方和最小为约束条件, 以位于选点范围中部的公共点为基准点进行平差计算, 其中, 3 个基线分量的权取P x=(Δx)2/D2,P y=(Δy)2/D2,P z=(Δz)2/D2.

4 .2 解算与分析

方案1 :根据4 .1 所述, 对图1a 中的所有36 个点分别按照距离观测和按GPS 网平差观测进行,对应得到全部点在第1 套和第2 套坐标系下的协方差阵.平差后考虑网中与外围点相联的观测数较少,点位误差远大于内部点位误差, 如果对全部点位误差统计, 则统计结果不能客观反映内部点位精度,故仅取16 个中间点比较,其中5 个是公共点、11 个是转换点.将5 个公共点按式(13)计算坐标转换参数后,按式(9)计算第1 套坐标系和第2 套坐标系中公共点的坐标改正数vⅠ, vⅡ,再分别用式(14)和(15)计算第1 套坐标系和第2 套坐标系中11 个转换点的坐标改正数v2Ⅰ, v2Ⅱ, 并改正这些转换点坐标(记改正后的第1 套和第2 套转换点坐标分别为～X2,Ⅰ和～X2,Ⅱ);然后用转换参数ξ转换改正后的第1 套转换点坐标～X2,Ⅰ(记为～X2,Ⅱ),并与改正后的第2 套转换点坐标～X2,Ⅱ比较,按式(19)计算11 个转换点的坐标精度

以及按(20)计算转换的点位精度

该过程称为LSC 法.传统方法直接用式(1)计算转换参数ξ^L并转换11 个转换点, 并与X2,Ⅱ比较按式(19)和式(20)计算转换精度, 该过程称为LS 法.为了在统计意义上评价LSC 方法的优越性,按4 .1 中的协方差模拟过程计算1 000 次,并按式(20)分别计算LSC 和LS 坐标转换点位精度,如图2 所示.显然,LSC 的精度比LS 高.类似于方案1 的实验过程, 对方案2 作1 000 次计算,结果如图3 所示.

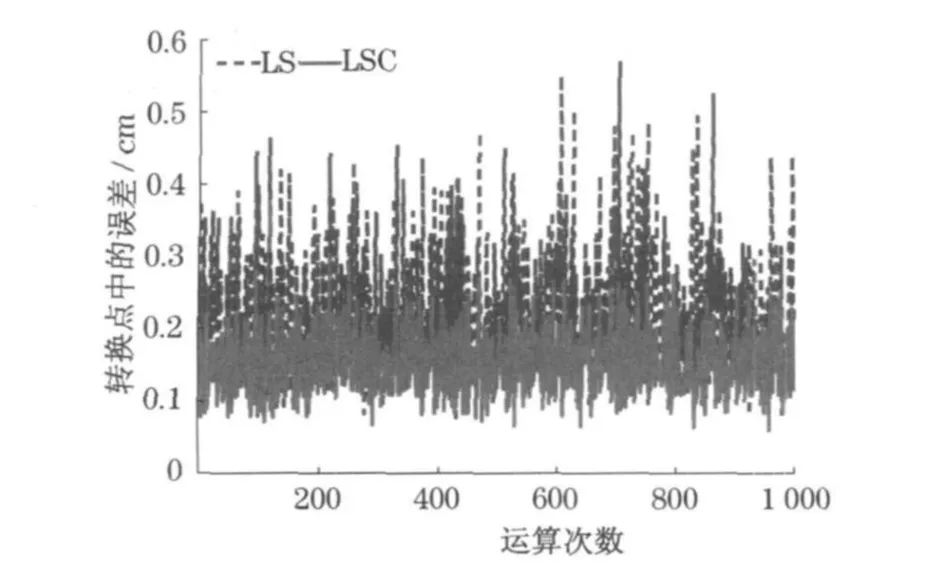
图2 6×6 网中LSC 法与直接转换的误差比较Fig .2 Comparison of errors between LSC method and the direct conversion method for a 6×6 grid

图3 11×11 网LSC 法与直接转换的误差比较Fig .3 Comparison of errors between the LSC method and thedirect conversion method for a 11×11 grid

对2 种方案的1 000 次试验坐标转换点位精度和3 个坐标分量精度统计如表1 所示.表2 给出了精度提高百分比.结果表明:同一范围方案1 选36个点,方案2 选121 个点,当控制点不变, 其余点的点位间距越小, 点与点之间坐标相关性越大, 考虑坐标改正的LSC 方法较LS 方法能有效提高坐标转换精度.

表1 2 种方案的转换精度比较Tab.1 Comparison of conversion accuracy in the two schemes cm

表2 LSC 相对于LS 的精度提高率Tab.2 Rate of increased relativeaccuracy of LSC to LS

5 结论

研究了顾及2 套坐标误差的三维坐标转换模型,以2 套坐标改正数的加权平方和最小为准则导出了转换参数的计算公式;用推估方法根据公共点与转换点的协方差阵计算转换点的坐标改正数并对其改正,求得了无缝的坐标转换结果.得到结论:

(1)坐标转换的2 期坐标通常来自不同测量手段,若已知其协方差阵, 用LSC 法先对转换点坐标修正再进行坐标转换能有效提高转换精度.

(2)当点的坐标之间相关性较大, 直接将转换点的坐标换算成新坐标会产生较大的误差, 采用LSC 法改正,能很好地解决残差问题.

(3)采用本文模型求解转换参数并用LSC 对转换点改正, 能实现整体、无缝的坐标转换结果.

[1] 刘大杰, 施一民, 过静珺.全球定位系统(GPS)的原理与数据处理[M] .上海:同济大学出版社, 1996.LI U Dajie,SH I Yimin, GUO Jingjun.The theory and data processing of global position system (GPS)[M] .Shanghai :Tongji University Press, 1996.

[2] Krarup T .Acontribution to the mathematical foundation of phy sical geodesy [R] . C openhagen : Danish Geodetic Institude,1969.

[3] Mo ritz H .Least squares collocation[M] .Munich:Deutsche Geodaetische Kommission(DGK), 1973.

[4] 周江文.拟合推估新解——两步解法[J] .测绘学报, 2002, 31(2):189.ZHO U Jiangw en.Atwo-step solution of collocation[J] .Acta Geodaetica et Cartographica Sinica,2002, 31(2):189.

[5] 杨元喜, 张菊清, 张亮.基于方差分量估计的拟合推估及其在GIS 误差纠正的应用[J] .测绘学报, 2008, 37(1):152.YANG Yuanxi, ZH ANG Juqing,ZHANG Liang .Estimation based collocation and its in GIS error variance fitting component application[J] .Acta Geodaetica et Cartographica Sinica,2008, 37(1):152.

[6] 李博峰.混合整数GNSS 随机模型及函数模型参数估计理论与方法[D] .上海:同济大学, 2010.LI Bofeng .Theory and method of parameter estimation for GNSS stochastic and function models[D] .Shanghai:Tongji University,2010.

[7] Schaffrin B .T LS-collocation:The total least-squares approach to EIV-models with prior information [C/ CD] ∥18th International Workshop on Matrices and Statistics.Smolenice Castle :Institute of Measurement Science, 2009.