曲率模态及其在汽车后桥损伤识别中的应用

马立英,周 鋐,彭晓俊

(同济大学 汽车学院, 上海201804)

随着汽车结构不断复杂、开发时间不断缩减,车辆在使用过程中出现局部损伤的概率大大提高, 这些局部损伤虽然不会立刻导致整个车辆结构的破坏,但它对整个结构的安全形成了潜在的危险, 由于应力集中、疲劳等诸多因素的影响会使局部损伤不断扩展和增大, 使整个结构的承载能力下降, 从而导致整个结构的破坏.汽车结构件损伤的准确识别将有利于整车结构安全的预防和早期修复.

在众多的模态分析理论中曲率模态是一个能反映局部特征变化的模态参数, 它可以通过各阶振型来得到,且对局部结构的敏感性大大高于振型,所以在结构的状态监测中具有良好的应用前景[1].

本文在曲率模态理论分析基础上, 以某轿车后桥为研究对象, 通过实测模态试验数据用于曲率模态分析和损伤指标计算,对裂纹位置和损伤程度进行识别,从而验证曲率模态在汽车后桥损伤识别应用中的可行性和有效性.

1 曲率模态方法

1 .1 曲率模态理论[2-3]

承弯结构中性层的曲率v为

式中:M为弯矩;E I表示弯曲刚度,E为弹性模量,I为截面的惯性矩.从式(1)可见,结构损伤造成的弯曲刚度下降直接引起结构曲率的变化.通过模态分析,可直接得到结构的位移x模态y.设模态方程为

对位移模态进行中心差分得到曲率模态式(3):

1 .2 汽车结构件曲率模态计算

汽车底盘结构件一般为小阻尼结构, 系统的动力学方程表示如下:

式中:K 为刚度矩阵;Φ为模态振型矩阵;M为质量矩阵;Λ为对角频率矩阵.

假设损伤引起系统中1 个或几个单元的刚度损失,则损伤结构的刚度矩阵、模态频率和模态振型为

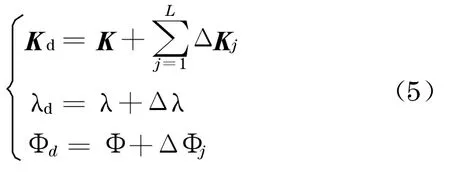
式中:下标d表示受损;j为测点位序;L为系统中划分单元的总数;λ为频率比.通过计算模态或试验模态分析得到模态振型, 对归一化后的振型使用差分近似法计算模态振型的1 阶导数和2 阶导数

式中:φ为位移模态振型;i为振型阶次;x为测点坐标.相应曲率模态k ji可表示为

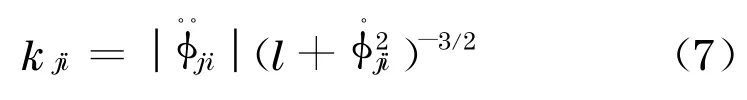
将式(6)代入式(7)可得每个测点的振型曲率模态.

1.3 损伤指标——平均曲率模态绝对差

目前常用的损伤指标有3 种:振型曲率模态、振型曲率模态比和平均曲率模态绝对差[4].

为了选取一个适合本文的基于曲率模态的损伤识别指标,进行了一维梁结构有限元仿真.分析结果表明,上述3 个指标随模态阶数的上升,其对损伤的敏感度变差,特别是4 阶以后.其中,曲率模态对比例为10 %以下的损伤识别困难;曲率模态比虽然可以识别10 %的小损伤,但3 阶、4 阶误差严重;只有平均曲率模态绝对差不仅对损伤程度敏感(见图1),而且损伤单元附近节点的曲率模态峰值变化即使在10%损伤情况下依然明显(见图2),便于顺利识别损伤位置[5].因此本文选择平均曲率模态绝对差作为损伤识别指标.

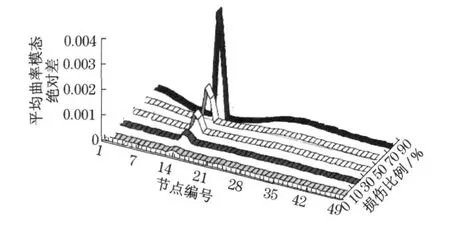
图1 平均曲率模态绝对差Fig .1 Absolute mean difference in curvature mode

图2 10%损伤比例情况下的平均曲率模态绝对差Fig .2 Absolute mean difference at 10% damage

2 试验验证

对某轿车后桥进行模态试验, 将获得的试验数据通过计算平均曲率模态绝对差进行结构损伤的曲率模态识别, 模态分析和损伤识别结果用于验证该方法的有效性和可行性.

2 .1 模态试验

模态试验测量分析系统如图3 所示.

图3 模态试验测量分析系统Fig .3 Modal testing system

试验后桥有2 个,无损试件和损伤试件各1 只,两试件测点布置相同.将后桥分为A,B 两面, 测点分为Aa,Ab ,Ba,Bb 四组.各组有测点21 个,编号位置如图4 .对损伤后桥,其裂纹位置有2 个,第1 个裂纹位于测点Bb17 和Bb18 之间,第2 个裂纹位于测点Ab4 和Ab5之间,而且第2 裂纹长度大于第1 裂纹.

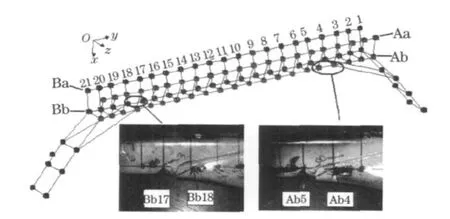
图4 测点布置及裂纹位置Fig.4 Measurement points distribution and crack locations

被测后桥用橡皮绳悬吊安装, 采用多点激振多点拾振的方法在垂向和纵向2 个方向同时激振.

2 .2 模态分析

基于试验获得各测点加速度对2 个激励点的频响函数,利用最小二乘复指数频域估计法原理[6],通过MA T LAB 编程作出试验模态分析稳态图(见图5).

根据稳态图极点的稳定程度选出8 个极点, 其频率、阻尼比及模态参与因子等见表1 .

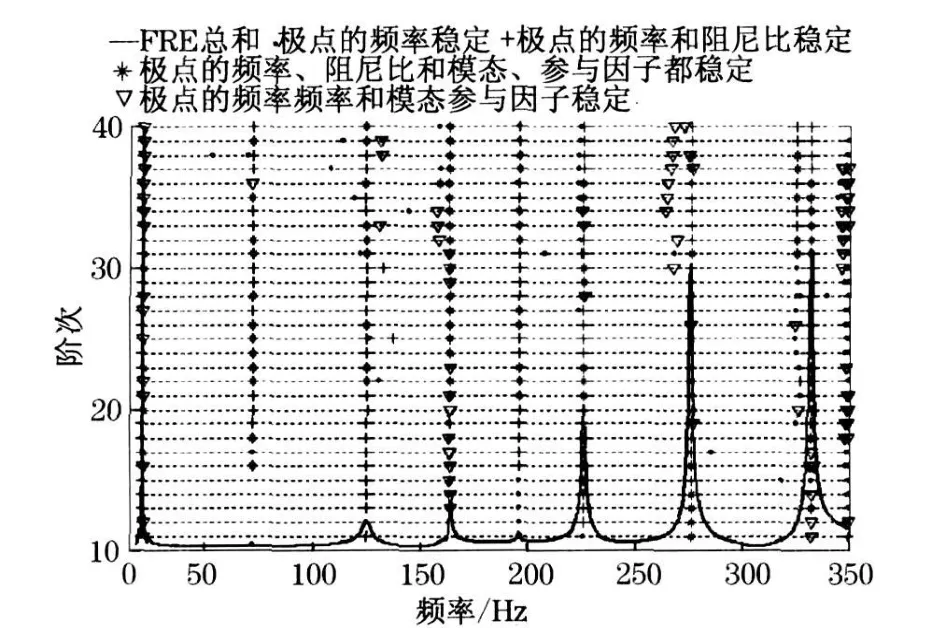
图5 后桥试验模态分析的稳态Fig .5 Stabilization diagram of experimental modal analysis

对选择的极点再次进行最小二乘计算即可求解出系统振型,得到各测点模态振型.

在模态振型基础上计算出模态置信准则Modal Assurance Criterion 值检查有无相似的模态振型,最后通过频响函数(FRF)重构以检查估计模态振型的正确性.重构频响函数的累加与原试验测得频响函数的累加比较见图6,通过比较发现二者相似程度较高、一致性较好,说明试验模态分析估计得到的模态参数正确,可以用于下一步损伤识别.

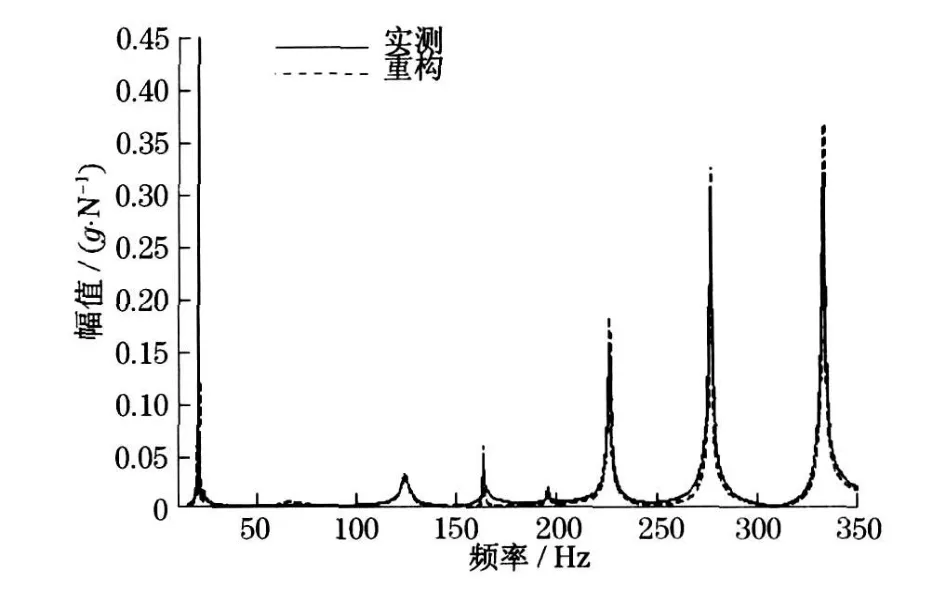
图6 重构频响函数累加和原频响函数累加的比较Fig .6 Comparison between reconstructed frequency response function and frequency response function from modal test

2.3 验证分析

2.3.1 结构损伤与结构刚度关系验证

提取无损后桥与受损后桥x向和z向第1 阶和第2 阶弯曲振型,见表2 .

表2 无损和受损后桥弯曲振型比较Tab.2 Comparison of bending modal shape between the damaged and the undamaged rear axles

由表2 可见, 受损后桥的固有频率低于无损后桥,说明结构损伤造成了结构刚度降低,与曲率模态理论相符合.

2.3.2 损伤识别验证

计算Aa1～21,Ab1～21,Ba1～21 和Bb1～21的振型数据(提取前4 阶)用曲率模态方法,计算损伤识别指标,即平均曲率模态绝对差值.结果见图7 .

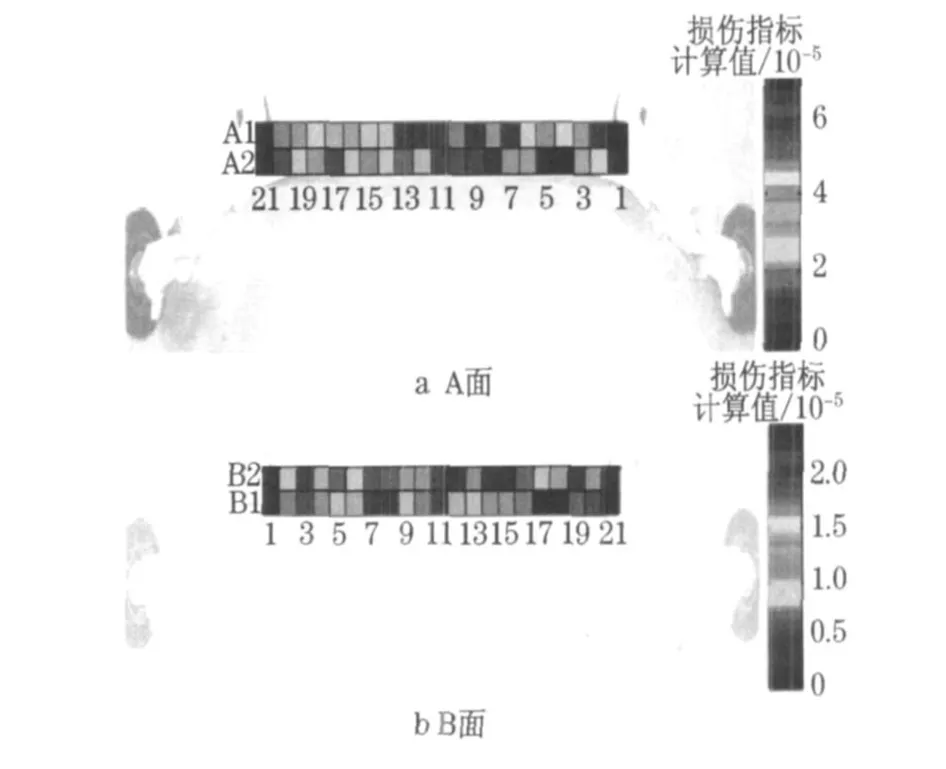
图7 轿车后桥A 和B 面损伤识别结果Fig .7 Results of damage identification on section A and B of rear axle

从图7 后桥A 面中可以看到,节点Ab4 ,Ab5 处损伤指标出现峰值, 与前面所提第2 裂纹位置相符;后桥B 面中,节点Bb17 ,Bb18 处的损伤指标出现峰值,与第1 裂纹位置相符.另外从图中还可以发现,节点Ab4,Ab5 处损伤指标出现的峰值要高于Bb17 ,Bb18 处, 而后桥实际损伤情况是第2 裂纹长度大于第1 裂纹, 两者是相符合的.此外, 从代表损伤指标大小的色块颜色深浅情况可以看出节点Aa16～19 受到了其背面Bb 第1 裂纹的影响,节点Ba4～06 受到了Ab 面第2 裂纹的影响, 因此这些节点上的损伤指标出现了相对较大的值.

通过上述基于曲率模态分析的损伤识别, 后桥上2 处损伤位置以及损伤的相对大小都得到了确定,汽车后桥的损伤识别得以实现.

3 结论

(1)平均曲率模态绝对差不仅识别效果好, 而且由于其对所有阶次曲率模态的变化情况进行了平均,因此有利于消除试验模态分析中噪声带来的影响.

(2)通过无损后桥和有损后桥曲率模态分析,验证了结构受损对结构刚度的影响,与理论相符,应用于汽车结构件模式识别具有一定的可行性.

(3)通过与实际受损后桥裂纹位置和裂纹长度的对比,平均曲率模态绝对差峰值位置与实际损伤位置吻合;其值的相对大小与实际裂纹长度符合.

综上所述, 模态试验结合曲率模态用于汽车后桥损伤识别可行有效.为今后车辆结构件损伤识别提供了一种可行的研究方法.

[1] 叶黔元, 翟立祥, 陈锦辉.曲率模态及其在桁架桥梁伤识别中的应用[J] .力学季刊, 2005, 26(2):286.YE Qianyuan, ZH AI Lixiang,C HE N Jinhui.Application of curvature mode shape in damage identification of truss bridge[J] .Chinese Quarterly Mechanics, 2005,26(2):286.

[2] Wahab MMA,Roeck G D .Damage detection in bridges using modal curvatures:application to a real damage scenario [J] .Journal of Sound and Vibration, 1999, 266(2):217.

[3] 郑明刚, 刘天雄, 朱继梅, 等.曲率模态在桥梁状态监测中的应用[J] .振动与冲击, 2000, 19(2):81.ZH ENG Minggang,LIU Tianxiong,ZH U Jimei, et al .Bridge diagnosis using curvature mode shapes[J] .Journal of Vibration and Shock,2000, 19(2):81.

[4] 刘蕾蕾.基于曲率模态分析的桥梁损伤识别研究[D] .成都:西南交通大学, 2007.LI U Leilei.Research of damage Identification of bridge based on curvature modal analysis[D] .Chengdu:Southwest Jiaotong University,2007.

[5] 彭晓俊.模态分析在车辆结构件损伤识别中的应用[D] .上海:同济大学汽车学院, 2010.PENG Xiaojun.Application of modal analysis in damage identification of automobile structural components [D] .Shang hai: T ongji University . College of Automotive Studies, 2010.

[6] Verboven P,Cauberg he B,Parloo E,et al.User-assisting tools for a fast frequency-domain modal parameter estimation method[J] .Mechanical Sy stems and Signal Processing,2004, 18:759.