钻孔千斤顶压裂测量技术的发展和原地测量*
2011-12-19YokoyamaOgawaSanoHirataMizuta
Yokoyama T,Ogawa K,Sano O,Hirata A,Mizuta Y
1)OYO Corporation,Saitama,Japan
2)The University of Tokyo,Tokyo,Japan
3)Sojo University,Kumamoto,Japan
钻孔千斤顶压裂测量技术的发展和原地测量*
Yokoyama T1),Ogawa K1),Sano O2),Hirata A3),Mizuta Y3)
1)OYO Corporation,Saitama,Japan
2)The University of Tokyo,Tokyo,Japan
3)Sojo University,Kumamoto,Japan
为了测量距地表1 000m以下位置的地壳应力状态,我们研究并开发了钻孔千斤顶压裂技术。技术的原理是:当钻孔千斤顶对钻孔壁加载时,与钻孔轴向平行的方向将会产生两个相对的新裂隙;卸载之后,如果千斤顶对钻孔壁的同一个地方进行施压,这对裂隙将会再次张开。与钻孔轴向垂直的平面上的两个主应力的大小和方向分别是由重张压力和裂隙的方向决定的。这个技术与水压致裂法相似。因此,测量深度没有理论上的限制。这个技术的特点就是它可以产生一对任意方向的轴向裂隙,可以测量裂隙张开的位移大小,根据测量结果可以精确计算重张压力的大小。在实地测试中,先用水压致裂法形成裂隙,再用钻孔压力千斤顶法加以与水压近似相等的压力值使之重张。本文介绍了我们的数值分析结果、实验室实验和现场测试。
引言
在地球科学领域,我们需要深度超过1 000m的广大区域内的应力分布来决定震中区周边的地应力。另一方面,在岩土工程建设中,人们需要建筑物周围深度在1 000m以内的初始应力分布。当然,这两种应用都需要高精度的测量。不管怎样,在地震预报中,水平方向上的二维应力分布对地应力的评估仍然非常重要。三维应力分布的资料对可靠的地下结构设计极其重要,即使这些资料局限于狭窄的有限区域中。
在工程和地球科学领域,人们提出了多种应力测量的方法。地球物理研究杂志专集中的世界应力图(World Stress Map,WMS)收集了1992年之前全世界的地应力测量数据[1]。Zoback[1]之后,应力测量主要通过以下几种途径获取:震源机制解(54%),钻孔崩落(28%),断层滑动(5.5%),水压致裂(4.5%),火山序列(4.1%)和应力解除法(3.4%)。这些方法中,震源机制解给我们提供了主应力的方向和与地震相关的应力变化。断层滑动和火山序列只能给我们提供主应力的方向。这些数据并不包含任何与应力值大小相关的信息。与钻孔相关的钻孔崩落法给我们提供了应力的大小和方向。应力解除法和水压致裂法被认为能够更加准确地测量主应力的方向和大小,但是这两种方法所占的比例却出乎意料地低。应力解除法更多地应用于深度小于50m的范围内,而在更深的深度上水压致裂法的应用占主导。但是,除了崩落法以外没有其他方法能为我们提供深度大于3km的资料。这些通过钻孔的测量方法相当有用,因为它们能提供主应力的大小,而这点是其他方法做不到的。
应力-应变关系的非线性、各向异性和不均匀性几乎是所有岩石共同的特征。由于现在的应力分析方程都是基于均匀的各向同性的弹性体,因此如果测试岩石的性质跟理想的岩石相差很大,其最终的计算结果就会有很大的误差。这是一个能够直接影响计算结果准确性的非常重要的问题。同样,现在应力解除技术适用的深度为距离地表50m或更浅。这个问题与测量技术相关,所以需要发展新技术,诸如开发能提供更高水压的设备技术、能在深钻孔中安装设备的技术和用绳索钻孔的套钻技术。
在这些技术中能够解决这些问题的是水压致裂。由于应力解除技术的理论是基于由应力解除所导致的应变的测量,因此需要将应变换算为应力。另一方面,水压致裂方法基于力的平衡原理能够直接测量地应力。但是,这种方法有两个关键的问题到现在都没有得到完全解决[2-3]:
(1)如果裂隙重张时水压影响到其内部;
(2)如果从非线性的压力-时间曲线拐点上计算出的压力并不是重张压力而是闭合压力。
这些疑问不仅仅提出了关于测量准确性的问题,同样也提出了关于水压致裂法基本方程本身一个非常重要的问题。这个问题基于用液体作为液压介质这样一个基本原理。尽管使用的是低塑性或高刚性的系统,但当主应力的比值大于3时得到的重张压力也是没有用的。目前,我们采用钻孔千斤顶压裂方法来克服这些问题[4]。
1 钻孔千斤顶压裂技术
钻孔千斤顶压裂技术的原理是使用金属盘来给钻孔壁施加压力,观测重张垂直裂隙和钻孔壁周围应力分布之间的关系。它与水压致裂技术相似。这种技术的优点在于我们可以在需要的方向上构建垂直裂隙,通过使用位移应变仪能够准确地测量裂隙的重张行为。这种技术能够消除使用水作为压力源所产生的问题。另一方面,由于水压并不影响裂隙的内部,因此我们需要更高的压力系统来扩展裂隙。
人们提出这种技术是为了通过钻孔千斤顶在钻孔壁上形成垂向的裂隙来确定岩石的杨氏模量[5-6]。这种技术能提供最大水平应力SH、最小水平应力Sh和主应力方向。不过,这种技术具有这样一种缺陷,就是由于压力壳和钻孔壁之间曲率的微小差异所导致的其他方向的裂隙。图1为钻孔千斤顶机制的概要原理图[7]。图1指示了独特的压力盘和压力壳,这样的装置能够克服上面所提到的缺陷。施加于钻孔壁上的压力是通过带有锯齿的特殊的压力壳传导而不是直接与固体压力盘相接触。裂隙张开的宽度使用位于钻孔壁表面上的位移传感器来直接进行测量并通过观测窗口进行观测。图2是钻孔千斤顶压裂探测仪的照片。
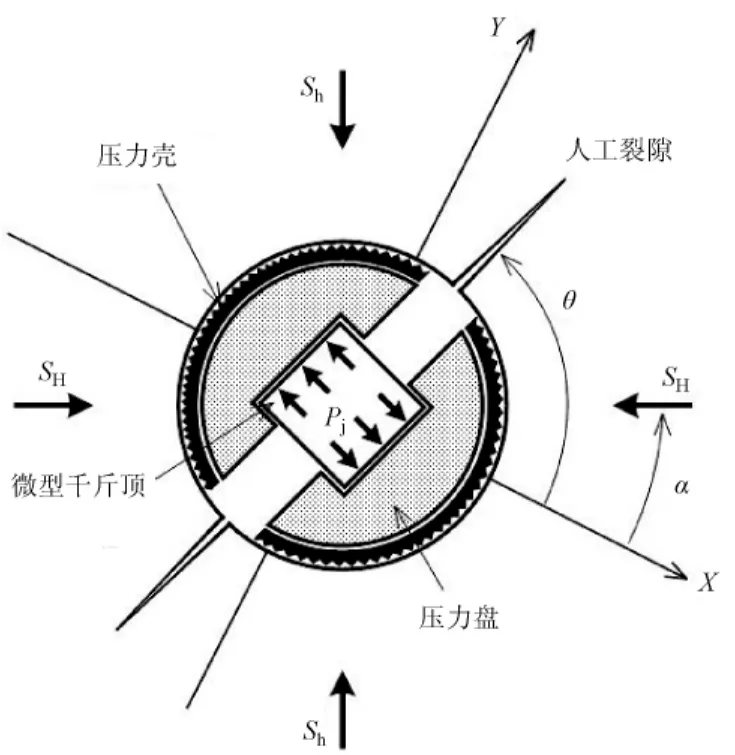
图1 钻孔千斤顶压裂探测仪的原理简图[7]。能在任意3个方向形成破裂并且能测量重张压力。两个主应力及其方向未知

图2 钻孔千斤顶压裂探测仪的原型。(a)探测仪整体;(b)探测仪头部;(c)中间部分和变位仪。压力盘和压力壳之间的间隙能使压力壳和钻孔壁很好地接触
采用这种技术,当压力壳开始向钻孔壁施压以及切向应力达到零的时候裂隙将会重张。裂隙重张的条件可以用以下方程来说明:

其中,k为探测仪设计的灵敏系数;Pj为液压千斤顶的压力;Sh为最小水平应力;SH为最大水平应力;θ为给定坐标中裂隙的方向;α为给定坐标中主应力的方向;P0为裂隙周边的孔隙压力。
SH、Sh和α都是未知的。但是,如果我们获得至少3个方向上的裂隙张开的Pj值,那么方程就能求出以上未知解。由于裂隙能在任何方向产生,所以钻孔千斤顶压裂技术的优势就在于即使主应力比率大于3的情况下方程也能适用。同时由于设备能张开同一个裂隙,所以方程还可用于测量旋转主应力的大小。
2 数值分析
如果裂隙能在预期方向形成,我们就可以进行数值分析。分析代码为FLAC。表1列出了主要条件。分析模型是假定是轴向对称的均匀各向同性弹性体。它是一个中心有着98mm直径孔洞的正方形模型。它具有一个自由活动端(在部分实例中是固定的)并处于平面应变状态(部分实例中是平面应力状态)。图3给出了分析结果的一个实例。
探测仪和岩石之间的耦合条件会影响方程(1)中的灵敏系数k。图4给出了灵敏系数k与压力壳和钻孔壁耦合条件之间关系的分析结果。纵坐标是灵敏系数,横坐标是从压力壳中心开始的耦合区域的角度。在壳顶端耦合区域的角度为24°,39°,45°,60°,70°,80°和81°。

表1 数值分析的假设

图3 分析结果的一个实例。在水平应变和自由端的条件下张应变集中在压力盘的开口边缘

图4 数值分析得出的灵敏系数k与耦合区域角度之间的关系
图4表明,当耦合区域的角度小于60°时,灵敏系数k几乎不发生变化。这意味着当耦合区域角度小于60°时,即使和预期的耦合区域有微小的差别也不会严重影响到灵敏系数k。相应地,这也表明了评估重张压力的可靠性。这个结果表明即使在和初始破裂具有不同的接触区域条件下所进行的重张压力测量也将是一种有效的方法。
图5指出了从数值分析中提取的钻孔壁内(距离钻孔壁表面为2mm)切向应变的分布。在这个实例中,压力壳耦合区域角度为45°,60°,75°和80°。耦合区域越宽张应变就越大。实际探测仪中,由于张应变更多的是集中在张开的边缘区域,因此当耦合区域更大或张开的边缘间隙更少时,灵敏系数将会变大并且使破裂更容易发生。

图5 从数值分析(图3)得出的切向应变分布。张开边缘应变较狭小,耦合区域变大应变增强
切向应变几乎是一个常数,当耦合区域的角度达到±30°的时候其最大值为44×10-6。另一方面,张开的空隙区域的应变值为168×10-6是切向应变的3.8倍。正如前面所解释的,如果耦合区域的角度小于60°,在张开区域的张应变近似为100×10-6。但是,随着耦合区域的增大张应变形成两个峰值。我们认为造成这种现象的原因是耦合区域边缘的应力集中所致。这些都是距离钻孔壁表面2mm处的应变量。但是432×10-6这个尖锐的峰值可以在张开区域的钻孔壁表面观测到,因此,我们认为新的裂隙从这一点开始产生。
3 实验室实验
我们可以用数值分析确定压力壳、耦合系数和切向应变分布之间的关系。然后我们用钻孔千斤顶探测仪在一个模型钻孔壁上施压,来研究钻孔壁周边应变的分布。以下是这次实验的3个目的:
(1)验证压力壳和钻孔之间直径的差异对于应变分布的影响;
(2)验证灵敏系数;
(3)观测应变在破裂和重张瞬间的发展。
本次实验所用的岩石样品是中间含有钻孔的600mm×600mm×64mm的细粒辉长岩样品。我们准备了3个钻孔直径分别为96.7mm(小),97.2mm(中)和97.7mm(大)的样品。钻孔千斤顶直径为97.2mm,我们期望能观测到在不同的压力壳和钻孔壁接触条件下的应变分布的差异。
为这次实验我们准备了新的探测仪,与图2所示的有所差异。探测仪总长120mm并带有长86mm,直径97.2mm的压力传感器。图6即是这种名为“微型千斤顶”的实验设备。微型千斤顶与钻孔壁接触区域的角度为81°。由于使用3个活塞的汽缸而提高了效率,微型千斤顶施压的能力是图2所示的原型探测仪的2.3倍。图7是安装在岩石样品钻孔上的微型千斤顶。图8给出了岩石样品上应变测量仪的位置。应变仪的有效长度为5mm。

图6 实验室实验用的微型千斤顶。(a)微型千斤顶的整体;(b)微型千斤顶的零部件

图7 微型千斤顶和装有应变仪的岩石样品

图8 应变仪的方位。它们安装在切向和径向方向。少数也安装在岩石样品其他部位
3.1 压力壳与钻孔之间直径的差异对应变分布的影响
图9是直径为96.7mm(小)的钻孔直径切向应变的分布。由于采用96.7mm直径的钻孔,在张开的边缘区域可以观测到显著的张应变峰值(200×10-6~250×10-6)。由于钻孔直径比压力壳小0.5mm,压力壳边缘和钻孔壁之间的受力接触使得边缘区域具有很大的张应变。

图9 微型千斤顶对钻孔大小为96.7mm(小)的岩石样品加载得出的切向应变分布的典型例子
在钻孔直径为97.2mm(中)的情形下,相比于压力壳中心较小的张应变(10×10-6~20×10-6),我们在边缘区域能够观测到相对较大的张应变(100×10-6~140×10-6)。这种测试条件与前面解释的数值分析模型是非常接近的,其数值结果和变化趋势相比其他条件更接近于数值模型分析的结果。然而,我们没有观测到从数值模型分析得出的在压力壳边缘应变集中的两个峰值。这个结果甚至更接近于96.7mm钻孔(小)的数值模型。当应力在边缘集中的时候,这两个峰值应该会出现。我们假定采用97.2mm(中)钻孔模型其边缘的接触稍弱。
在钻孔直径为97.7mm(大)的情况下,我们可以观测到压力壳区域中心的压应变(-3×10-6~85×10-6)和张开边缘周围广阔区域(稍小于90°)内为常量的张应变(近似为100×10-6)。中心区域的压力高于边缘的原因是由于钻孔的最大孔径比压力壳还稍大,钻孔变形成了椭圆状。从这个现象,我们认识到,钻孔和压力壳之间直径的细微差异对于灵敏系数有很大的影响。
3.2 验证灵敏系数
灵敏系数对评估裂隙的重张压力相当重要,必须通过实验来确定。由于灵敏系数对压力壳和钻孔壁的接触极其敏感,因此不能仅通过数值分析来求得。为了实验性地得到灵敏系数,我们用微型千斤顶对相同的岩石样品做了载荷试验,对钻孔轴的横切方向施加恒定的单轴载荷。从对钻孔表面开始加载单轴载荷到解除载荷,我们观测切向应变在孔壁表面的转变,从而得到灵敏系数。初始加载单轴载荷的时候,加载方向上的切向应变对钻孔壁是压缩的。当微型千斤顶加载到一定压力后,切向应变变为零。灵敏系数k从下式得到:

其中,Pj是液压千斤顶的内部压力,σθ0是钻孔壁表面的切向应变。
图10是本次实验所用的单轴加载设备。该设备包含两个10t的液压千斤顶。应变将通过安装在钻孔壁表面中心两侧垂向上的应变仪进行测量,应变仪如图8所示。
灵敏系数通过以下步骤确定。首先,液压千斤顶提供的单轴压力是3.5MPa,钻孔壁表面的垂向应力必须是单轴应力的3倍,因此,σθ0=10.5MPa。其次,当切向应变达到0时,微型千斤顶的压力是15.0MPa。相应的灵敏系数为k=σθ0/Pj=10.5/15.0=0.7。最后,微型千斤顶的有效长度是75mm,而测试件的厚度仅为64mm,因此补偿灵敏系数为0.7×64/75=0.6。

图10 岩石样品安装在单轴加载设备中。微型千斤顶将从上往下加载
3.3 观测应变在破裂和裂隙重张瞬间的变化
3.3.1 无加载情况下裂隙形成和裂隙重张我们通过应变仪观测了由微型千斤顶加载形成的初始裂隙和裂隙的重张。图11是初始裂隙和裂隙重张现象,是图7无单轴加载试验的解释结果。这个结果是在图9所示的“96.7mm(小)模型”张应力峰值处(10 ch)测量的。应力-应变曲线的拐点对应微型千斤顶大约17MPa的压力。如果我们将灵敏系数0.6考虑在内(17MPa×0.6),这就意味着大约10.2MPa的张应力发生在钻孔壁的表面。因为岩石的抗张强度在10.2MPa附近,我们推断这是张裂隙。我们能直观地证实实际破裂瞬间。破裂瞬间应变现象最重要的方面是裂隙附近(9ch,8ch)的切向应变开始压缩张应变变小。这种现象看上去好像是当应力超过岩石样品强度时,在破裂瞬间横切裂隙的张应变释放的结果。
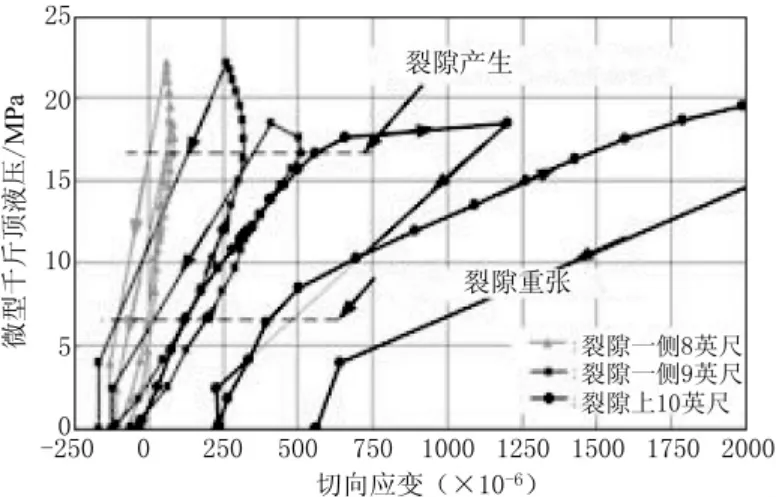
图11 裂隙产生和重张时压力和应变的关系。无单轴载荷时钻孔壁裂隙周边切向应变分布现象
接着,第二次通过微型千斤顶液压加载,应力-应变曲线在7MPa附近有急剧的拐点。我们认为这是裂隙重张压力。如果没有施加单轴载荷,当微型千斤顶开始加载时裂隙就应该立即重新张开。但是,我们认为初始裂隙的端点到达距离表面一定深度处,并且要到达更深处需要加载更大的压力。
3.3.2 单轴加载条件下裂隙重张和灵敏系数的关系
我们实施单轴加载条件下裂隙重张测试的目的是为了验证灵敏度和微型千斤顶重张压力之间的关系。对于这次测试,我们在小的裂隙发生之后横切裂隙安装了应变计来确定重张开时的应变。由于施加于岩石样品上的单轴应力是已知的,我们计划验证通过先前实验中的灵敏系数值0.6计算出的重张压力是否能够由应变的变化来确定,其中将单轴应力作为一个参数。
表2给出了单轴应力、由单轴应力计算出的切向应力和由灵敏系数计算出的微型千斤顶压力之间的关系。图12给出了微型千斤顶压力和横切裂隙并沿切线方向安装的两个应变仪测出的张应变之间的关系。表2给出单轴加载条件下的6个不同阶段。在图12中,箭头表示从表2中的灵敏系数计算出的重张压力。每个曲线中的拐点都不是很清楚,但我们可以在期望的压力周围识别出它们。
4 原地实验
为了验证钻孔千斤顶的现场测试,我们在现场实施了由水压致裂引起的裂隙重张试验。测试地点位于神冈矿Atotsugawa入口北北东方向1.1km。距离Atotsugawa断层1km,距地表0.6km。钻孔打在从Atotsugawa隧道向西开凿的地下隧道中。钻孔深20m,直径98mm。

表2 单轴应力条件下,切向应力σθ0和微型千斤顶压力Pj之间的关系

图12 考虑灵敏系数评估重张压力。破裂现象是通过横切裂隙安装在岩石样品两侧的两个应变仪测量的
在12m深钻孔上采用水压致裂,接下来对钻芯样品进行检查以及对钻孔壁内表面的视觉观察以确保没有天然裂隙存在。水压致裂之前我们采用了压印器测试来铸造钻孔壁表面。随后进行了几次裂隙重张测试。表3是水压致裂反复测试的结果。
水压致裂形成裂隙之后,我们用图2所示的钻孔千斤顶探测仪来进行裂隙重张测试。正如之前所描述的那样,如果探测仪的压力壳和钻孔壁耦合区域的角度小于±60°,灵敏系数将保持稳定。图13是安装之前钻孔千斤顶探测仪的照片。位于探测仪中部的名为“TSS”的位移测量仪用来测量横切裂隙的两点之间的位移。“TSS”测量横切裂隙的位移。

表3 水压致裂实验结果

图13 Kamioka矿Atotsu隧道中地应力测量地点。图片右下角是一幅用钻孔千斤顶探测仪在钻孔壁加载的照片
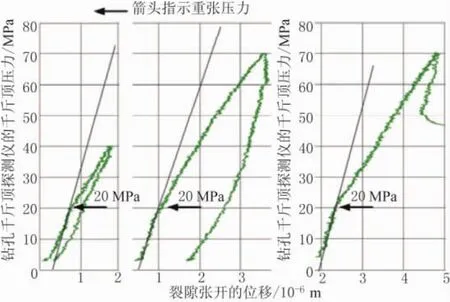
图14 用钻孔千斤顶使裂隙重张时裂隙张开的位移和钻孔千斤顶压力之间的关系。这些裂隙在表3水压致裂中就已经形成。周期载荷曲线指出了拐点为20MPa,这就确定了重张压力的大小
图14是通过钻孔千斤顶压裂探测仪获得的一些结果,这些曲线代表钻孔千斤顶压力和横切裂隙的位移之间的关系。在这3个曲线中,拐点都在20MPa附近。将这些拐点处的压力值确定为裂隙重张时的千斤顶压力Pj。对于这个测试,探测仪的灵敏系数k计算为0.45×0.56=0.25。其中,0.45是图4所示的接触区域角度小于±60°的平均灵敏系数,0.56是千斤顶圆柱体的有效横截面。与此相应,重张压力计算结果为20 MPa×0.25=5.0MPa。
现在,水压致裂技术的方程如下所示:
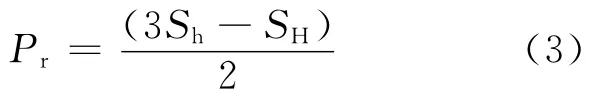
其中,Pr为重张压力,Sh为最小水平压应力,SH为最大水平压应力。
方程(3)中的Pr是用水压致裂测得的重张压力。同一裂隙在钻孔千斤顶破裂作用下重张压力相当于(3Sh-SH)。这意味着钻孔千斤顶破裂确定的重张压力是水压致裂测得的Pr的2倍。即钻孔千斤顶破裂确定的5.0 MPa重张压力相当于水压致裂的Pr=2.5 MPa。在这里我们再来回顾一下表3,重张压力在2.05~2.39MPa附近,这些都与钻孔千斤顶破裂产生的重张压力Pr=2.5MPa很接近。
5 结论
像开始介绍的那样,如果二维平面上的主应力的比率大于3的话,不可能用水压致裂方法来评估地应力。我们一直致力于钻孔千斤顶压裂技术的改进以期能解决这个问题。钻孔千斤顶压裂方法的一个重要方面就是能准确测量裂隙重张压力以及钻孔壁的切向应力。下面将分别介绍数值分析的结果、实验室和原地的测试以及剩余的工作。
5.1 数值分析
在数值分析中,将压力壳沿切线方向长度的变化作为一个参数,目的是为了证实压力壳的影响。进行数值分析是在假定压力壳与钻孔壁是紧密耦合,它们之间没有滑动条件下进行的。灵敏系数表明压力千斤顶形成裂隙的效率,其值近似为0.45并且只要刚性耦合区域方向与加载轴向夹角小于60°时将保持不变。当耦合区域的角度大于60°时,灵敏系数将会大大增加。当耦合区域的角度为80°时,灵敏系数为0.68。因此,沿切向方向更长的压力壳将会更有效地形成裂隙,而较短的压力壳只有在求解重张压力上显得较为方便。
5.2 实验室实验
实验室模拟模型的应变分布实验表明,当压力壳直径比钻孔壁直径大1.3mm时将会更有效地形成裂隙。为了确定新设计的微型千斤顶的灵敏系数,我们用液压千斤顶对试样中的一个钻孔做了恒定单轴加载测试。从施加在微型千斤顶上的压力和微型千斤顶开口附近的切向应变的关系我们得出灵敏系数k=0.6。
第一次破裂的发生以及它们的重张都可以通过从这次加载测试的压力-应变曲线上的拐点来确定。同样,我们实施裂隙重张测试的目的是为了确定单轴加载下重张压力和灵敏系数之间的关系。从逐步单轴加载所计算出的重张压力和压力-应变曲线之间的关系证实了微型千斤顶灵敏系数的相关性。
5.3 原地实验
我们在水压致裂形成的裂隙上实施了图2所示的新设计的钻孔千斤顶裂隙重张测试。钻孔千斤顶压力壳和钻孔壁的刚性耦合区域角度控制在60°以确保恒定的灵敏系数。结果证实,钻孔千斤顶重张压力几乎与水压致裂相同。该试验结果支持Ito等[2]所描述的机制。
译自:Proceedings of the 5thInternational Symposium on In-Situ Rock Stress“Rock Stress and Earthquake”,Edited by Furen Xie,CRC Press/Balkema,Leiden,The Netherlands:93-100,2010
原题:Development of borehole-jack fracturing technique and in situ measurements
(中国地震局地壳应力研究所研究生 徐 伟译;中国地震局地质研究所研究生 张 雷,中国地震局地壳应力研究所研究生 姚 瑞,中国地震局地壳应力研究所研究生 沙 鹏 校)
(译者电子邮箱,徐伟:xwazhy@163.com)
[1]Zoback M L.First-and second-order patterns of stress in the lithosphere:the world stress map project.J.Geophys.Res.,1992,97:11 703-11 728
[2]Ito T,Evans K,Kawai K,et al.Hydraulic fracture reopening pressure and the estimation of maximum horizontal stress.Int.J.Rock Mech.Min.Sci.Geomech.Abstr.1999,36:811-826
[3]Ito T,Igarashi A,Ito H,et al.Problem for the maximum stress estimation by hydrofracturing method and its potential solution.Proc.US Rock Mech.Symp.,Anchorage:ARMA/USRMS 05-862(CDROM),2005
[4]Mizuta Y,Sano O,Ishida T,et al.A prototypal probe newly developed for stress measurement in the Earth’s crust.Chikyu Monthly.2004,26(2):97-102(in Japanese)
[5]De la Cruz R V.Jack fracturing technique of stress measurement.Rock Mech.,1977,9:27-42
[6]Yokoyama T,Nakanishi A.A proposal of geostress measurement technique by plate fracturing.Proc.Int.Symp.Rock Stress,Kumamoto,1997:143-148
[7]Sano O,Ito H,Hirata A,et al.Review of methods of measuring stress and its variations.Bull.Earthq.Res.Inst.Univ.Tokyo.,2005,80:87-103
P315.7;
A;
10.3969/j.issn.0235-4975.2011.01.011
2010-11-15。
