注入系统压缩性和粘性流体流动对水压致裂破碎压力影响的模拟＊

Bunger A P，Lakirouhani A，Detournay E

1）CSIRO Earth Science and Resource Engineering，Melbourne，Australia

2）Zanjan University，Zanjan，Iran

3）University of Minnesota，Minneapolis，MN，USA

注入系统压缩性和粘性流体流动对水压致裂破碎压力影响的模拟＊

Bunger A P1），Lakirouhani A2），Detournay E3）

1）CSIRO Earth Science and Resource Engineering，Melbourne，Australia

2）Zanjan University，Zanjan，Iran

3）University of Minnesota，Minneapolis，MN，USA

基于水压致裂数据估计岩体的最大应力主要取决于对破裂的确定和二次破裂压力。这种估计的误差可归结于注入系统压缩性，耦合粘性流体在水压裂隙中的流动和裂隙通过井孔周围变化的应力场的增长。这些机制的作用还没有很好的定量化。本文中的两个数值模型为评估非理想条件下与破裂压力分析有关的误差提供了一个基本工具。这两个数值模型是注入系统的压缩性和各向异性的岩石应力场中粘性流体在从井孔扩展的水压裂隙中的流动。为了保证足够的精确性，结果对于相关的无量纲参数值采用基于模型的标准，当这些标准在现场条件下满足不了时，模型可以进一步应用获得一级校正，来解释压缩性、粘度和近井孔的影响。

引言

广泛应用垂直井孔的水压致裂方法来确定地应力[1－4]。最小水平应力σh由水压裂隙在闭合或返流条件下结束时井孔压力的估计值确定。普遍认为用水压致裂法能更精确确定应力分量。另一方面，测定最大水平应力σH需要重新打开已存在的不同方向的裂隙，即HTPF试验[5]，或者，当HTPF不能实际应用时，就需要分析破碎和／或重张压力。后者有许多的不确定性，对地应力估算来说，经常认为对破裂压力的分析是不可靠的。

分析非渗透性岩石中破裂压力Pb的两个经典方程是Hubbert和Willis（H－W）[6]

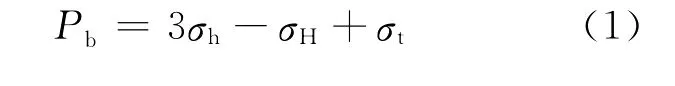
及Haimson和Fairhurst（H－F）[7]

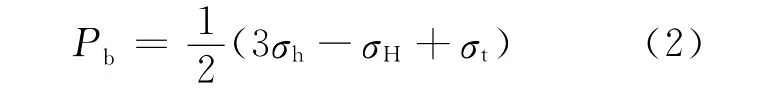
其中σt是抗拉强度。

第一个明显的不确定性是，H－W准则和H－F准则的差异因子是2，这可以通过从裂隙开始增长时的有限长度裂隙的引入得到解决[8－10]。H－W准则和H－F准则分别代表两个极端情况：快速增压（无流体渗透）和缓慢增压（完全渗透和均匀分布的裂隙）。从井孔扩展的有限裂隙的引入使得基于准则的抗拉强度隐含的信息明朗化了：裂隙存在于物质中。本文我们延伸了这项工作，考虑到水压裂隙是从一个来自充满液体井孔的小裂隙增长而形成的，此时应力正好大于最小地应力σh。用两个模型模拟水压裂隙的增长，即用注入系统的压缩性和粘性流体流动来追踪水压裂隙的增长。

可用相同的方法来分析注入和闭合的多周期特点，因为每个新的注入和新的裂隙长度相对应。在这种情况下，出现的问题是，破裂能否在后来的注入阶段观测到，并且观测到的破裂压力的意义是什么。此外，在实际操作中，将重张压力Pr定义为钻孔压力在压力－时间记录曲线变成非线性时的大小，对Pr的有关解释也一直是众多争论的主题。Bredehoeft等[11]提出，用σt＝0时方程（1）作为重张准则（假设σH＜3σh，因为在注入开始之前裂隙已经张开）。另一方面，Ito等[12]认为σt＝0时方程（2）是适合的准则，因为裂隙在关闭时有残留的缝隙，假如注入速度足够小的话，这就使得裂隙在重新张开之前不均匀受压。然而，低于注入速率临界值时方程（2）（σt＝0）是相关的重张准则，关于该值的依赖性还没有充分研究。最后，就像Ito等人[12]指出的那样，重张压力受到注入系统液压屈服度的影响。

最终目标是阐明关于解释破裂压力Pb的另外一个重要的不确定性，Pb一般比裂隙增长开始时的压力Pi要大。Detournay和Carbonell[13]预测，Pb≥Pi建立在对极限平衡曲线的分析上，对平面应变裂隙来说，曲线本质上就是应力强度的变化。该预测被Zhao等人[14]通过试验所证实，他们的结果和预测是一致的：当σH＝σh时，Pb＝Pi；当σH＞σh时，Pb＞Pi。Ito等人[15]也预测Pb＞Pi，原因是注入系统的压缩性。Lakirouhani等[16]指出第3个因素是压缩系统和粘性流体流动的耦合。虽然认为所有这些机制都起着作用，但是这些影响还都没有定量化。因此，为了定量化近井孔应力场、注入系统压缩性和粘性流体流动对破裂和重张压力的作用，本文运用Lakirouhani等[17]给出的算法来模拟水压裂隙初始和破裂状态。

1 数学模型

1.1 问题描述和主要方程

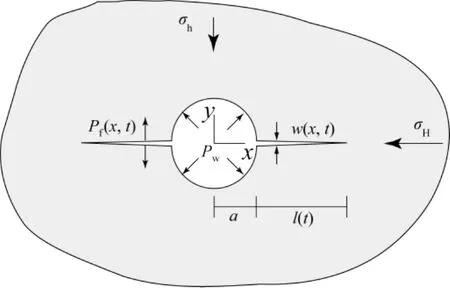
图1 示意图

在非渗透线弹性岩石中两个对称破裂面的平面应变半径为a的井孔传播受以下几个量影响：杨氏模量E、泊松比ν和破裂韧度KIc（图1）。因为是对称的，方程只需求右边破裂，即a≤x≤l（t）＋a，破裂长度为l（t）。解决这个问题必须确定l（t），张开w（x，t），流体压力分布Pf（x，t）和流体流量q（x，t）。这些量在如下方程中：

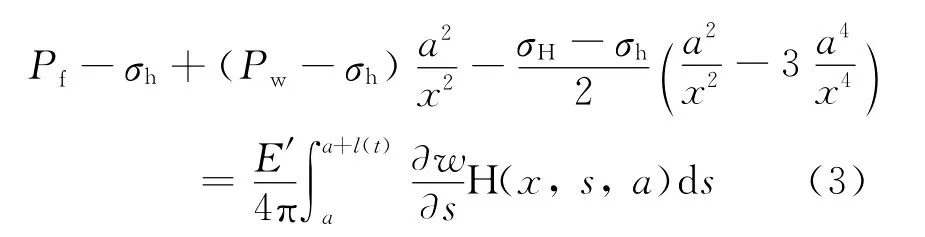
其中，弹性核心函数H（x，s，a）隐含井孔[18]。E′＝E／（1－ν2）是平面应变弹性系数，Pw（t）＝Pf（0，t）是井孔的流体压力。

考虑到裂隙中不可压缩的牛顿流体的层流，流量q可通过泊肃叶方程给出：

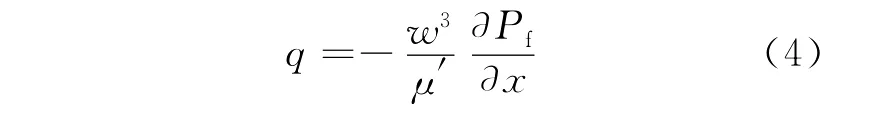
其中，μ′＝12μ是动态粘滞度。需要注意的是，注入系统是可压缩的，但是我们认为流体的压缩性对方程（4）和以下连续方程是可忽略的：

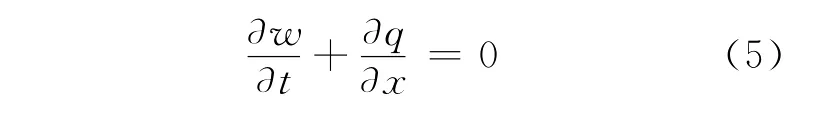
第四，我们需要一个移动边界方程调整l（t），在KI＝KIc条件下从线弹性破裂机制（linear elastic fracture mechanics，LEFM）给出，其中，KI是模式I的应力强度，KIc是模式I的破裂韧度。LEFM传播条件可由下式表达：

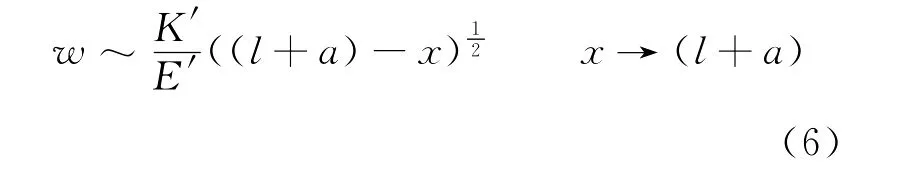
两个边界条件在裂隙尾端张开和流体流量条件下给出：

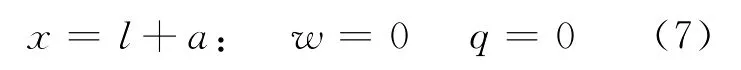
第3个边界条件是，考虑到注入系统的压缩性，进入裂隙的流体流量和钻孔压力变化速率之间的线性关系如下：

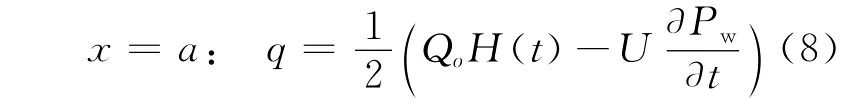
其中，H（t）是Heaviside单位阶跃函数。这里我们看到，注入的净流体（沿井孔坐标轴单位裂隙的高度）是以一个常数Qo注入的液体减去储存在可压缩的注入系统的那部分U∂Pw／∂t，其中U是沿井孔坐标轴单位裂隙的高度注入系统的体积缩小。如果大部分注入系统压缩性都归为液体体积的压缩，那么U≈CfVo，其中Cf是液体压缩系数，Vo是沿井孔坐标轴单位裂隙高度注入系统的体积。初始条件为：

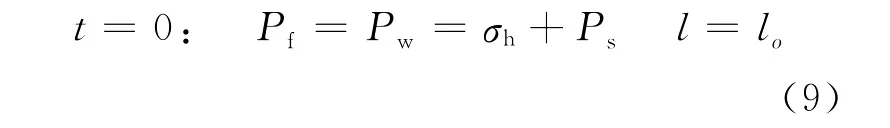
其中，Ps是一个小的初始净压力，假设最初就存在于裂隙中。这在算法上是必需的，因为解答必须以一些小的初始张开开始。在物理上，相对于最小应力σh来说，这是一个小小的过压，假设它已经存在了很长时间并且已经渗透到了最初的裂隙中。

1.2 比例法

控制方程的无量纲形式的比例法的应用可以减少参数空间的量纲，只考虑无量纲参数。如果Ps足够小，不影响结果的话，我们有3个独立的量（即，力、长度和时间）和10个独立的变量（x，t，a，U，K′，μ′，E′，σd，σh，lo）。因此，我们需要最多考虑7个独立的无量纲参数[19]。这里，为了方便数值解法，我们选择了特殊比例。特别是，我们寻找了一个有固定空间坐标的尺度，作为相对于移动或拉伸的坐标系。最后，如果这个比例能对结果的解释有一些最直观的帮助是最好的。

令L为一个特征长度，即γ＝l／L是一个无量纲长度。我们选它作为破裂体积Vcrack，类似于储存在注入系统的液体的体积Vcomp。对于具有均匀净压力Pw－σh的裂隙，Vcrack～（Pw－σh）L2／E′。正如1.1部分讨论的那样，Vcomp＝（Pw－σh）U。因此得出下式：

另外，由于系统的线性特征，特征长度可以理解为裂隙压缩性和注入系统类似时裂隙的长度。可以得出在注入速率为Qo时，达到特征长度的时间：

如果裂隙中的压力接近Pw－σh，LEFM预测，加上初始及边界条件：

其中：

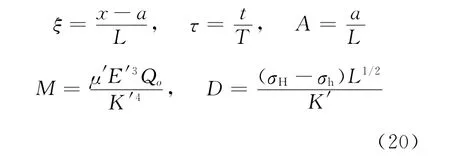
注意，下面的计算中初始条件是初始压力Πs＝0.01。

因此，｛γ，Π，Ω，Ψ｝是ξ，τ，A，M，D和γo的函数。当γ和τ很小时，l＜＜L，因此压缩性的影响很大。当γ和τ趋向无限大时，压缩性的影响消失。参数D包含了偏应力，当γ和τ趋向无限大时该量随时间减小并消失。参数M是个无量纲粘度，通过裂隙传播决定粘性流动。最后，A是井孔半径和特征长度L之比。因此，A＜＜1⇔a＜＜L，井孔半径比特征裂隙长度小很多。也就是，对于A＜＜1，注入系统的影响是持续的，直到接近井孔的应力集中可以忽略。

1.3 数值解

数值解是通过基于位移不连续（displacement discontinuity，DD）算法离散化弹性方程和基于有限差方法解出润滑方程计算得出的[20]。算法运用离散单元尺寸为△ξ的固定格网，和基于具有相同位移的DD单元。每一步，裂隙的长度相对于最初未知的时间间隔△τ都以一个固定的增量△ξ增加。因此，未知的不是裂隙的长度，而是时间。该方法的优点在于不需要特殊的逻辑去处理单元之间落下的裂隙尖端。

2 水压裂隙初始状态和增长

2.1 裂隙长度和井孔压力的演化

在τ＝0，开始注水，井孔压力增加，流体在传播准则满足之前流进裂隙一段时间，然后传播才开始。图2展示了长度γ和井孔压力Πw随τ的变化。当初始裂隙大小γo较小时，开始之前的注入阶段要持续较长的时间才会使压力增大为较高的值。一旦传播开始，γ快速增大，因为注入系统的体积释放了。图2展示了非粘性流体的数值结果[1617]，与Lhomme等人[21]认为的一分钱形状的裂隙的结果是一致的。当M≡0时，随着γ从较低向较高的数值跳跃，裂隙长度瞬间增长。图2展示了M＝0.001和M＝0.1的情况。当M＝0.001时，γ确实瞬间就增大，而井孔压力却瞬间下降。相反，当M＝0.1时，γ的增长就缓慢多了，井孔压力的下降也是如此。

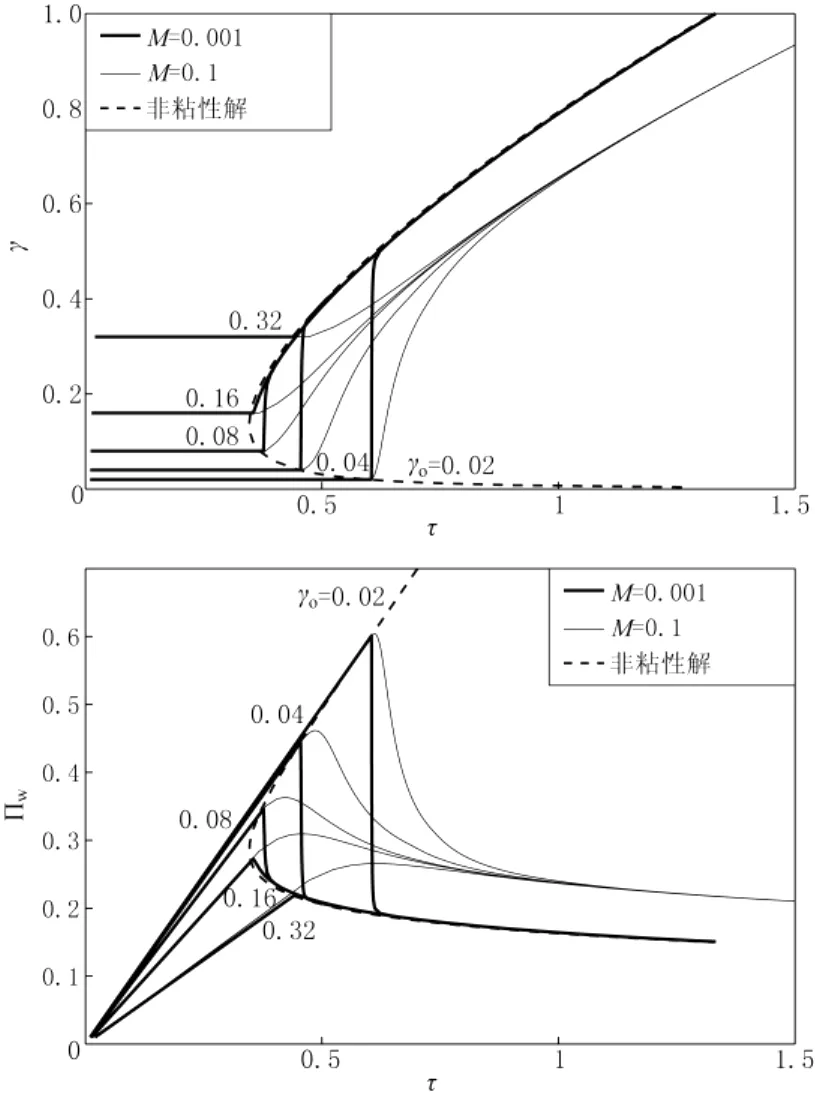
图2 裂隙长度γ（a）和井孔压力Πw（b）曲线。其中D＝0，A＝0.4。虚线是粘度为0的情况[17]

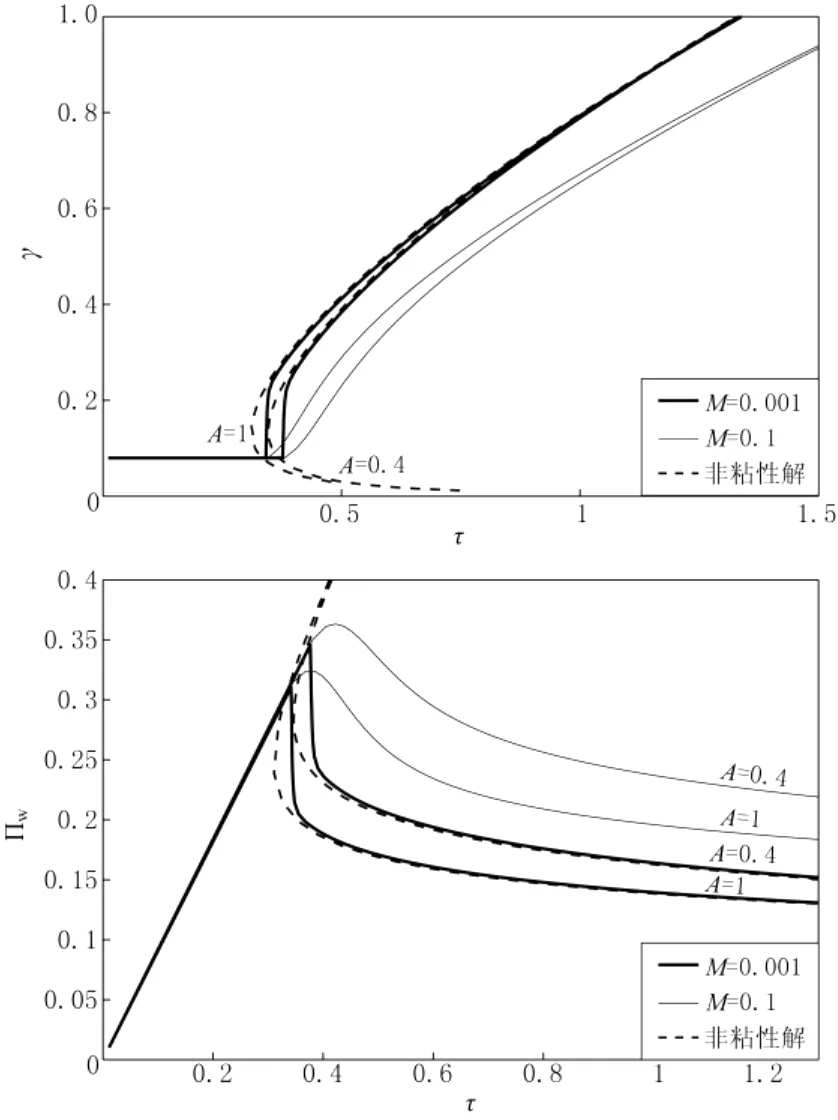
图3 裂隙长度γ（a）和井孔压力Πw（b）在不同井孔半径A条件下随τ的变化曲线。其中D＝0，γo＝0.08，虚线是粘度为0的情况[17]

图3和图4展示了最初增压、裂纹萌生的类似情况，及裂纹长度急速增长的最初趋势，这种增长因粘度M变得缓慢。图中展示了不同井孔半径A和偏应力D对应的结果。很明显，在γo固定的情况下，无论哪个参数值的增大都对减少初始时间和初始井孔压力有影响。

2.2 初始值和破裂压力

以前的预测[13]和实验[14]证实，破裂压力被定义为峰值压力或最大压力，它在裂隙最初增长时能超出最初压力。图2～图4显示最初井孔压力Πi小于破裂井孔压力Πb。差值主要依赖于γo，D和A，当D和A足够小时，差值消失。图5a显示了这种情形，此时粘度为0，M≡0。破裂压力和初始压力差值随初始裂隙长度和压缩性长度的比率γo的变化而变化。解释数据时假设Πi＝Πb，这样产生的误差与γo的中间范围有关。当γo足够大或者足够小时，误差消失。抛开γo的中间值，假设Πi＝Πb时，误差的意义是深远的。因此，从数据解释、注入工具设计和运作协议的角度来说，我们能看到，如果解释要准确的话，必须小心避开那些清晰的参数空间区域。

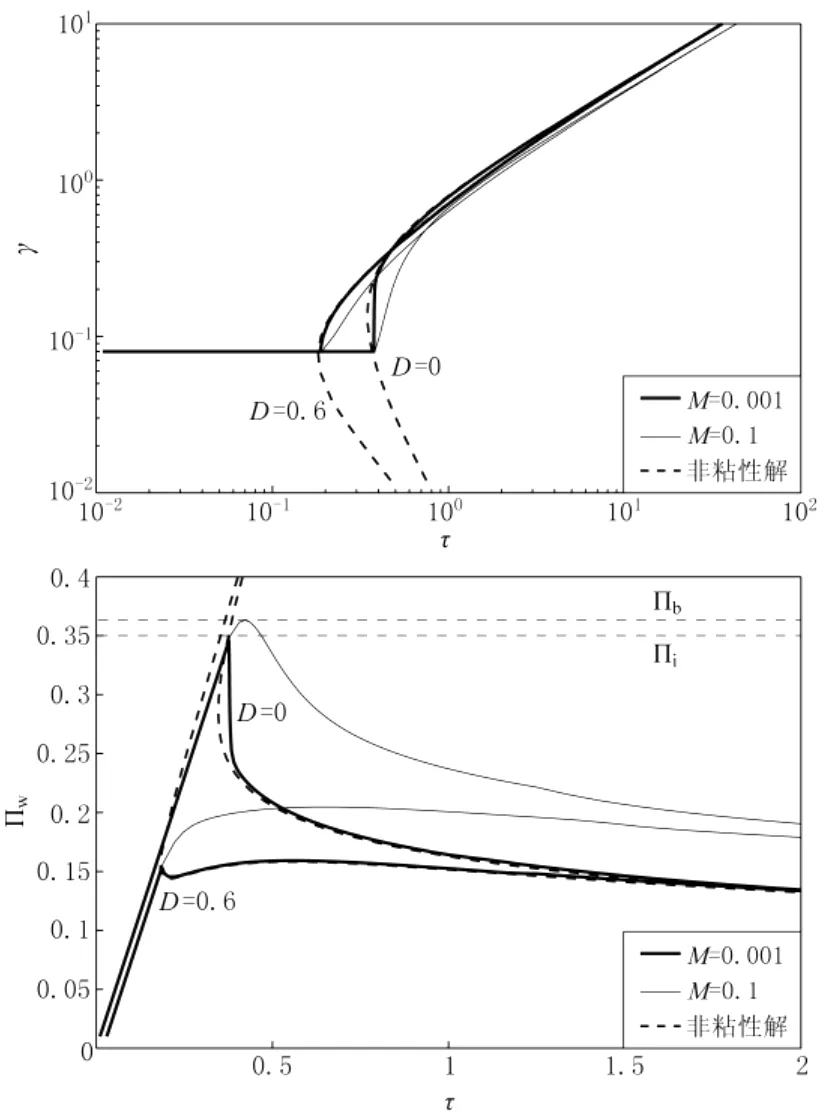
图4 裂隙长度γ（a）和钻孔压力Πw（b）在不同D值情况下随τ的变化曲线，此时A＝0.4，γo＝0.08，虚线是粘度为0的情况[17]

Πi和Πb的差值也随着M增加。图5b阐述了这种相关性。这种影响是双重的：第一，当M＝0时，Πi＝Πb，图5b中只有一个是这种情况，很显然，M＝0.1时，Πi＜Πb。第二，在M＝0，Πi＜Πb的情况下，当M＞0时，差异变大；很显然在γo很大时，差异没有消失。

2.3 二次破裂压力和重张压力

最初注入阶段的破裂压力观测反映出一种情况，即最初的裂隙变得非常不稳定。如果粘度M＜＜1，则裂隙长度从初始值γo很快跳跃到一个新值（图2）。数值解从不稳定到稳定的过渡随着粘度的增加而更缓慢。只要γo比γ＊小，破裂不稳定就会发生（γ＊是临界裂隙长度，非粘性数值解的两支在此合并）。γ＊取决于A和D，数值解的不稳定只是受M微弱地影响。在A＝0.2，0.4时，γ＊随D变化（图6）。

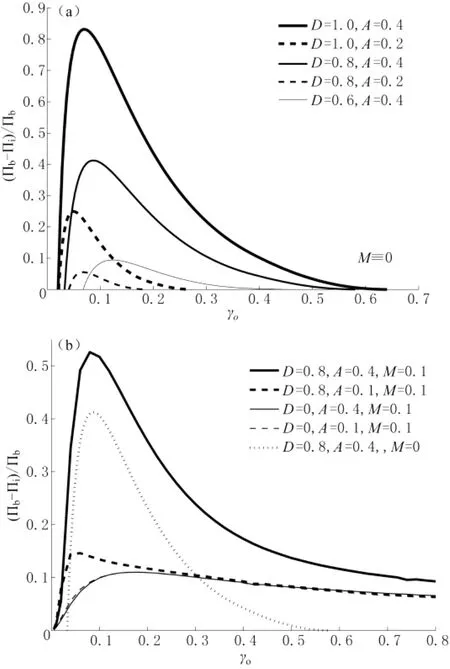
图5 破裂压力Πb和初始井孔压力Πi的差值在不同D和A值条件下随γo的变化曲线。（a）M＝0；（b）M＝0.1

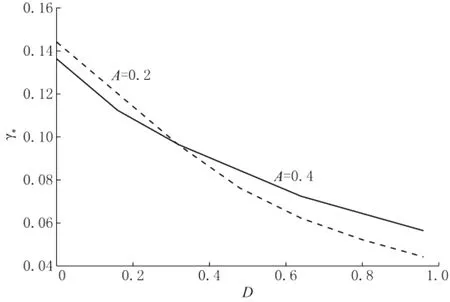
图6 临界裂隙长度γ＊解从稳定向不稳定过渡的曲线

伴随初始注入／闭合周期，任何新的注入都会导致进一步的裂隙传播。一般而言，新的注入是以压力－时间曲线记录上的峰值为特征的。然而，峰值压力有时被称为二次破裂压力，有时被称为重张压力，该概念有不同的含义，用下面的例子来说明。在图2中，γo＝0.08，M＝0.001，A＝0.4。在破裂处，Π⋍0.35。当裂隙快速传播至γ⋍0.25时，压力Πw降至约0.24。假设第一次注入进行到裂隙γ＝0.32时，相应的Πw⋍0.22，此时回流突然产生引起裂隙降压而不是进一步的传播。一旦恢复到平衡（Π⋍0），就开始新的注入。相关的压力－时间记录在Π⋍0.22之前是准线性的，之后裂隙传播重新开始。

两个含义值得进一步检验。第一，例子中观测到的峰值压力与数值解从非稳定支到稳定支的跳跃是无关联的，就像在第一个注入阶段。事实上，从图2可以很明显地看出，压力峰值随着裂隙长度的增长逐渐变得不清楚，这是由于受到随着γ变化的水力屈服增大和净压力传播减小的共同影响。因此，对于第二个注入阶段压力－时间曲线上可轻易辨认的顶点的存在极大地取决于最初增压／减压周期结束时裂隙达到的长度。另外，随着注入系统屈从U的增大，分辨试验压力－时间曲线上的峰值的能力也会进一步减小，因为实际时间轴通过与U3／4成比例的值拉伸了时间τ轴。

第二，模型预测的重张压力将会和闭合压力基本相同。在重张压力的例子中，我们希望最初裂隙长度γo大于破裂长度，我们也希望仅仅是由于最初压力和破裂压力的差异而出现不同，并且当M→0时，差异消失（图5）。闭合压力和重张压力的接近相等是数值解的一个属性，这是由于我们使裂隙重张之后再开始使水压裂隙扩展。重张机制本质上像初始破裂，但是由于岩石已经破裂，韧度或抗拉强度为0[3]。但是，由Sano等[4]提供的大范围的场地试验数据论证了重张压力和闭合压力接近等值，看起来可以支持这里的重张模型。

重张压力有一个重要的应用含义。很显然，σH对裂隙初始和破裂时的影响和近井影响有关，也就是说，在没有井孔条件下，σH和Griffith破裂无关。因此，如果想从重张压力中获得相关信息来决定σH，那么我们的结果表明，在初始注入阶段的末期，裂隙长度没有那么长以致使近井影响消失。也就是说，在二次注入阶段，想要取得σH可靠信息的可能性随着初始注入阶段的延续而减小。而且，较小的初始裂隙长度和稳定传播重新开始时的较大的裂隙长度相符合。因此，当初始注入时，γo非常小，在σH条件下，破译出重张压力的可能性也很小。

3 破裂压力模型的比较

模型结果可以用来估算经典的基于抗拉强度的模型的情况，如方程（1）或（2），预计会对破裂压力给出一个很好的估计。当然，需要有一定的条件，即在现场应用中测量的破裂压力评估希望能产生一个准确的σH。在M≡0和完全渗透性及均匀压力下，流体渗透进初始裂隙。由于传播条件，我们仅限于M≾0.1的情况，因此，比较将会集中在全渗透的H－F准则上[方程（2）]。

首先，抗拉强度σt必须和断裂韧度KIc及初始裂隙长度lo有关[10]。当lo／a＜＜1时，有凹口的井孔可看作边缘裂隙。抗拉强度破裂压力模型把σt假想为裂隙开始增长时作用在非常小的裂隙上的均匀拉张有效应力。因此，从断裂力学观点来看，考虑受到均匀抗拉强度σt的有限裂隙，令KI＝KIc，则破裂传播为

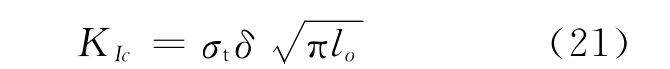
对边缘裂隙[22]，δ＝1.121 5。再联合方程（12），方程（2）变为：

数值模型和方程（22）的H－F准则的潜在分歧的两个源头是很明显的。这涉及到先前讨论的问题，即破裂压力有时可能比初始压力大很多。然而，检查该问题之前，让我们首先考虑由有限裂隙长度lo产生的矛盾。考虑M≡0即零粘度的情况，Pf为常数，并且Pw＝Pf。令P＝Pf－σh，则模型I的应力强度由下式给出[16－17]：

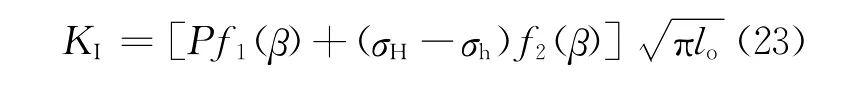
其中β＝lo／a，f1、f2如图7所示。令KI＝KIc，求P，代入方程（12），得出非粘性流体破裂准则：

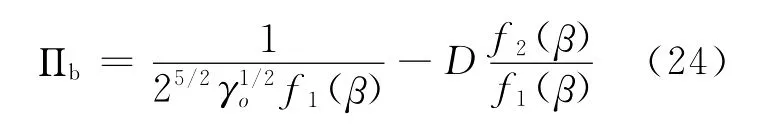
图7 当β＝lo／a时的函数f 1（β）和f 2（β）

检查f1、f2会发现：

因此，方程（24）在β→0时变为方程（22）。当β为有限值时，误差出现了。利用方程（21），β可以由下式估计：

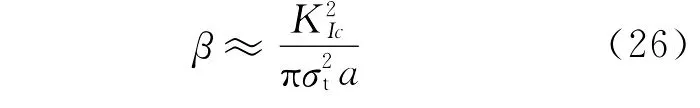
其中δ＝1，因为假设σt是在配置中独立测量得到的。如果实际容差在5%，这和β≾0.02相符合。如果容差放宽到10%，利用抗拉强度标准的准则也放宽到β≾0.05；如果考虑KIc／σt≈1／8 m1／2，那么β≈5 mm／a。因此，有限尺寸的初始裂隙的影响是很重要的，除非井孔半径超过100 mm。实验室内，影响可能是巨大的。Haimson和Fairhurst[23]通过有井套的井孔的增压测量抗拉强度是Brazilian在不同岩石类型中间接测定的结果的1.3～2.4倍，而这种影响可能就是导致以上这种现象的一个原因。因此，无论是在现场还是在实验室，为了能根据方程（24）计算正确的破裂准则，实用的方法是用方程（26）估计β。

利用方程（2）估算σH误差的可能性超出了有限裂隙尺寸的问题。第二个可能的矛盾来自于这样一种事实，即破裂压力经常超出裂隙初始压力（图5）。图8表示在所有情况下，初始压力Πi都非常接近方程（24）。确实是这样，尤其是当M→0时，小误差与尖端条件有关[17]。另一方面，大多数情况下破裂压力显著偏离方程（24）。这种偏离表明方程（24）的应用倾向于显著误差，而显著误差随着M，D和γo的增加而增加。

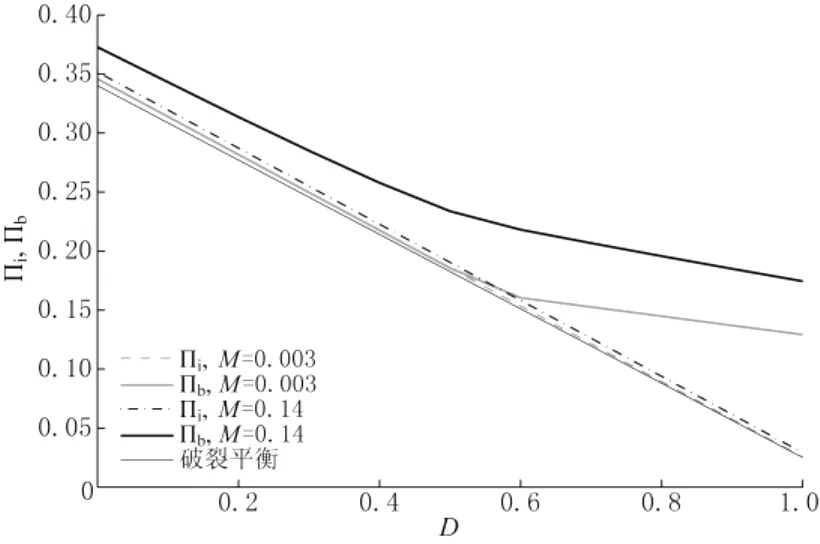
图8 初始压力Πi和破裂压力Πb在不同M值下随D变化，其中γo＝0.08，A＝0.4

4 结论

为了估计最大地应力，采用基于计算水压裂隙破裂压力方程的标准抗拉强度，这依赖于以下两点：一是假设初始裂隙相对于井孔半径来说非常小，二是破裂压力和裂隙初始压力一致。由于场地和实验室条件，这两个假设都可能达不到。在理想情况下，粘性流体流动、注入系统井孔渗透性、近井孔应力影响和初始裂隙长度都可以忽略，测量才能进行。这些机制都确实可以忽略的情况已经由耦合的水压致裂模型Ⅰ阐明。另外，实践中不可能总能获得参数值的合适范围，在非理想情况下进行的应力测试总会带来误差，模型只是一个对这种误差进行定量和纠正的有用工具。最后，也检验了二次注入，如果初始注入阶段持续足够长时间以致于近井孔影响消失时，那么基于所谓的重张压力能可靠地确定σH的能力就减小了。

致谢

感谢Rob Jeffrey和Xi Zhang富有帮助的讨论。AL在对CSIRO访问时开发了数值模型，并作为他博士研究的一部分。非常感谢CSIRO的资金支持。

译自：Proceedings of the 5thInternational Symposium on In－Situ Rock Stress“Rock Stress and Earthquake”，Edited by Furen Xie，CRC Press／Balkema，Leiden，The Netherlands：59－68，2010

原题：Modelling the effect of injection system compressibility and viscous fluid flow on hydraulic fracture breakdown pressure

（中国地震局地壳应力研究所研究生 扈桂让译；徐 伟，姚 瑞 校）

（译者电子邮箱，扈桂让：huguirang＠163.com）

[1] Haimson B，Fairhurst C.In－situ stress determination at great depth by means of hydraulic fracturing.Society of Mining Engineers of AIME.1970，chapter 28，559－584

[2] Zoback M，Haimson B.Status of the hydraulic fracturing method for in－situ stress measurements.In：Proc.23rd U.S.Symp.Rock Mech.，1982，143－156

[3] Haimson B C.Hydraulic fracturing stress measurements，special issue.Int.J.Rock Mech.Min.Sci.＆Geomech.Abstr.1989，26：447－685

[4] Sano O，Ito H，Hirata A，et al.Review of methods of measuring stress and its variations.Bull.Earthq.Res.Inst.Univ.Tokyo.，2005，80：87－103

[5] Cornet F H.Comprehensive Rock Engineering，volume 3，chapter 15：The HTPF and the integrated stress determination methods.1993

[6] Hubbert M，Willis D.Mechanics of hydraulic fracturing.Trans.AIME，1957，210：153－168

[7] Haimson B，Fairhurst C.Initiation and extension of hydraulic fractures in rocks.Soc.Pet.Eng.J.，310－318.SPE 1710，1967

[8] Ito T，Hayashi K.Physical background to the breakdown pressure in hydraulic fracturing tectonic stress measurements.Int.J.Rock Mech.Min.Sci.，1991，28（4）：285－293

[9] Detournay E，Cheng A D.Influence of pressurization rate on the magnitude of thebreakdown pressure.In：Proc.33rd US Rock Mechanics Symposium，325－333.Rotterdam：Balkema，1992

[10] Garagash D，Detournay E.An analysis of the influence of the pressurization rate on the borehole breakdown pressure.Int.J.Solids Struct.，1997，34（24）：3 099－3 118

[11] Bredehoeft J，Wolf R，Keys W，et al.Hydraulic fracturing to determine regional in situ stress filed，in the Piceance Basin，Colorado.Geol.Soc.Amer.Bull.，1976，87：250－258

[12] Ito T，Evans K，Kawai K，et al.Hydraulic fracture reopening pressure and the estimation of maximum horizontal stress.Int.J.Rock Mech.Min.Sci.，1999，36：811－826

[13] Detournay E，Carbonell R.Fracturemechanics analysis of the breakdown process in minifracture or leakoff test.SPE Production ＆Facilities August，1997：195－199.SPE 28076

[14] Zhao Z，Kim H，Haimson B.Hydraulic fracturing initiation in granite.In：M.Aubertin，F.Hassani ＆H.Mitri（eds.），Proc.2nd North American Rock Mechanics Symp.，Montreal，Rotterdam：Balkema，1996，volume 2，1 279－1 284

[15] Ito T，Sato A，Hayashi K.Two methods for hydraulic fracturing stress measurements needless the ambiguous reopening pressure.Int.J.Rock Mech.Min.Sci.，1997，34（3－4）：Paper No.143

[16] Lakirouhani A，Bunger A P，Detournay E.Modeling initiation of hydraulic fractures from a wellbore.In：Proceedings 5thAsian Rock Mechanics Symposium，Tehran，Iran，2008，1 101－1 108

[17] Lakirouhani A，Bunger A P，Detournay E.Modeling initiation and propagation of hydraulic fractures from a wellbore with applications to in situ stress testing.Int.J.Rock Mech.Min.Sci.，2010，To be submitted

[18] Dundurs J，Mura T.Interaction between an edge dislocation and a circular inclusion.J.Mech.Phys.Solids 12.1964，177－189

[19] Barenblatt G.Scaling，Self－Similarity，and Intermediate Asymptotics.volume 14 of Cambridge Texts in Applied Mathematics.Cambridge UK：Cambridge University Press，1996

[20] Crouch S，Starfield A.Boundary Element Methods in Solid Mechanics.London：Unwin Hyman，1983

[21] Lhomme T，Detournay E，Jeffrey R.Effect of fluid compressibility and borehole radius on the propagation of a fluid－driven fracture.In：Proceedings of 11thInternational Conference on Fracture.Turin，Italy，2005

[22] Tada H，Paris P C，Irwin G R.The Stress Analysis of Cracks Handbook.New York：ASME，3rd edition，2000

[23] Haimson B，Fairhurst C.In－situ stress determination at great depth by means of hydraulic fracturing.In：Proceedings of The 11thU.S.Symposium on Rock Mechanics，559－584.Berkeley，CA.，1969

P315.7；

A；

10.3969／j.issn.0235－4975.2011.01.008

2010－11－15。