主成分分析与BP网络组合的大坝变形预报

张建喜， 臧德彦

(东华理工大学测绘工程学院，江西抚州344000)

主成分分析与BP网络组合的大坝变形预报

张建喜， 臧德彦

(东华理工大学测绘工程学院，江西抚州344000)

将主成分分析与BP神经网络相结合应用到大坝变形影响因子的优化中，建立大坝变形预测模型。可以有效地降低输入因子的维数，减小因子之间相关性的影响，简化网络结构，降低网络训练难度，提高预测的稳定性及精度，提升BP网络训练的效率，解决由影响因子内部相关性而需引入大量因子的问题。通过实验结果对比表明，主成分分析与BP网络相结合的大坝预报模型精度及稳定性明显优于其他模型。

主成分分析;大坝变形;BP神经网络

大坝安全监测数据处理模型通常采用的数学模型主要有统计模型、确定模型、混合模型等(李珍照，1997)。其中统计模型和混合模型一般多采用回归分析方法来建立，对事先拟定的因子进行筛选及系数求解，但所选的因子之间有时会存在严重的相关性，这种相关性有时会对预测效果产生较大的影响。目前对拟定大坝变形影响因子进行系数求解的方法主要采用的是相关性判别法。这种方法虽然能准确确定每一个影响因子与大坝变形的相关性，但经过相关性判别只是线性地确定大坝位移影响因子与大坝变形量之间的关系，并没有对影响因子之间的相关性进行分析，并且由于影响因子之间存在相关性，将会引入大量无效变量。主成分分析可以有效地解决变量之间的多重相关性问题(农吉夫等，2008)。本文主要利用主成分分析构造神经网络学习矩阵，将主成分分析与BP神经网络相结合，同时将传统的BP网络进行了改进，引入了动量训练算法，降低了网络对于误差曲面局部细节的敏感性，有效地抑制了网络陷入局部极小的问题。建立大坝变形预测模型，通过matlab编程实现，并将预测结果与BP网络模型、灰色模型进行对比分析，得出基于主成分分析的BP神经网络可以有效地降低输入因子的维数，减小因子之间相关性的影响，简化网络结构，降低网络训练难度，提高了预测的稳定性及精度。

1 基于主成分分析的大坝位移影响因子的判断

主成分分析(吴翊等，1995)是研究多个变量间相关性的一种多元统计方法。通过少数几个主分量解释多变量的方差，即导出少数几个主分量，使他们尽可能完整地保留原始变量的信息，且彼此不相关，以达到简化数据的目的。

现以广州蓄能水电厂河床坝段坝顶的2#观测点2000年4月12日至2003年4月16日Y向水平位移观测值为例，说明主成分对大坝位移影响因子的判定的重要性，考虑到大坝位移产生的原因主要由扬压力、温度、时效引起，因此，将h，h2，h3，h4，h5，θ，θ2，θ3，θ4，θ5，lnθ，sinG，cosG，sinG*cosG，sin2G，T0(h为上游水位值，θ为观测值当天到起测日之间的累计天数除以100，G=2πt/365，t为观测时刻距初始时间的天数)作为大坝位移的影响因子，如果直接将这16个影响因子作为神经网络的输入因子，必然会引入一些冗余的影响因子，所以必须对影响因子与大坝位移的相关性进行判定，本文采用pearson相关性判别法。假定大坝位移量为y，大坝位移影响因子中的各个影响要素用x表示，根据普济(2008)pearson相关系数

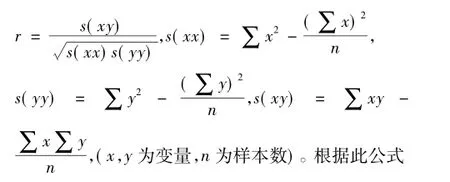
表1 影响因子与大坝位移之间的pearson相关系数Tab.1 The pearson coefficient between impact factors and dam displacement

根据Pearson相关性显著性表，确定T0，sinG，cosG，h，h2，h3，h4，h5与大坝位移量显著相关。同时，扬压力影响因子h，h2，h3，h4，h5相互之间完全相关。如果将扬压力影响因子h，h2，h3，h4，h5全部作为神经网络的输入因子，势必会造成信息的重叠。同时自变量之间的相关性较大，使输入矩阵为病态，神经网络求得的解不稳定，且收敛速度很慢(李雪红等，2001)。主成分分析法就是将彼此之间相关性比较大的影响因子进行简化，同时又不影响原有影响因子所代表的信息。对扬压力影响因子的51个样本进行主成分分析，每个样本共有5个指标(变量)对其进行描述。这样便构成了阶的数据矩阵H:变量H有不同的量纲，由此会引起各变量取值的分散程度差异较大，这时变量H的总方差受方差较大的变量控制，若由原变量的协方差矩阵出发进行主成分分析，则优先考虑了方差较大的变量，不仅给主成分变量的解释带来困难，还会造成不合理的结果。所以为了消除原变量彼此方差差异过大的影响，则需将原变量进行标准化处理。标准化之后得到矩阵H1:

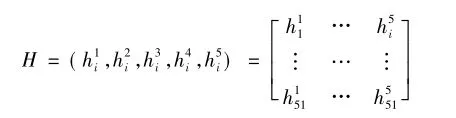
H1与原始变量H的结构完全相同，代表了原始变量所有信息。对标准化后的变量H1做线性组合分析，得出新的变量指标Hk:

变量Hk的维数相对于H得到了降低，同时它又能包含变量H中的大部分信息。最终将Hk，T0，sinG，cosG作为大坝位移的影响因子。

2 基于BP网络的实例分析

2.1 BP网络模型构建

BP神经网络即误差后向传播神经网络是目前神经网络中使用最广泛的一类。从结构上，BP网络是典型的多层网络，分为输入层、隐含层和输出层，层与层之间多采用全互联方式，同一层单元之间不存在相互连接(黄红女等，2003)。神经元结构同普通神经元结构类似(危志明等，2009)，只是为了学习算法的推导，将阀值的作用等效为第0个输入端，该输入端的输入值恒定为1，并且令w0=－θi，于是神经元的输出为:

输入层接收信息经隐含层作用函数处理后传出到输出层。

2.2 BP算法改进(参数的选取)

BP网络构建过程中训练函数的选取及训练过程中学习速率的选取将直接影响到训练时间、稳定性及预报精度。本文基于BP算法(刘金生等，2008)的主要缺点:收敛速度慢、局部极值、难以确定隐含层和隐含层节点个数。从而提出了启发式的学习算法，就是对于表现函数梯度加以分析，从而改进算法，传统的BP网络训练过程是沿着负梯度方向调整权值，并没有考虑到以前积累的经验，即以前时刻的梯度方向，从而常常使学习过程发生振荡，收敛缓慢。而动量梯度下降法将动量因子加入到权值调整过程中，可得:

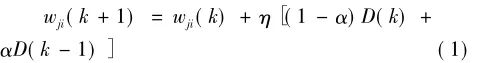
其中，D(k)表示k时刻的负梯度，D(k－1)表示k－1时刻的负梯度，η为学习率，α∈［0，1］是动量因子。所加入的此动量项减小了学习过程的振荡趋势，改善了收敛性。但实践表明，BP网络学习过程中学习速率η，动量系数α等值的选取，将直接影响到训练时间和成果精度(赵斌等，1999)。目前对BP网络中学习速率，动量系数的确定没有统一的计算模式，只能通过不断训练，根据经验做出判断，笔者多次对不同的η，α进行训练、预测。确定学习率α=0.05，动量因子α=0.7作为网络的训练参数比较合适，此时网络训练较为稳定，网络预报精度较高。

3 实例分析

3.1 隐含层节点数确定

将经过主成分分析所确定的大坝位移影响因子作为BP网络的输入量，以广州蓄能水电厂河床坝段坝顶的2#观测点2000年4月12日至2003年4月16日Y向水平位移观测值作为输出因子，在BP网络训练，预报之前，需要确定网络隐含层节点数。目前对BP网络隐含层节点数的确定主要采用0.618黄金分割法，经验公式法。由于黄金分割法计算较为繁琐，并且BP神经网络的训练存在偶然性，一次性黄金分割法所确定的隐含层节点数不一定是最佳的。本文将给予经验公式o=2m+1(o为隐含层节点数，m为输入节点数)外加多次训练逐步试探确定最佳隐含层节点数。经验公式所确定的隐含层节点数如表2所示。

表2 基于经验公式的隐含层节点数Tab.2 The hidden layer nodes based on empirical formula

基于BP网络，在经验公式所确定隐含层节点数两边进行不断训练，不断试探，为了体现公平训练，公平预报原则，训练参数都将统一设置，为了避免训练和预报的偶然性，对于每一个节点数都采取训练8次，预报8次，训练和预报结果的平均误差如表3所示。

表3 最佳隐含层节点数Tab.3 The best hidden layer nodes

从表3可以看出对于由主成分分析法所确定的影响因子BP网络预报模型，其最佳隐含层节点数为9，传统方法所确定的影响因子BP网络预报模型，其最佳隐含层节点数为17。

3.2 对比分析

将建立好的BP网络输入样本数据进行预报。由于原始观测数据的单位不同，因此需要对原始数据的自变量和因变量进行归一化处理，本例中的BP神经网络方法的激活函数采用sigmoid函数，故将输入数据归化到(－1，1)可提高网络的收敛速度;函数的因变量范围为(－1，1)，故网络的输出值也应归化到(－1，1)归一化公式如下:

式中xmax，xmin分别为每组因子变量的最大值和最小值;x，x'分别为每组因子变量规格化前和规格化后的值。

选取归一化后的前40组数据作为BP网络的训练样本，对于后11组数据进行预测，并用来与原始观测数据建模的BP神经网络模型、灰色模型预测结果进行对比分析，为了避免训练和预报的偶然性，采取对不同方法所确定的影响因子分别训练8次、预报8次的原则，对8次预测结果平均值进行对比分析(图1，表4)，预测残差如图2所示。

表4预测结果Tab.4 The prediction results mm

从图1和图2中可以明显看出，基于主成分分析的BP网络预测精度及稳定性明显优于BP网络模型、灰色预测模型。

4 结论

(1)由本文模型和算例可以看出将主成分分析法与BP神经网络相结合，可以有效地降低输入因子的维数，减小因子之间相关性的影响，简化网络结构，降低网络训练难度，提高了预测的稳定性及精度。同时将传统的BP网络进行了改进，引入了动量训练算法，降低了网络对于误差曲面局部细节的敏感性，有效地抑制了网络陷入局部极小的问题，其收敛性比传统的BP网络要好，由此得出结论，基于主成分分析与BP网络相结合的预报模型精度及稳定性明显优于其他模型。

(2)在大坝变形预测之前，需要引入大量的前期观测数据，而观测数据中的无效数据将直接影响到大坝预测的稳定性及精度，怎样剔除观测数据中的无效数据将有待进一步探讨。

李珍照.1997.大坝安全监测［M］.北京:中国电力出版社.

农吉夫，金龙.2008.基于MATLAB的主成分RBF神经网络降水预报模型［J］.热带气象学报，24(6):713-717.

吴翊，李永乐，胡庆军.1995.应用数理统计［M］.长沙:国防科技大学出版社.

普济.2008.数理统计与应用第7讲 相关与回归(2)——相关系数［J］.中国质量，8:85-89.

李雪红，徐洪钟，顾冲时，等.2001.主成分神经网络模型在大坝观测资料分析中的应用［J］.大坝观测与土工测试，25(5):14-16.

黄红女，华锡生，王铁生.2003.利用反向传播神经网络实现大坝的综合评判［J］.水电自动化与大坝监测，27(2):56-58.

赵斌，吴中如，张爱玲.1999.BP模型在大坝安全监测预报中的应用［J］.大坝观测与水土测试，23(6):1-3.

刘金生，周焕银，刘金辉.2008.基于BP神经网络的抚河水环境质量评价研究［J］.东华理工大学学报:自然科学版，31(1):85-88.

危志明，吴良才.2009.基于GADS工具箱的GPS高程拟合方法［J］.东华理工大学学报:自然科学版，32(1):89-92.

The Dam Deformation Forecasting of BP Neural Network and Principal Component Analysis

ZHANG Jian-xi， ZANG De-yan
(Faculty of Surveying Engineering，East China Institute of Technology，Fuzhou，JX 344000，China)

The principal component analysis with the BP neural network is applied to the optimization of dam deformation impact factors，build the dam deformation forecast model.It can effectively reduce the input factor of dimensionality，simplify network structure，reduce network training difficulties，improve the stability and precision，reduce the correlation between the impact of factor and the efficiency of BP network training is improved，a large number of factors are introduced by the correlation between factors are resolved.The result shows that the accuracy and stability are predicted by the application of BP neural network based on principal component analysis is better than other models.

the principal component analysis;dam deformation;BP neural network

TV698.2+3

A

1674-3504(2011)03-288-05

10.3969/j.issn.1674-3504.2011.03.014

2010-12-31

江西省教育厅重点科技项目(GJJ10022)

张建喜(1986—)，男，硕士研究生，主要从事海洋地形测绘理论与应用方向。