一类2个自由度Hamilton系统的动力学性质*
2011-12-17林路婵赵晓华
林路婵, 赵晓华
(浙江师范大学数理与信息工程学院,浙江金华 321004)
0 引言
考虑一类关于电场中沿着z轴传播的、缓慢变化的复包络或分量φm(z,t)的N耦合非线性类Schrödinger方程

式(1)中:φ*m是φm的共轭函数;p,q,κ是媒介的特征参量;下标m表示φ的不同分量;下标z,t表示对φ 关于 z,t求导.
将驻波解φm(z,t)=xm(t)exp(iΩ z)代入方程(1),可得如下的耦合非线性方程:

对于系统(2),文献[1]通过待定系数法得到了在参数bmn=±1,∀m,n=1,2,…,N的情况下的Legendre函数形式的解
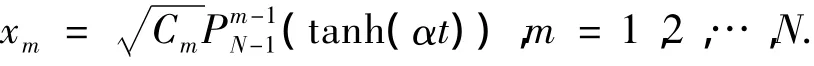
笔者将考虑N=2的情形,系统(2)即为
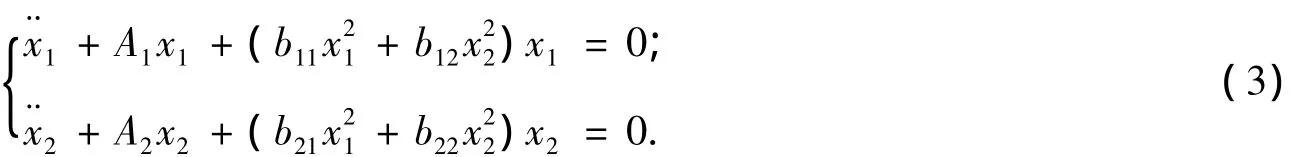
系统(3)在许多实际物理问题中有着广泛的运用.文献[2-4]中所涉及的非线性偏微分方程,通过求其特殊形式的解均可转化为本文所要研究的二阶常微分方程组.
对于系统(3),文献[5-6]在一些特定参数条件下分别给出了另一个与Hamilton量H是函数独立且对合的首次积分,从而说明系统(3)是完全可积的;文献[2]给出了可积情况下,对于一些特定的参数条Schrödinger方程的同宿轨问题.
对于参数b12,b21都不为零的情况,若b12,b21同号,则经过适当的尺度变换之后,可以得出系统(3)是具有2个自由度的Hamilton系统;若b12,b21异号,则经过相应的变换后,系统(3)是一个四维反转对称系统.
本文主要考虑在b12,b21均大于零的情形下,利用Hamilton系统的相关知识对系统(3)进行定性研究.
1 平衡点的个数及其类型分析
由于系统(3)含有6个非零参量,为了便于研究,将通过尺度变换以减少参量个数.
先令 A1=sgn(A1)ω21,A2=sgn(A2)ω22,其中 sgn(x)是符号函数.假设 b11>0,b22>0,作尺度变换
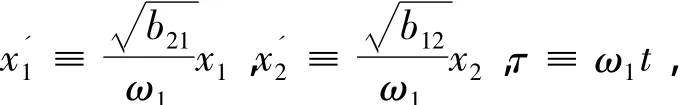
从而系统(3)变为

令˙x1=y1,˙x2=y2,则系统(4)可以改写为
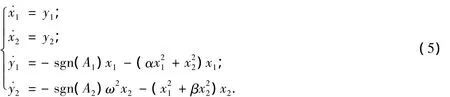
易知系统(5)对应线性系统的Jacobi矩阵为
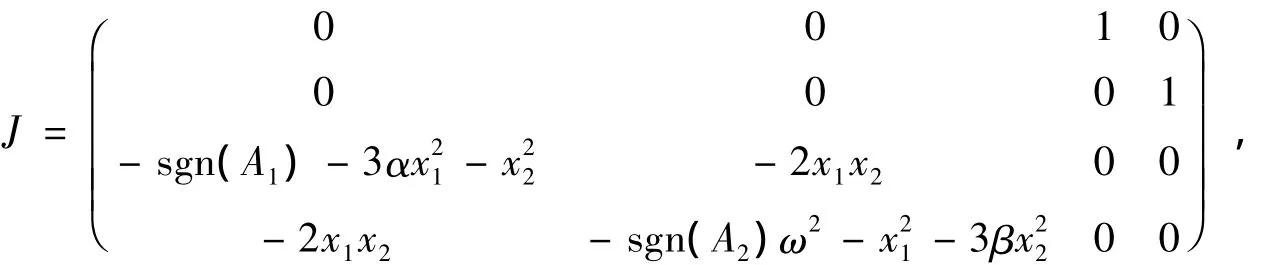
其对应的特征方程为
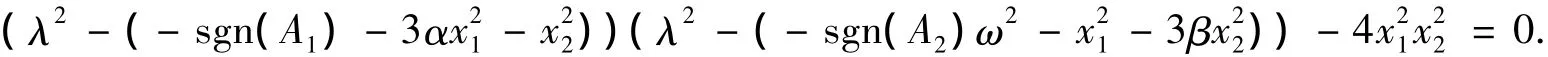
因此,求系统(5)的平衡点即为求方程组
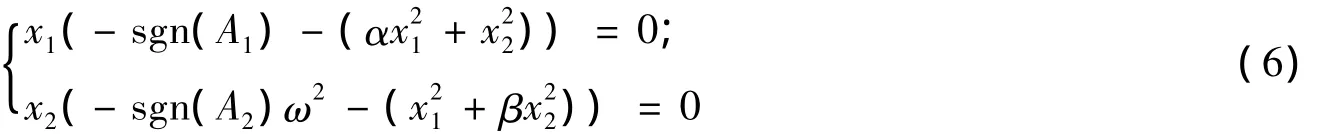
的零点.对系统(5)分以下几种类型进行讨论:
1)原点(0,0,0,0)是系统(5)的平衡点,所对应的特征方程为
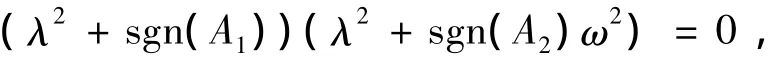
从而
①当A1>0,A2>0时,所对应的特征值为±i,±ωi,平衡点的类型为中心;
②当A1<0,A2>0时,所对应的特征值为±1,±ωi,平衡点的类型为鞍-中心;
③当A1>0,A2<0时,所对应的特征值为±i,±ω,平衡点的类型为鞍-中心;
④当A1<0,A2<0时,所对应的特征值为±1,±ω,平衡点的类型为鞍点.

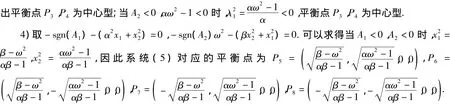
这里先假设根号下的式子为正,由于β-ω2=0或者αω2-1=0的情形可以归结到第2),3)种情形,所以只考虑 β - ω2,αβ -1,αω2-1 三者同号.根据矩阵 J在 Pj(x1,x2,0,0)(j=5,6,7,8)处的特征方程
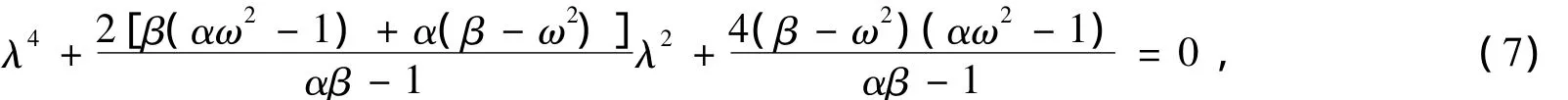
并记
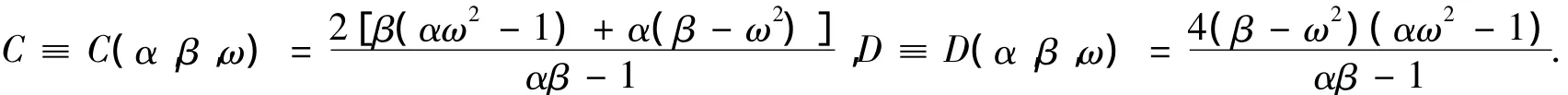
因此 C >0,且
①当αβ-1<0,即D<0时,方程(7)有特征值
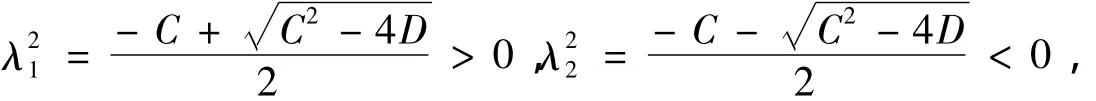
因此平衡点 Pj(x1,x2,0,0)(j=5,6,7,8)的类型为鞍-中心型.②当 αβ-1>0,即 D >0时,由于

所以方程(7)有特征值
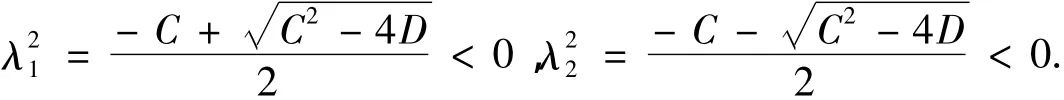
因此平衡点 Pj(x1,x2,0,0)(j=5,6,7,8)的类型为中心型.
综上,可以得到关于系统(5)平衡点的个数及其类型的定理.
定理1 系统(5)的平衡点个数及其类型为:
1)当A1>0,A2>0时,有唯一的平衡点(原点),其类型为中心.
2)当 A1>0,A2<0 时,原点为鞍-中心,平衡点 P1,P2均为中心.
3)当 A1<0,A2>0 时,原点为鞍-中心,平衡点 P3,P4均为中心.
4)当 A1<0,A2<0 时,原点为鞍点,且
①当β-ω2>0时,平衡点Pj(j=1,2)为鞍-中心;
②当β-ω2≤0时,平衡点Pj(j=1,2)为中心;
③当 αω2-1>0时,平衡点 Pj(j=3,4)为鞍-中心;
④当αω2-1≤0时,平衡点Pj(j=3,4)为中心;
⑤当 β -ω2>0,αω2-1 >0 时,平衡点 Pj(j=1,2,3,4)均为鞍-中心;
⑥当 β -ω2>0,αω2-1≤0 时,平衡点 Pj(j=1,2)为鞍-中心,平衡点 Pj(j=3,4)为中心;
⑦当 β -ω2≤0,αω2-1 >0 时,平衡点 Pj(j=1,2)为中心,平衡点 Pj(j=3,4)为鞍-中心;
⑧当 β -ω2≤0,αω2-1≤0 时,平衡点 Pj(j=1,2,3,4)均为中心;
⑨当 β-ω2>0,αω2-1 >0,αβ -1 >0 时,平衡点 Pj(j=1,2,3,4)均为鞍-中心,Pj(j=5,6,7,8)均为中心;
⑩当 β-ω2<0,αω2-1 <0,αβ-1 <0 时,平衡点 Pj(j=1,2,3,4)均为中心,Pj(j=5,6,7,8)均为鞍-中心.
2 动力学性质研究
由于平衡点个数众多,因此将主要针对原点的不同类型来分析系统(5)的动力学行为,对于其他的平衡点可以进行类似的研究.
1)A1>0,A2>0.根据定理1可知,原点O是系统(5)唯一的平衡点,且其对应的特征值为±i,±ωi.因此,根据Hamilton系统的Lyapunov中心定理可知,当ω≠整数,即±i与±ωi非共振时,在原点O的小邻域内存在2个二维不变流形,在每个不变流形中都含有一族单参数的周期轨,且当轨道的初始条件趋
2)A1<0,A2>0.此时系统(5)即为
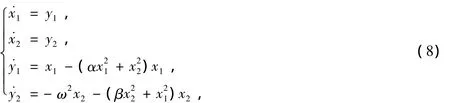
且其对应的Hamilton量为
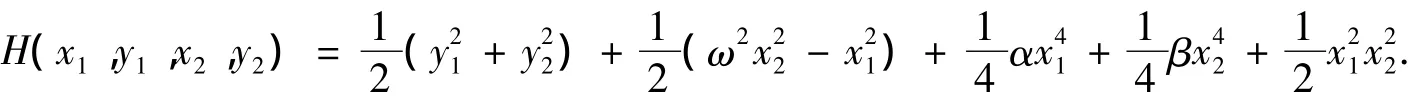
笔者将运用文献[8]的方法对原点附近的动力学行为进行分析.
若令 x=(x1,y1),y=(x2,y2),那么系统(8)可以简写成
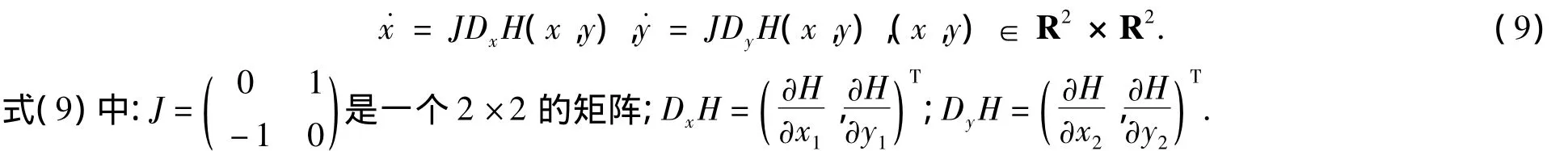
易知系统(9)具有如下性质:
①DxH(0,0)=DyH(x,0)=0,意味着x-平面({(x,y)|y=0})是它的不变平面.将˙x=JDxH(x,y)限制到x-平面上,可得˙x=JDxH(x,0),不动点x=0是它的双曲鞍点,且对应的同宿轨为
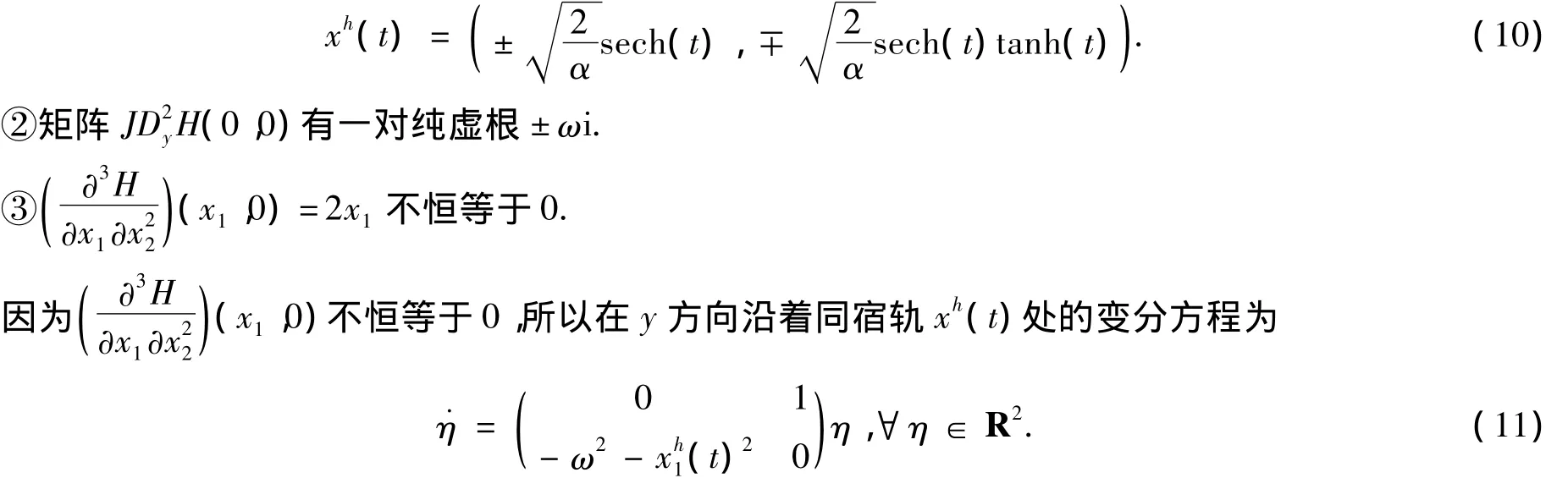
方程(11)可以改写为
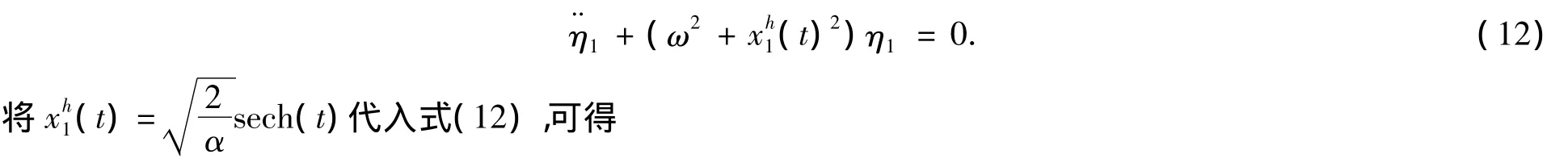
它所对应的解为
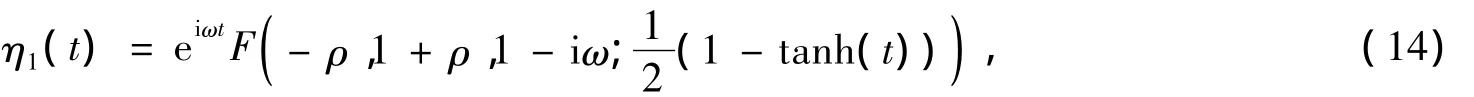
使得

计算式(14)可得

在其能量面上存在Smale马蹄.
4)A1<0,A2<0.此时系统(5)即为
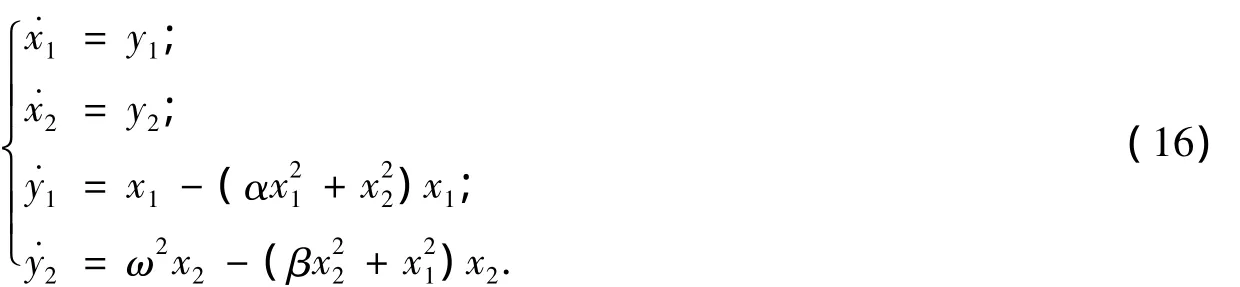
此处令 α =α0+εα1,β =β0+εβ1,ω2=ω0+εω1,并取 α0=β0=ω0=1,则系统(16)变为

当ε=0时,系统(17)是具有2个自由度的可积的Hamilton系统,它存在2个函数独立的首次积分
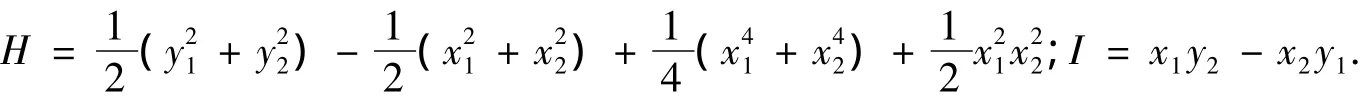
根据文献[2]可知系统(17)的无扰动系统存在一族同宿轨
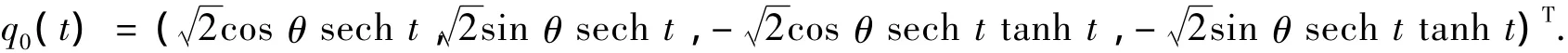
其中,θ是任意参量.
接下来将考虑在ε≠0时,运用Melnikov方法讨论系统(17)是否仍然存在同宿轨.此时可以将系统(17)写成
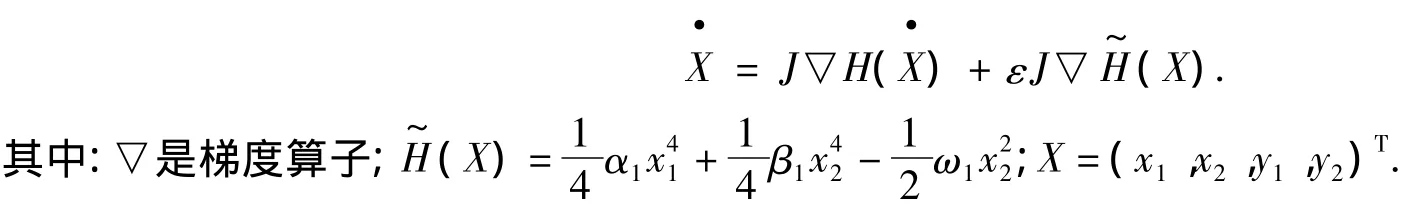
根据文献[9]计算其Melnikov函数,可得

并且

3 结语
主要考虑了b12,b21均大于零的情况下2个自由度的Hamilton系统在原点的附近邻域内所具有的周期轨、同宿轨以及混沌现象.对于b12,b21均小于零和b12,b21异号的情况,系统的动力学行为需进一步分析研究.
[1]Hioe F T.Solitary waves and N coupled nonlinear equations[J].J Phys:A Math Gen,1999,32(7):1217-1223.
[2]Yang Jianke.Classification of the solitary waves in coupled nonlinear Schrödinger equations[J].Physica:D,1997,108(1/2):92-112.
[3]Alagesan T,Chung Y,Nakkeeran K.Soliton solutions of coupled nonlinear Klein-Gordon equations[J].Chaos Solitons and Fractals,2004,21(4):879-882.
[4]Li Y.Singularly perturbed vector and scalar nonlinear schrödinger equations with persistent homoclinic orbits[J].Stud Appl Math,2002,109(1):19-38.
[5]Hioe F T.Hamiltonian systems with a certain stability property[J].J Phys:A Math Gen,1988,21(7):L377-L380.
[6]Baumann G,Glockle W G,Nonnenmacher T F.Singular point analysis and integrals of motion for coupled nonlinear Schrödinger equations[J].Proc R Soc Lond:A,1991,434(1891):263-278.
[7]张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,2006:101-119.
[8]Kazuyuki Yagasaki.Horseshoes in Two-Degree-of-Freedom Hamiltonian Systems with Saddle-Centers[J].Arch Rational Mech Anal,2000,154(4):275-296.
[9]Wiggins S.Global Bifurcations and Chaos[M].New York:Springer-Verlag,1988:334-457.
