专家克里金插值法在空间插值中的应用

刘世翔，胡艳飞，闫清华，马金苹，金 鑫

（中海油研究总院，北京100027）

专家克里金插值法在空间插值中的应用

刘世翔，胡艳飞，闫清华，马金苹，金 鑫

（中海油研究总院，北京100027）

克里金插值是一种进行局部估值的方法，但它并不能对局部的地质特征进行智能分析.因此，在很多时候其插值结果不能体现数据的一种局部异构特征.针对这一问题，提出了一种专家克里金插值法，这种方法是在普通克里金插值法的基础上加入专家地质知识，使得插值结果更能符合实际的地质情况.对该方法的原理、模型进行了详细的论述，并通过实例验证该方法的有效性.

专家克里金插值；异构特征；局部估值；空间结构

0 引言

在分析地质数据的过程中，很多时候是通过已知数据来预测未知数据，而未知数据的预测实质上是一个统计的过程［1-2］.地质统计学的核心是克里金法［3］，克里金法不仅能对不规则格点进行插值，而且还能根据多种要素场信息对某一要素场进行协同插值，克里金法既是一种对非均匀取样的内插方法，同时也是空间分析手段，最重要的是具备误差估计能力［4-5］.然而克里金插值是一种进行局部估计的方法，本身也存在着局限性，它在插值的过程中不能考虑实际的地质情况.在地质数据中，数据的分布总是具有一定的趋势性和异构性，分布趋势反映了数据的空间展布范围和趋势特征，异构性是指空间数据的局部差异性，在一个区域中的空间数据虽然有相同的数值，但是代表着不同的含义［6-7］.因此，本文提出一种“专家克里金插值法”，该方法就是利用地质专家对该区域的认识，建立对数据进行插值的限制条件，将数据在限制条件的基础上进行插值，使得插值结果更能体现地质专家的思想和实际地质的情况，最终提高区域插值数据的精度.

1 专家克里金插值法的提出

克里金插值是一种进行局部估计的方法.它所提供的是区域化变量在一个局部区域的平均值的最佳估计量.但在一些情况下，在整个区域上也存在局部的形态，而且数据分布的形态需要符合实际的地质特征，满足数据分布的区域性.例如，在对储集层的砂岩厚度进行插值时，砂岩的分布应该与该区域的沉积相所对应.也就是说每个沉积相应对应着自己的砂体特征，不同沉积相中的砂体不能因为厚度相同就连结成一个等值线，它们虽然值相同但代表的意义却是不同的，因此对于这种情况要对它们进行限定，将它们限定在各自的区域内，以此将它们区分开来.这就需要根据地质专家对该区域的地质实际情况对插值方法作某种限定，使得插值后的等值线的形态符合实际的地质特征.为解决这一问题，本文提出一种“专家克里金法”，该方法的思想是通过对实际地质资料的研究，掌握该地区的实际地质情况，根据实际的地质特征提取出边界限制条件，在边界限制条件的基础上进行空间数据插值.本研究主要考虑的是盆地边界和沉积相分布边界.这些边界条件是地质专家通过实际的地质资料研究出来的结果，是地质专家知识的体现.专家克里金法就是要将这些专家知识注入到插值算法里，使得插值结果充分体现出地质专家的知识，这样计算出来的插值结果更能符合实际地质特征.

2 专家克里金插值法的基本原理

专家克里金插值法是在克里金插值法基础上加入专家地质知识，因此该方法也具备克里金插值法的特点［8-9］.该方法不仅考虑了已知点和待估点的影响，而且利用协方差函数来定量考虑已知点的影响.

设Y（x）为区域变量，且是2阶平稳的，Y（xi）（i=1，2，···，n）是区域上xi（i=1，2，···，n）上的值，要对x0点处进行估值，所用的估计量为：

上述公式是n个数值的线性组合，而克里金方法中，求取λi的条件是保证估计量是无偏的，且估计方差最小.

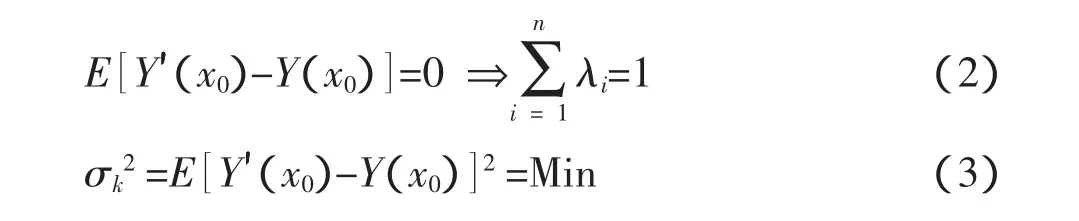
无偏差条件下，为了使估计方差最小，要应用拉格朗日乘数法求条件极值［10］，

（i=1，2，···，n）

最后得到克里金方程组，

（j=1，2，···，n）

3 专家克里金插值法的模型

专家克里金插值法的本质是要在专家知识的指导下对区域数据进行插值，使插值结果充分体现出地质专家在该区通过基础地质研究得到的地质认识，使得插值结果更能表现出实际的地质形态.在这一思想下，专家克里金插值法主要利用沉积相的分布特征以及盆地的边界条件，对插值数据进行专家知识的限定插值.综上所述，将按照图1所示的流程，建立专家克里金插值法模型.专家克里金插值法模型的建立主要包括以下几个内容：

图1 专家克里金插值法模型Fig.1 The model of expert kriging interpolation

（1）插值数据的生成.根据研究区内所要进行插值的参数，从数据库中提取出所有已知点的数据，生成带坐标的数据文件.

（2）通过对研究区的基础地质资料的研究，确定盆地边界和该层位的沉积相分布图，并将盆地边界和沉积相边界提取出来.边界的提取主要是提取边界上点的坐标，并使之首尾相连.提取的坐标越多对等直线的限定越精细，插值的结果越接近边界形状.

（3）克里金插值.在计算预测数据点时采用的还是克里金法，只是当等值线遇到边界条件的时候需要进行判断.若是盆地边界则等值线终止；若是沉积相边界等值线则不能越过等值线，而是要沿着边界的方向寻找边界内部的点进行连接生成等值线.

（4）绘制等值线.对预测数据点按照边界条件进行等值线的绘制.

4 应用

以某盆地砂岩测井解释数据为例，该区内沉积复杂，砂岩厚度变化快.该层位的沉积相主要有三角洲前缘、前三角洲、滨浅湖、深湖—半深湖和沙坝沉积（图2A）.本实例选用了该层位的200口井点的砂岩厚度数据进行插值方法对比，利用普通克里金插值法进行砂岩厚度插值（图2B）.插值后的结果与沉积相图进行对比分析，认为普通克里金插值法的砂岩厚度插值结果并没有反映出该层位的实际地质特征，普通克里金法不能很好地区分数据的异构特征.利用专家克里金插值法对该层位砂岩等厚图进行插值，结果如图2C所示.从插值结果可以看出，利用该方法计算的等值线与沉积相图的匹配效果更好，更符合实际地质特征，这个实例充分说明专家克里金插值法对数据插值的有效性.

图2 专家克里金插值对比Fig.2 Comparison between expert kriging interpolation and ordinary kriging interpolation

5 结论

专家克里金插值法，是在普通克里金插值法的基础上建立起来的，并且注入了专家的地质认识.因此它不仅具有普通克里金插值法的特征，而且还能充分体现了地质专家的思想和实际地质的情况，使得插值结果更能符合实际的地质特征.

利用专家克里金插值法，对研究区砂岩数据进行插值，插值结果不仅符合该区的地质特征，而且还提高了该区插值数据的精度，对该区以后的砂岩评价和油气成藏研究都有一定的指导意义.

［1］Cressie N A C.Statistics for spatial data［M］.NewYork:John Wiley and Sons,1991.

［2］Davis J C.Statistics and data analysis in geology（3rd edition）［M］.New York:John Wileyand Sons,2002:57—61.

［3］孙洪泉.地质统计学及其应用［M］.北京：中国矿业大学出版社，1990:38—39.

［4］弓小平，杨毅恒.普通Kriging法在空间插值中的运用［J］.西北大学学报：自然科学版，2008（12）:878—882.

［5］李晓军，王长虹，朱合华.Kriging插值方法在地层模型生成中的应用［J］.岩土力学，2009（1）:157—162.

［6］郭鹏，董兰芳，夏泽举.地质数据的等值线绘制方法研究［J］.计算机仿真，2009（9）:168—171.

［7］刘文岭，夏海英.同位协同克里金方法在储层横向预测中的应用［J］.勘探地球物理进展，2004（10）:367—370.

［8］阎辉，张学工.基于变异函数的径向基核函数参数估计［J］.自动化学报，2002（3）:120—126.

［9］刘湘南.GIS空间分析原理与方法［M］.北京：科学出版社，2003.

［10］程勖，杨毅恒.变异函数在异常空间插值中的应用［J］.世界地质，2007（3）:298—303.

APPLICATION OF EXPERT KRIGING ALGORITHM IN THE SPATIAL INTERPOLATION

LIU Shi-xiang,HU Yan-fei,YAN Qing-hua,MA Jin-ping,JIN Xin

（CNOOC Research Institute,Beijing 100027,China）

Kriging algorithm is a method for estimating geological features in a certain area.However,this kind of estimation is not an intelligent one.Thus,the result cannot show the heterogeneous characteristics of the estimated area.To solve the problem,the authors put forward the Expert Kriging Interpolation Method,which applies experts’geological knowledge in kriging interpolation,so that the result meets actual geological conditions.The theories and models of the Expert Kriging are described in detail.The effectiveness of such method is verified by case study.

expert kriging;interpolation;heterogeneous characteristics;local valuation;space configuration

1671-1947（2011）04-0292-03

P628

A

2011－02－25；

2011-03-30.编辑：张哲.

国家油气专项项目（XQ-2004-07）资助.

刘世翔（1978—），男，博士，工程师，主要从事数学地质与资源评价方面的研究，E-mail//lsxiang123@163.com