静电悬浮加速度计的地面重力倾角标定方法

薛大同

(中国空间技术研究院兰州物理研究所，兰州730000)

0 引言

静电悬浮加速度计是重力场测量卫星上的主要载荷之一，用于测量卫星受到的非重力，主要有:轨道高度处由于热层大气密度、水平中性风、太阳和地球的辐射压力引起的拖曳［1］，以及卫星自身产生的干扰力。为了准确恢复地球重力场，卫星在轨飞行时，需要以高的精度水平测定加速度计的标定参数，这需要靠在每天的几个弧段中处理GPS和加速度计数据，特别是使用可论证为最准确的重力场模型EIGEN－GL04C，和海洋潮汐模型 FES2004来实现［2］。然而，这绝不意味着加速度计飞行件在正式交付之前不需要作性能测试。为此，Marque等人指出，加速度计检验质量需要在地面重力下悬浮，以便为功能试验提供广泛的可能性。例如，加速度计传感头飞行件在环境试验前后需要开展悬浮状况、传递函数、标称静电刚度、线性、标度因数等综合试验，以检查完整的加速度计传感头状态和确认环境试验被通过，可以验收。这些试验是在专用的摆台上完成的，该摆台可以把悬吊平台精密控制在水平状态和实施倾斜摆动，并限制由地面重力投影引起的台面方向加速度在科学模式范围内［3］。法国ONERA早在上世纪90年代初就研制出双级摆台并用于静电悬浮加速度计噪声检测［4］，在世纪之交又采用主动控制技术抑制摆台低于0.1 Hz的干扰，这靠摆台上同时放置的另一台静电悬浮加速度计提供反馈控制信号来实现［5］。进入本世纪后推崇用摆台上成对静电悬浮加速度计噪声频谱差模来抵消共模环境噪声［6］，但存在原理上的错误［7］。Marque 等人近年来主要用摆台来做差分标度因数和二次因数验证［3］。本文在此基础上以SuperSTAR加速度计的性能参数为例，分析了在摆台上用传统的静态标定法确定模型方程各参数的困难，指出在摆台上无论是采用动态标定法大致判断标度因数和对成对加速度计进行模型方程各参数的一致性检验，还是采用电模拟法获取二阶非线性系数，都必须采取技术措施使得三阶非线性系数可以忽略。对动态标定法，提出了防止频谱泄漏和幅度谱中压低噪声干扰幅度的措施。对电模拟法，用实例给出了具体实施方案和效果。以上分析结果对GRADIO等更高指标的加速度计具有参考意义。

1 模型方程

根据等效原理，惯性加速度与引力加速度等效，因此地面上可以利用重力加速度在加速度计输入轴方向上的分量作为加速度测量标准，复现所需要的加速度值，实施地面重力倾角标定。此时静电悬浮加速度计的敏感轴如图1所示［8］，x轴处于负的铅垂方向。

理想情况下静电悬浮加速度计每个轴的反馈控制电压与该轴受到的加速度成正比［3］。以z轴为例，可表示为:

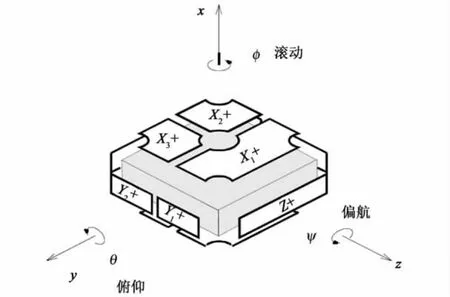
图1 静电悬浮加速度计的敏感轴［8］Fig.1 Sensitive axes of the electrostatically suspended accelerometer［8］

式中，Vz为z轴的反馈控制电压(V);Gp，z为静电悬浮加速度计反馈控制的物理增益(m·s－2/V)，并有［9］:

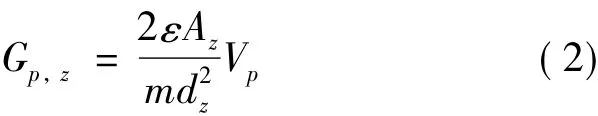
式中，ε为真空介电常数，ε =8.8542×10－12C2/(N·m2);Az为z轴的电极面积;m为检验质量块的质量;dz为检验质量块与z轴电极间的平均间隙;Vp为检验质量上施加的固定偏压。对于SuperSTAR加速度计而言，Az=2.08 ×10－4m2，m=7.2 ×10－2kg，dz=1.75 × 10－4m［10］，Vp=10V［11］，因此 Gp，z=1.67 ×10－5m·s－2/V。

实际上，静电悬浮加速度计与其他类型的加速度计类似，存在偏值、标度偏差、非线性、交叉耦合，因此，式(1)表达的γel，z并非z轴受到的实际加速度，而只是静电悬浮加速度计指示的加速度值(以下简称加速度计示值，单位m/s2)。

传统加速度计在地面重力下测试时的模型方程为［12］:

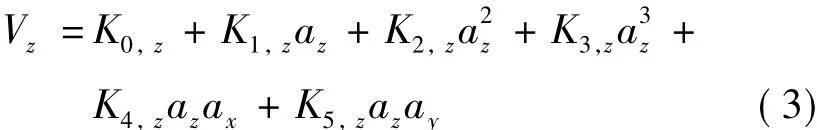
式中，K0，z为 z轴的偏值(V)，K1，z为 z轴的标度因数(V·m－1s2)，az为z轴的实际加速度 (m/s2)，K2，z为 z轴的二阶非线性系数 (V·m－2s4)，K3，z为z轴的三阶非线性系数(V·m－3s6)，K4，z为z轴和x轴的交叉耦合系数(V·m－2s4)，ax为x轴的实际加速度(m/s2)，K5，z为z轴和y轴的交叉耦合系数(V·m－2s4)，ay为y轴的实际加速度(m/s2)。

交叉耦合效应是加速度计某个敏感轴的偏值因该轴向及与之正交方向同时受到加速度作用而发生轻微改变的现象，变化量与这两个加速度的乘积成正比，比例系数称为交叉耦合系数。但是对于静电悬浮加速度计来说，情况有所不同。两个敏感轴之间的耦合主要来自于质量块的不平行度和不垂直度。为此，要求不平行度和不垂直度小于1×10－5rad(2″)，以保证在三个轴之间高解耦［13－14］。在此前提下，地面测试时铅垂方向残余耦合作用的恒定部分表现为偏值［15］，起伏不定部分表现为噪声［5］。另一水平方向的残余耦合作用可以忽略。因此，式(3)右端的最后两项不存在:

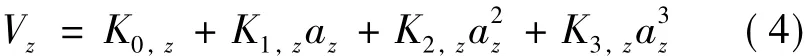
对照式(1)和式(4)，可知1/Gp，z为理论标度因数。SuperSTAR加速度计规定实际标度因数的偏差不超过2%［15］。即:

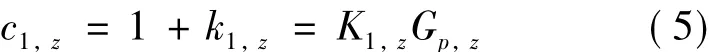
式中，c1，z为z轴实际标度因数与理论标度因数的比值，k1，z为 z轴的标度偏差，|k1，z| ＜ 0.02。

令:

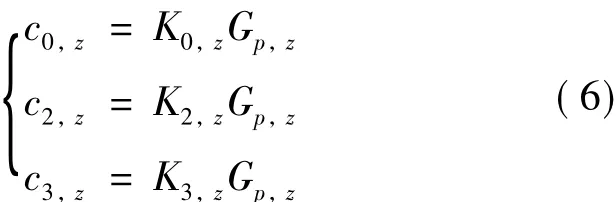
习惯上仍分别称 c0，z为 z轴的偏值 (m/s2)，c1，z为z轴的标度因数(无量纲)，c2，z为z轴的二阶非线性系数 (m－1s2)，c3，z为 z轴的三阶非线性系数(m－2s4)。

将式(1)、式(5)和式(6)代入式(4)，便可得到:

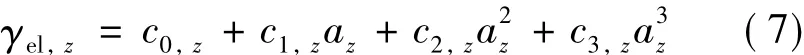
将式(7)简化表达为［15］:

需要注意的是，如前所述，地面重力下测试时得到的c0主要是铅垂方向残余耦合引起的，不同于在轨飞行时的偏值。

我们有:

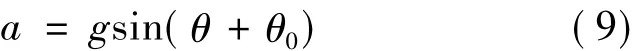
式中，g为当地的重力加速度值(m/s2)，θ为摆台的重力倾角(rad)，θ0为敏感轴与安装面间的夹角，即失准角(rad)。

实施地面重力倾角标定时，加速度计的输出必须处于量程范围内。以SuperSTAR加速度计为例，由于量程仅为 5μg［16］，所以 θ+ θ0不超过 5 ×10－6rad(1″)。在此极限条件下:

将式(10)代入式(8)，得到:

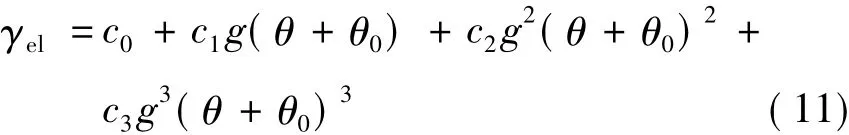
式(11)即为静电悬浮加速度计地面重力倾角标定的模型方程。

值得注意的是，加速度计敏感结构安装在经过研磨等精细加工的殷钢基座上，该基座的垂直度和平行度公差为5 ×10－5rad(相当于 10″)［4］，因此 θ0可以按不超过5×10－5rad估计。也就是说，为了使加速度计的输出处于量程范围内，θ必须部分抵偿θ0，以保证 θ+ θ0不超过5 ×10－6rad。

SuperSTAR加速度计射前检验的极限指标为:|c0|=1 ×10－5m/s2，c1=1.02，|c2|=10m－1s2，|c3|=3 × 105m－2s4［15］。

2 静态标定法

模型方程各参数传统采用静态标定法确定。对于静电悬浮加速度计来说，就应固定在专用摆台上，实施静态定标倾斜，先后调出若干个稳定不变、且精确知道其数值的θ，分别测出加速度计示值，并据此确定加速度计模型方程各参数。如第1节所述，θ0可以按不超过5×10－5rad估计;θ必须部分抵偿θ0，以保证 θ+ θ0不超过5 ×10－6rad。

由式(11)得知，未知数共有 5个:c0，c1，c2，c3，θ0，因此必须至少有5 个 θ值，对应5 个 γel值，形成5个方程。它们对于c0，c1，c2，c3来说，是线性方程，可以由其中4个方程用克莱姆法则联立求解，分别得到c0，c1，c2，c3对θ0的函数关系。原则上似乎将它们再代入第5个方程，就可以解出θ0，再分别代回 c0，c1，c2，c3对 θ0的函数关系，即可解出 c0，c1，c2，c3。但是对于θ0来说，是三次方程，有三个根，且运算极为复杂，从工程观点来说，精度也无法保证。所以迄今未见静电悬浮加速度计采用静态标定法的报导。

3 动态标定法

动态标定法的基本构想是:将静电悬浮加速度计固定在专用摆台上，摆台的倾角在加速度计通带范围内实施正弦摆动，对加速度计示值γel，z随时间变化曲线作频谱分析，根据幅度谱在各阶频率处的幅值确定加速度计模型方程各参数。

为了防止频谱泄漏，即防止在各次谐波峰的两旁出现旁瓣峰，影响主峰峰高，要保证整周期采样［7］。考虑到:① SuperSTAR的采样率为 10 Sps(Sampling per second)［15］，② 快速傅里叶变换的样本量必须为2的整数次幂［7］，③ 基频应在0.1 Hz附近［16］等三个因素，可选择摆动周期为6.4 s，即基频为0.15625 Hz，而且应足够稳定。

此时，摆台的重力倾角为［6］:

式中，θ1为摆台正弦摆动的最大角位移(rad)，不超过5μrad(1″);ω为摆动的角频率(rad/s);t为时间(s)。

将式(12)代入式(11)，并利用三角函数公式:

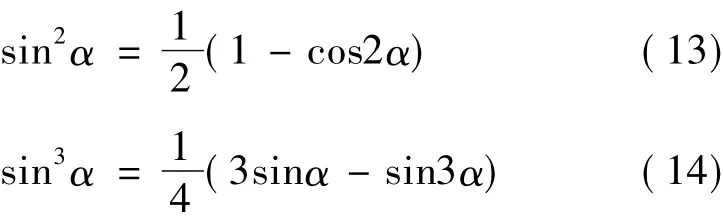
可以得到:

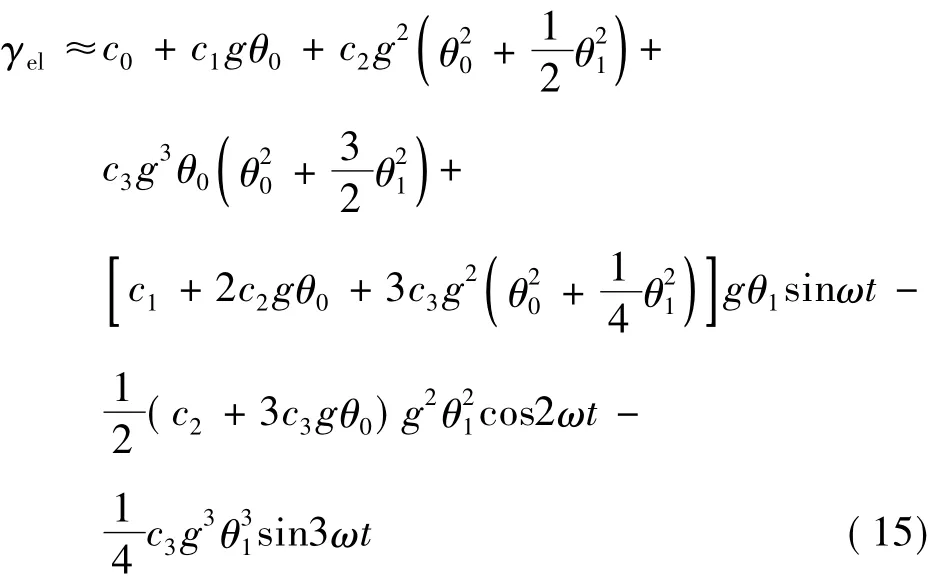
根据第1节所述极限值，我们取:c1=1，c2=是，从式(15)得到:

(3)在幅度谱的二倍频处，c2，c3θ0的贡献分别为1.2 ×10－8m/s2，5.3 ×10－7m/s2，也就是说，c2的贡献可能会被c3的影响所掩盖。

(4)在幅度谱的三倍频处，c3的贡献为8.8×10－9m/s2。

实际上，γel还受到环境振动噪声的干扰，包括地震噪声和人工振源产生的振动［14］。图2为法国ONERA实验室花冈岩台子上由静电悬浮加速度测到的噪声频谱，可以看到在基频至三倍频间(0.15Hz至0.47Hz)干扰大约在(3.5×10－7～1 ×10－6)m·s－2/Hz1/2之间［14］。由于实施正弦摆动时，摆台无法对噪声干扰实施主动控制;且摆台对此频段无被动隔振作用，所以摆台上的噪声干扰亦大致如此。如取采样率10 Sps，样本量213个［3］，依据频谱分析原理［7］，在幅度谱上基频至三倍频间噪声干扰的幅度将达到(1.73～4.94)×10－8m/s2。因此，二倍频处 c2的贡献、三倍频处c3的贡献将被噪声淹没。但如果样本量增加到218个，在幅度谱上基频至三倍频间噪声干扰的幅度将降低到(3.06 ～8.73) ×10－9m/s2，二倍频处 c2的贡献、三倍频处c3的贡献就可超出噪声本底，不被淹没。数据量越大越清晰。

从以上分析可以看到，由于专用摆台的振动噪声干扰，动态标定法很难精确测定c3。由于无法分离出θ0，受到θ0和c3的影响，加速度计模型方程的其他各参数均无法确定。

如果c3可以忽略，则情况要好得多。此时，零频处的幅值主要是c0和θ0的贡献，从基频处的幅值可以大致判断c1的大小，从二倍频处的幅值可以大致判断c2的大小。也就是说，主要问题只剩下无法分离 c0和 θ0。

4 检验二阶非线性系数的方法

二阶非线性系数起因于加速度计笼的最终缺陷，例如在相对电极表面或在电子元件真实数据中的差异。结果是，施加的静电力中心与笼中心不完全相配［3］。

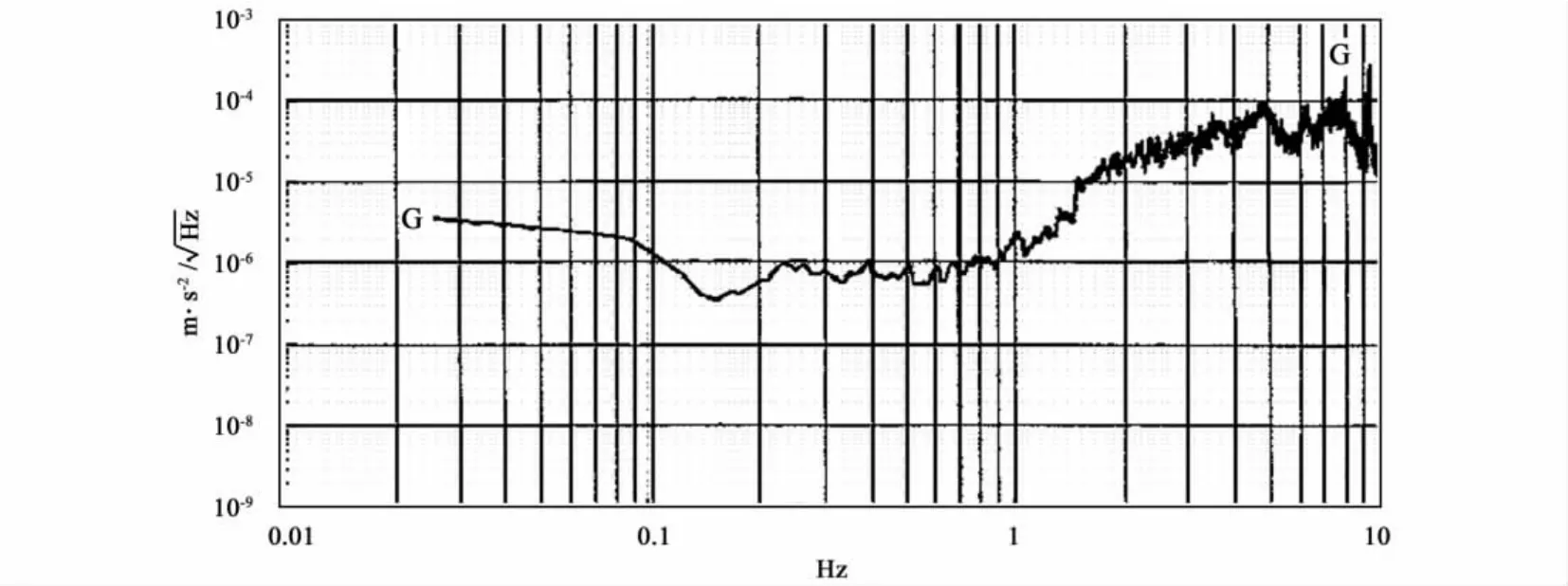
图2 在地面上测到的加速度频谱［14］Fig.2 Measured acceleration spectra on the ground［14］

第3节指出，采用动态标定法时，如果c3可以忽略，从二倍频处的幅值可以大致判断c2的大小。然而，在幅度谱上二倍频的幅度远低于基频的幅度，这种情况下摆台摆动的二次谐波不可以忽略［3］，此时，即使c3可以忽略，从二倍频处的幅值也无法判断c2的大小。理由如下:

当摆台摆动的二次谐波不可以忽略时，式(12)应改写为:

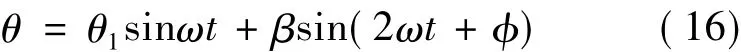
式中，β ≪ θ1，z。

忽略c3时，式(11)简化为:

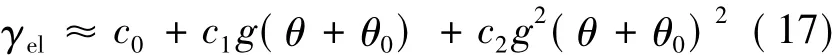
将式(16)代入式(17)，并利用式(13)及三角函数公式:

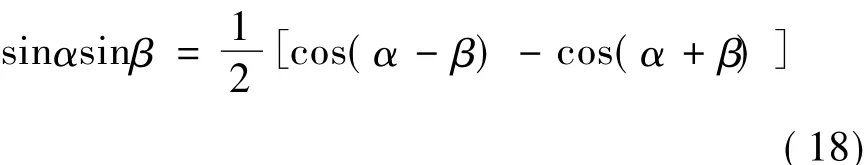
可以得到:

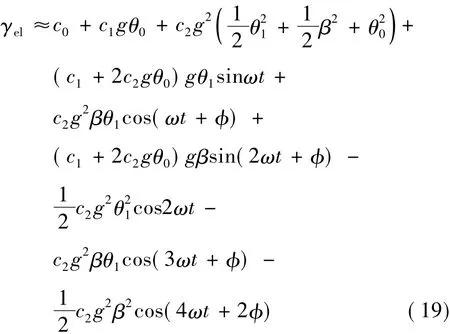
式(19)表明，加速度计示值幅度谱在二倍频处的幅度不仅与c2有关，还与摆台摆动的二次谐波幅度β有关。所以，摆台摆动的二次谐波不可以忽略时，不能用动态标定法得到c2。

为了检验c2，可采用电模拟的方法:摆台保持水平静止状态，在加速度计PID的输出处发送一个特定的二阶非线性系数标定信号［3］。这样做，既可以显著增加信号幅度，又可以保证信号不含二次谐波，还可以突出c2的贡献。

特定的二阶非线性系数标定信号为ASK(正弦载波数字幅度调制)信号，调制信号1，0等间隔排列。当c3可以忽略时，加速度计示值幅度谱在调制信号重复频率处的尖峰包含有c1和c2的作用。为了突出c2的作用，载波频率和幅度要尽量高，调制信号重复频率要尽量低。由于载波幅度高，加速度计噪声的影响可以忽略。

载波频率可超出加速度计回路带宽。载波幅度应保证带外抑制后的信号不超出加速度计测量范围。调制信号重复频率应处于加速度计测量带宽内。为了防止频谱泄漏，调制信号重复频率、采样率、载波频率间应符合2的整数次幂关系。

SuperSTAR加速度计闭环传递函数的幅频特性曲线如图 3 所示［10］。

以调制信号重复周期 25.6 s，即重复频率0.0390625Hz，载波频率320Hz为例，从图3可以看到，载波信号幅度将衰减至不足10%，考虑到SuperSTAR 加速度计测量范围 5 ×10－5m/s2［16］，载波幅度可以取 5×10－4m/s2，由第 1节所述 Super－STAR加速度计的物理增益可知相当于30 V，以此作为加速度的电模拟信号，若以ae表示，则加速度计感受到的加速度为a=ae+gθ0，以此代入式(8)，得到:

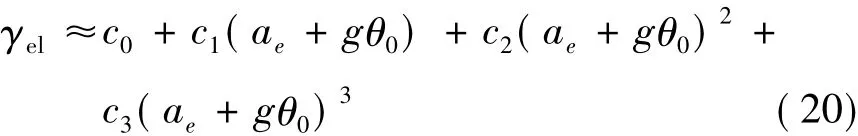
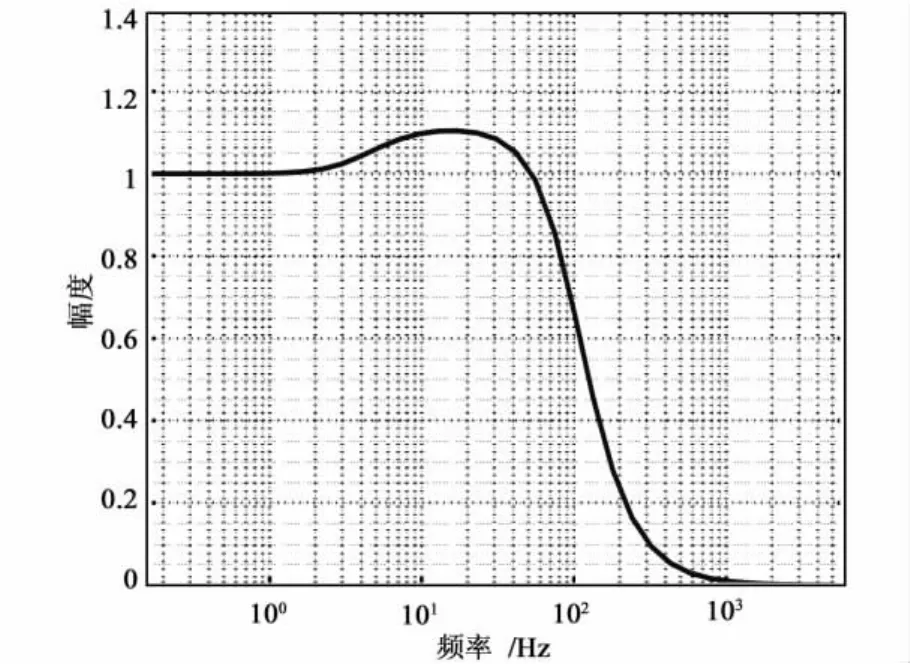
图3 SuperSTAR闭环幅频特性曲线［10］Fig.3 Closed loop magnitude－frequency characteristic curve of the SuperSTAR［10］

假设加速度计无通带限制，采样率5120 Sps，样本量220个，采用第3节的模型方程各参数，得到式(20)中的 c1(ae+gθ0) 项、c2(ae+gθ0)2项、c3(ae+gθ0)3项幅度谱分别如图4、图5、图6所示。可以看到，调制信号重复频率处的尖峰幅度在图4中最低，仅3.8 ×10－8m/s2;在图5 中其次，为8.0 ×10－7m/s2;在图6中最高，达到 3.5×10－5m/s2。也就是说，c2对调制信号重复频率处尖峰的贡献可能会被θ0和c3的影响所掩盖。而c1的影响不严重。所以，为了突出c2的贡献，必须设法使c3可以忽略。此时，式(20)变为:

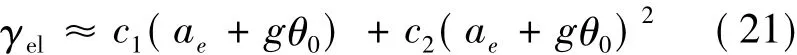
为了了解θ0对调制信号重复频率处尖峰幅度的影响，我们改设θ0=0 rad，而其他条件不变。此时，式(20)变为:

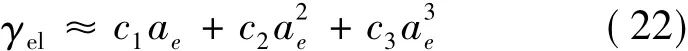
图7、图8、图9分别为式(22)中的c1ae项项项幅度谱。可以看到，调制信号重复频率处的尖峰幅度在图7中为3.8×10－8m/s2，与图4相同;在图8 中为8.0 ×10－7m/s2，与图5 相同;在图9中为1.9 ×10－9m/s2，仅为图 6 的 0.0054%。这说明θ0对调制信号重复频率处尖峰幅度的影响，仅限于c3的贡献。也就是说，当c3可以忽略时，不需要知道θ0的具体数值，就可以根据调制信号重复频率处的尖峰，确定c2的实际值。

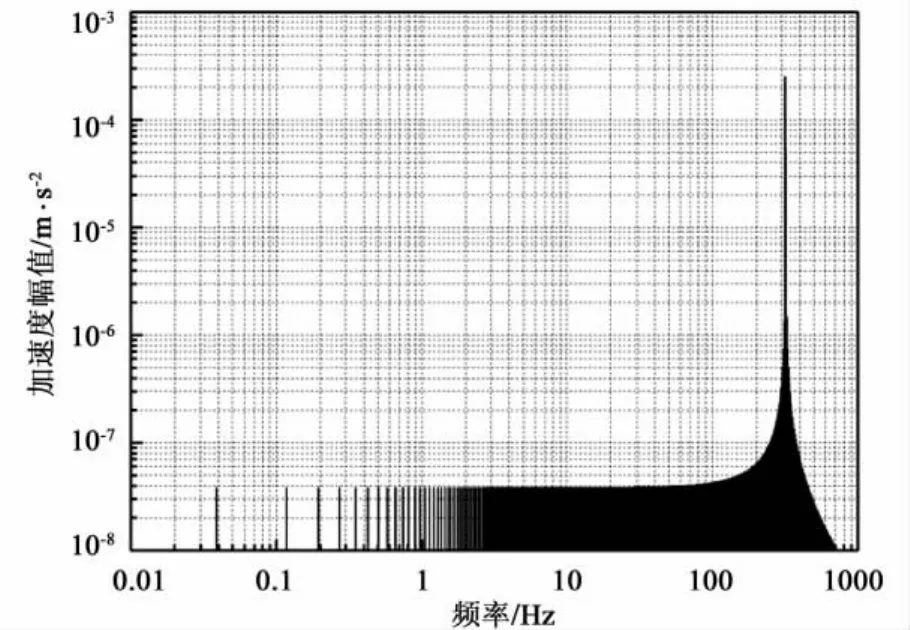
图4 在指定参数下的c1(ae+gθ0)项幅度谱Fig.4 Amplitude spectrum of the c1(ae+gθ0)item with the appointed parameters

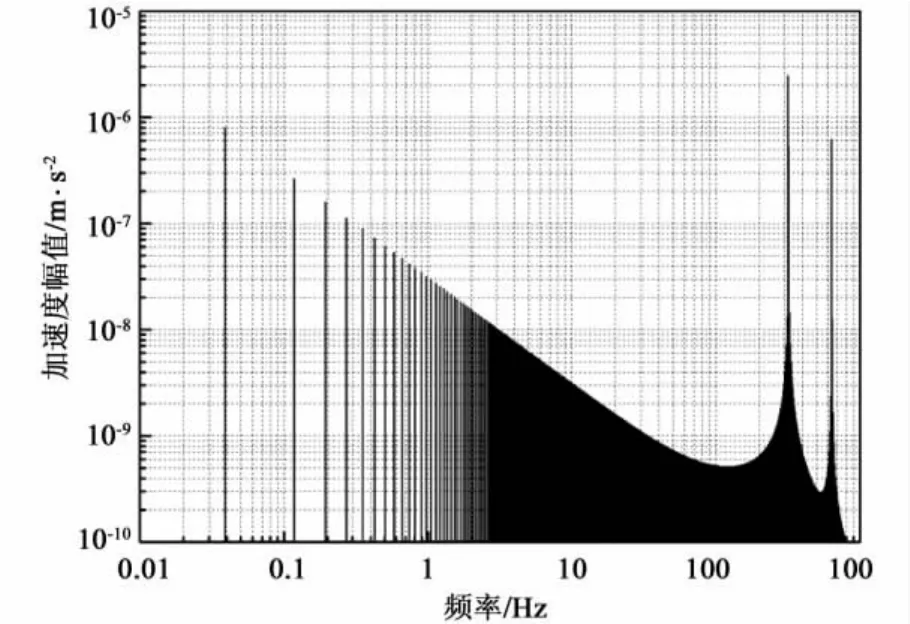
图5 在指定参数下的c2(ae+gθ0)2项幅度谱Fig.5 Amplitude spectrum of the c2(ae+gθ0)2 item with the appointed parameters

式(21)所示加速度计示值幅度谱如图10所示。可以看到，调制信号重复频率处的尖峰幅度为8.0 ×10－7m/s2，与图 5、图8 相同，证明它确实主要取决于二阶非线性系数。由于峰高与c2值成正比，由实际峰高便可确定c2的实际值。需要说明的是，实际检测加速度计示值时，由于受到测量通带的限制，得到的幅度谱在测量通带以外会受到抑制。至于实际采样率较低，样本量较少，只要有与之相应低通，从而符合采样定理，且样本量保证清晰识别调制信号重复频率，就不会影响判读。但如果实际采用的ASK信号与此不同，则应根据实际采用的ASK信号重新作频谱分析。

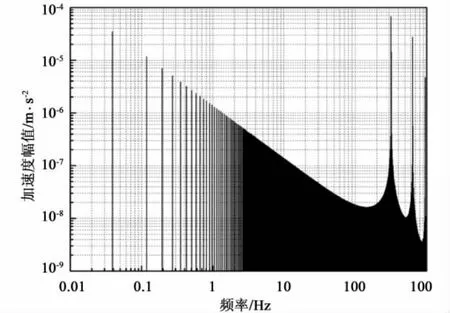
图6 在指定参数下的c3(ae+gθ0)3项幅度谱Fig.6 Amplitude spectrum of the c3(ae+gθ0)3 item with the appointed parameters

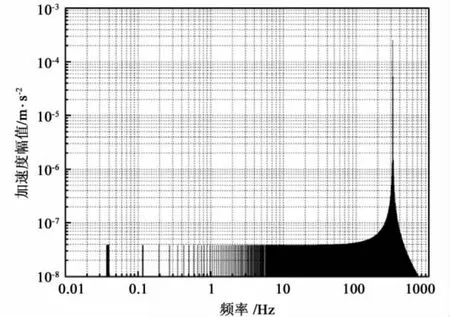
图7 在指定参数下的c1ae项幅度谱Fig.7 Amplitude spectrum of the c1ae item with the appointed parameters

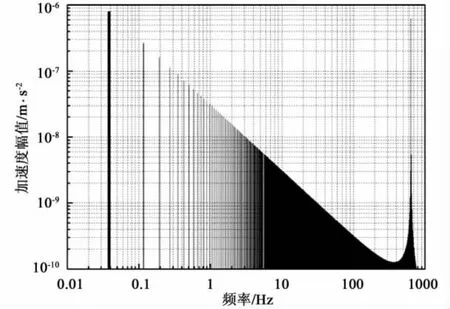
图8 在指定参数下的项幅度谱Fig.8 Amplitude spectrum of theitem with the appointed parameters

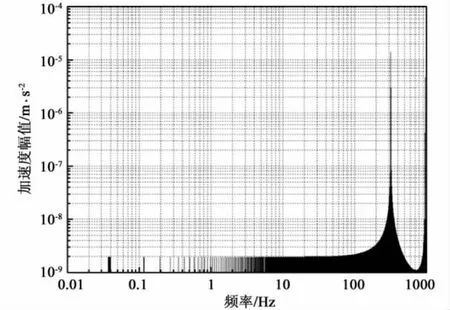
图9 在指定参数下的项幅度谱Fig.9 Amplitude spectrum of theitem with the appointed parameters

5 模型方程各参数的一致性检验方法

动态标定法可以用来直接检验两台加速度计模型方程各参数的一致性［3］。GRACE和GOCE均需要成对使用静电悬浮加速度计，特别关注每对加速度计的一致性，直接检验模型方程各参数的一致性是非常必要的。

成对加速度计同时固定在一个专用摆台上，摆台按照第3节的要求实施正弦摆动。将式(5)代入式(15)，得到两台加速度计示值幅度谱在基频处的幅度分别为:

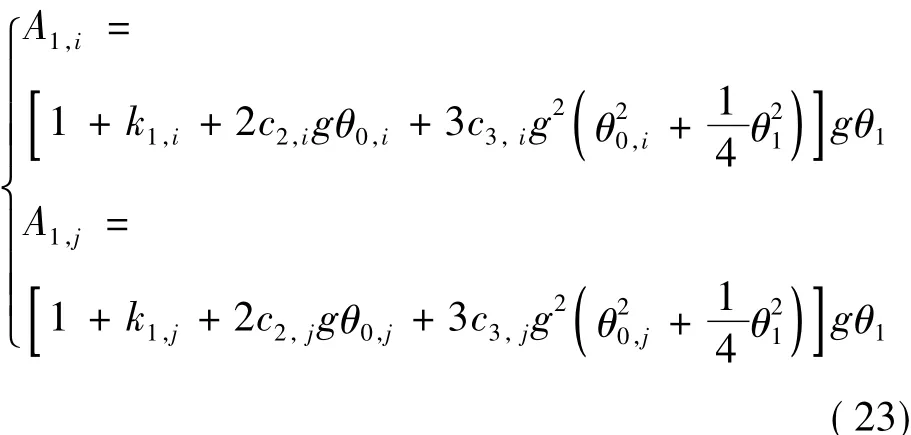
式中，对于编号 i和编号 j的加速度计，A1，i，A1，j分别为各自示值在基频处的幅度，k1，i，k1，j分别为各自的标度偏差，c2，i，c2，j分别为各自的二阶非线性系数，θ0，i，θ0，j分别为各自的失准角，c3，i，c3，j分别为各自的三阶非线性系数。

称两台加速度计示值的平均值为共模，半差分值为差模，则差模和共模幅度谱在基频处幅度之比为:

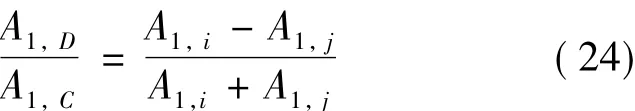
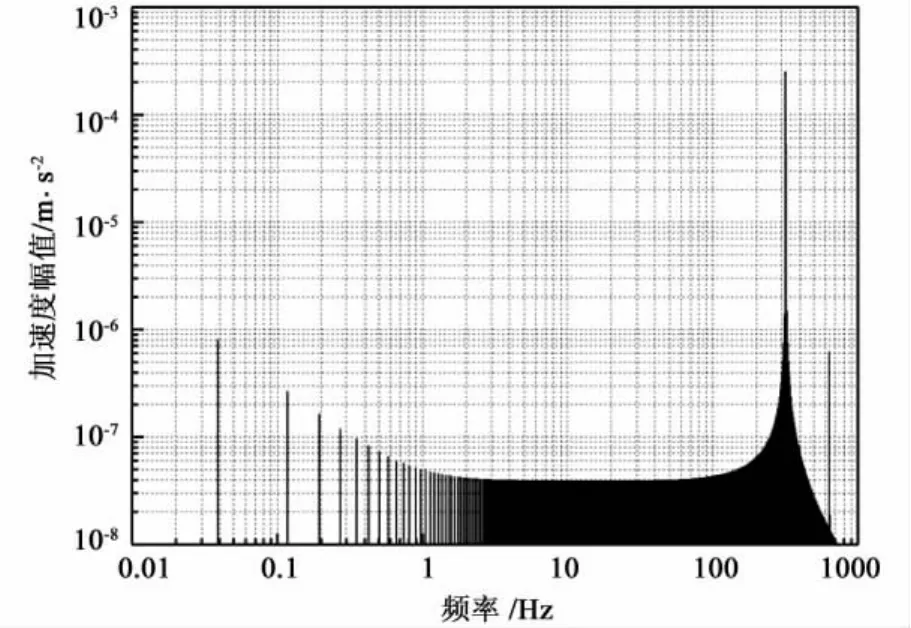
图10 在指定参数下的加速度计示值幅度谱Fig.10 Amplitude spectrum of the accelerometers indication with the appointed parameters

式中，A1，D为基频处的差模幅度，A1，C为基频处的共模幅度。将式(23)代入式(24)，并考虑到第1节所有参数的极限值，得到:

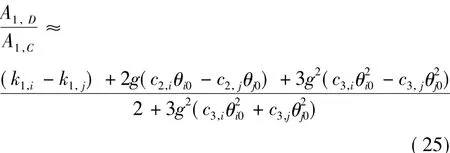
在第1节给出的参数极限值范围内，|k1|＜

(1)在第1节给出的参数极限值范围内，由式(25)得到的比值有可能主要反映两台加速度计c3，θ0的不一致性。只有当c3可以忽略时，c1的不一致性才占主要地位。

(2)式(25)得到的比值越小，两台加速度计的c3，θ0，进而 c1，c2越相近。

6 结论

(1)静电悬浮加速度计检验质量需要在地面重力下悬浮，以便为功能试验提供广泛的可能性。

(2)由于敏感轴之间的耦合机理不同于传统加速度计，所用的模型方程亦有所差别。

(3)地面重力下测试时，偏值主要是铅垂方向残余耦合引起的，不同于在轨飞行时的偏值。

(4)由于失准角远大于量程范围内的重力倾角，无法采用传统的静态标定法确定模型方程各参数。

(5)必须采取技术措施使得三阶非线性系数可以忽略，才能在专用摆台上用动态标定法大致判断标度因数和检验成对加速度计检验模型方程各参数的一致性，用电模拟法得到二阶非线性系数。

(6)动态标定作幅度谱分析时为防止频谱泄漏，即防止在各次谐波峰的两旁出现旁瓣峰，影响主峰峰高，要保证整周期采样。

(7)动态标定作幅度谱分析时可采用显著加大样本量的办法降低噪声干扰幅度。

(8)电模拟法只需摆台保持水平静止状态，并在加速度计PID的输出处发送一个特定的ASK信号，就可以根据调制信号重复频率处的尖峰，确定c2的实际值，而不需要知道失准角θ0的具体数值。

［1］ Flury J，Bettadpur S，Tapley B D.Precise accelerometry onboard the GRACE gravity field satellite mission［J］.Advances in Space Research，2008，42:1414－1423.

［2］ Bruinsma S，Biancale R，Perosanz F.Calibration parameters of the CHAMPand GRACE accelerometers［OL］.http://www.dgfi.badw.de/typo3_mt/fileadmin/20071015 － 17 － Potsdam/di_1800_05_bruinsma.pdf

［3］ Marque JP，Christophe B，Liorzou F，et al.The ultra sensitive accelerometers of the ESA GOCE mission［C］.The59th International Astronautical Congress，Glasgow，UK，September 28 －October 2，2008，IAC －08 －B1.3.7.

［4］ Bernard A，Touboul P.The GRADIO accelerometer:design and development status［C］.Proceedings of the Workshop on Solid －Earth Mission ARISTOTELES，Anacapri，Italy，1991，ESA SP－329，61－67.

［5］ Touboul P.μSCOPE［C］.ESA －CERN Workshop，Fundamental Physics in Space and Related Topics，CERN，April 5 －7，2000.

［6］ Touboul P.MICROSCOPE status［C］.GREX Workshop，Pisa，Italy，October 7－10，2002.

［7］ 薛大同.静电悬浮加速度计噪声测试数据的频谱分析方法［J］.空间科学学报，2008，28(1):55 －63.［Xue Da－tong.Method for spectral analysis of electrostatically suspended accelerometer noise data［J］.Chinese Journal of Space Science，2008，28(1):55 －63.］

［8］ Nati M，Bernard A，Foulon B，et al.ASTRE － a highly performant accelerometer for the low frequency range of the microgravity environment［C］.The 5th European Symposium on Space Environmental Control Systems and the 24th International Conference on Environmental Systems，Friedrichshafen，Germany，June 20－23，1994.

［9］ 薛大同.静电悬浮加速度计伺服控制分析［J］.空间科学学报，2009，29(1):102 － 106.［Xue Da－tong.Servo－control analysis of electrostatically suspended accelerometer［J］.Chinese Journal of Space Science，2009，29(1):102 －106.］

［10］ Frommknecht B. Simulation des sensorverhaltens bei der GRACE－mission ［D］. Diplomarbeit TUM (Technische Universität München)1874366，August 31，2001.

［11］ Davis E S，Dunn C E，Stanton R H，et al.The GRACE mission:Meeting the technical challenges［C］.The50th International Astronautical Congress，Amsterdam，Netherlands，October 4－8，1999，IAF －99 －B.2.05.

［12］ 何铁春，周世勤.惯性导航加速度计［M］.北京:国防工业出版社，1983:335.

［13］ Touboul P，Foulon B，Willemenot E.Electrostatic space accelerometers for present and future missions［C］.The 47th International Astronautical Congress，Beijing，China，October 7 － 11，1996，IAF －96 － J.1.02.

［14］ Touboul P，Foulon B.Space accelerometer developments and drop tower experiments［J］.Space Forum，1998，4:145-165.

［15］ Jet Propulsion Laboratory，University of texas center for space reserch，GeoForschungZentrum Potsdam.GRACE Science＆ Mission Requirements Document 327-200，Revision D［R］.March 6，2002，JPL D －15928.

［16］ Touboul P， Foulon B， LISA senseur gravitationnel ＆accéléromètres electrostatiques［C］，1ères journées LISA －France，Paris，Jan 20－21，2005.