飞行器复杂外结构的环境热流计算方法

孙 创，夏新林，戴贵龙

(哈尔滨工业大学能源科学与工程学院，哈尔滨150001)

0 引言

对于空间飞行器的热分析计算而言，真实可靠的环境热流模拟是获得精确温度场计算结果的前提保证。而环境热流的计算需要飞行器轨道动力学和热力学结合，是一个跨学科研究。目前，国外的外热流计算软件中，NEVADA是基于Monte-Carlo方法和电磁辐射理论模拟辐射换热过程的商业软件，STK为轨道分析软件，I－DEAS利用其轨道分析结果计算环境热流。以轨道动力学为基础，在热力学领域内计算飞行器复杂外结构的环境热流，可保证环境热流的准确性，并使数据结果更好的与热分析计算耦合，提高热分析计算的精度。

环境热流求解过程中，辐射传递计算采用的方法通常有角系数法［1］和蒙特卡罗法［2－3］，由于需考虑飞行器表面辐射特性、表面间的多次反射和相互遮挡等问题，所以计算主要以蒙特卡罗法为主［4］。同时，在采用蒙特卡罗法的基础上，为了更合理的对热流进行统计，赵立新采用了“假想地球等效面”思想对地球红外热流进行统计［5］，安敏杰等利用了“太阳窗口”概念对空间对接结构的太阳热流进行分析［6］。

空间飞行器复杂外结构主要有以下特点:结构众多、空间位置复杂、设备尺寸差异大、表面辐射特性多样，这些因素增加了飞行器环境热流准确计算的难度。本文采用环境映射面结构对空间飞行器进行包覆后，根据飞行器的轨道特性，利用矢量转换和矢量点积等方法确定不同时刻映射面接收环境热流的大小及方向，然后通过求解映射面与飞行器表面间的辐射传递因子，最终得到飞行器表面的环境热流。该方法的优势在于具有一定的通用性，并在求解辐射传递过程中考虑飞行器表面的镜、漫射特性，结构间的遮挡及多次反射问题。计算中采用发射能束份额修正、正反蒙特卡罗法及双向统计等改进措施［7－8］，解决飞行器结构中不同设备尺寸差异大等问题。

1 轨道计算方法

对于空间运行的飞行器，了解其轨道六要素即可确定轨道面位置及飞行器的空间位置。六要素包括:飞行器轨道面对地球赤道面的倾角i;由春分点到升交点的地心角距αΩ;飞行器轨道半长轴a;飞行器轨道偏心率e;升交点到轨道近地点角距ω;飞行器通过近地点时刻τp。

以地球为中心，图1给出黄道面，地球赤道及轨道面的空间位置关系。图中，坐标系XYZ为地球赤道坐标系，XeYeZe为太阳黄道面坐标系，X0Y0Z0为飞行器轨道坐标系。

2 环境映射面

环境映射面的设计原理:映射面对于外部投射的环境热流全部吸收，并记录其投射位置、方向和大小。映射面本身并不积累能量，而是在映射面内表面与飞行器结构外表面组成的封闭系统中，按同样的位置、方向及大小进行辐射换热模拟计算，以此得到飞行器外表面环境热流。由映射面组成的封闭系统形状依飞行器外部结构形状而定，以图2为例，映射面封闭系统为长方体结构。为了避免在计算映射面的热流时考虑遮挡等影响因素，环境映射面多以平面或圆面为主。

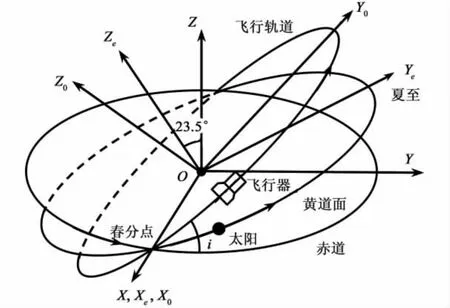
图1 黄道面、赤道及飞行轨道关系图Fig.1 The relationship among the ecliptic plane，the equator plane and orbit plane

在确定了飞行器的轨道六要素后，根据飞行器的瞬时位置，可确定飞行器外部映射面上的热流大小及方向。图3中，随着飞行器位置的变化，计算中需了解轨道坐标系 X0Y0Z0、飞行器初始坐标系X1Y1Z1及瞬时坐标系XrYrZr之间的转换关系。下面主要针对太阳辐射热流、地球红外及地球反照热流的计算进行介绍。

图2 环境映射面结构Fig.2 The structure of mapping plane with environment

2. 1 太阳投射方向的推导

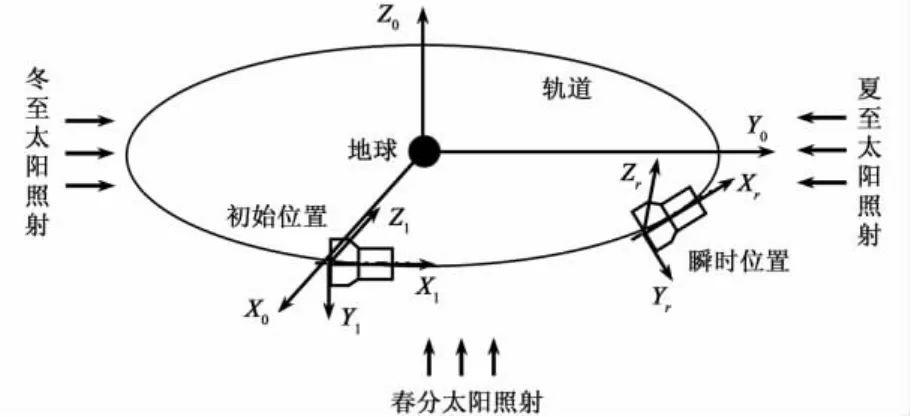
图3 飞行器瞬时位置及受照示意图Fig.3 Schematic for illuminated spacecraft

在图3所示的三个坐标系中，太阳光矢量→■S是在轨道坐标系OX0Y0Z0描述的，而飞行器结构是在瞬时坐标系OXrYrZr中描述的，所以需通过矢量坐标转换及乘积的方法，将二者在同一坐标系内表达，再进行相关计算。假设飞行器的瞬时坐标系为三轴稳定，经过τ时刻坐标系旋转的角度为θ=πτ/2T。则经过τ时刻，则飞行器的瞬时坐标系(OXrYrZr)与飞行器初始坐标系(OX1Y1Z1)的转换矩阵T1为:

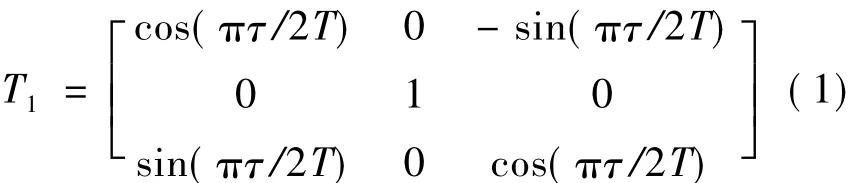
由图3知，飞行器初始时刻坐标系(OX1Y1Z1)到轨道坐标系(OX0Y0Z0)的转换矩阵T2为:

至此，可计算出飞行器瞬时坐标系中，太阳光矢量与三坐标轴间的夹角余弦，即确定了太阳矢量在飞行器瞬时坐标系中的表达式。

2. 2 环境映射面热流计算实例

环境热流的统计计算中，以太阳投射方向较难确定，尤其针对转移轨道飞行器。在前述的理论基础上，举例说明环境映射面的各热流统计。

2.2.1 太阳辐射热流

映射面结构及轨道特性如图2与图3所示，在计算各映射面的太阳辐射热流前，需首先判断太阳光能否直接照射在该映射面上，判断依据为太阳光矢量与各面法线夹角应大于90°，小于等于180°。

下面以映射面1为例，列出其表面的太阳辐射热流计算公式。该面的法向量为(0 0 －1)，太阳光在动态坐标系中的夹角余弦已由前式求得，为(cosϑ1，cosϑ2，cosϑ3)，则太阳光与面1 夹角的法向余弦为:

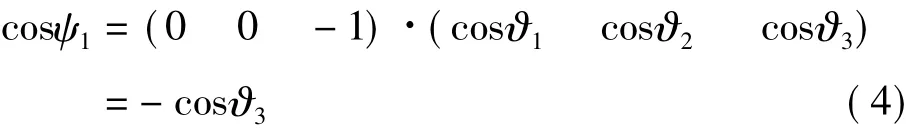
映射面1接收的太阳辐射热流表达式为:

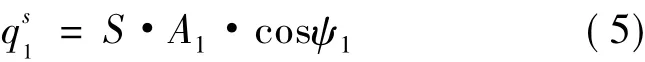
式中，S为太阳辐射常数，1353W/m2;A1为映射面1的面积，m2。

2.2.2 地球反照及地球红外热流

相比于太阳辐射热流的计算，映射面上的地球反照太阳及地球红外热流计算要简单一些。下面将以文献［9］为参考，提出本文的处理方法。

假设飞行器飞行过程中三轴稳定，+X轴指向飞行器飞行方向，+Z轴始终指向地心。则计算中仅需考虑映射面3(与地球相对的虚拟面)所接受的地球红外辐射及地球反照热流即可。

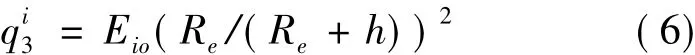
式中，Eio为将地球作为250K黑体时辐射强度，值为220W/m2，Re为地球半径，值为6370km，h为飞行器高度。

地球反照太阳辐射热流记为:

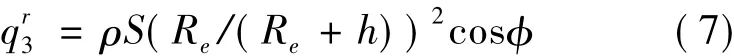
式中，ρ为地球反照率，取为0.35，φ为日地连线与微元面与地心连线夹角。

无论是地球自身红外辐射还是地球反照太阳，映射面3发射光束的天顶角均有限制，设其最大角度为θ，则:

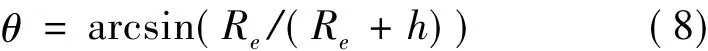
3 辐射传递因子计算

映射面结构中各面的辐射热流大小及方向统计完成后，采用蒙特卡罗法计算各映射面与飞行器设备表面组成的封闭系统中各面间的辐射传递因子，最终获得飞行器不同位置表面处的轨道外热流。

计算中，引入双向反射分布函数(BRDF)来考虑飞行器结构表面的镜、漫反射特性［10］。

式(9)定义为:在波长λ下，由(θi，Ψi)投射的光束在(θr，Ψr)方向上引起的光谱辐射强度与投射光谱能量之比。另外，Ωi投射立体角，T为表面温度。

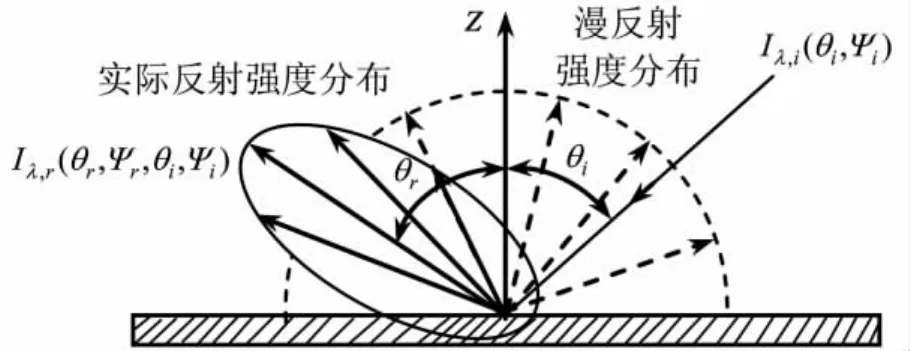
图4 双射反射分布函数Fig.4 Bidirectional reflectance distribution function

计算中考虑发射能束的方向性，以图5所示的飞行器结构为例，在外表面环境热流计算中，设备表面间的遮挡及多次反射现象明显，且部分环境热流通过开口处进入飞行器内部。在由映射面结构与设备表面形成的封闭系统内，太阳辐射模拟能束以一定方向发射，利用自动搜索功能完成能束在各表面间传递，避免因外结构复杂为计算带来的困难。图中，①线代表了蒙特卡罗法计算中，能束在设备表面间的多次反射情况;② 线代表了部分计算中，能束在飞行器内部传递情况;③线代表了部分区域由于结构遮挡，接收不到辐射热流的情况;④ 线代表地球反照及红外能束在模拟过程中，其发射天顶角需保证在θ范围内。

复杂飞行器外结构中，不同设备间的尺寸差距大，而个别较小设备又是热分析中比较重视的部分，如飞行器外部直径为0.6mm的管路。为了提高其计算精度，在环境热流计算中，可以在能束发射过程中，单独提高该类设备表面的抽样密度，并通过改进的蒙特卡罗法进行统计计算，以达到精确求解目的。

4 算例及结果分析

根据上述介绍的环境热流计算方法，仍以图5所示的飞行器外结构为例，分析其不同表面的热流计算结果，结果如图6。图中曲线1、曲线2和曲线3所对应的位置在图5中已有标识。

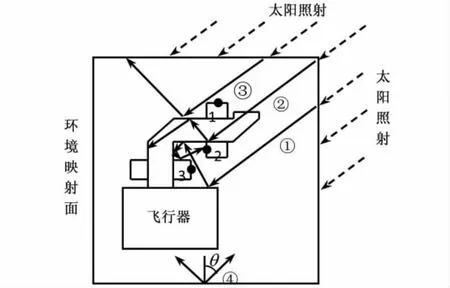
图5 映射面与飞行器表面间辐射传递Fig.5 Radiation transfer between mapping plane and surfaces of spacecraft

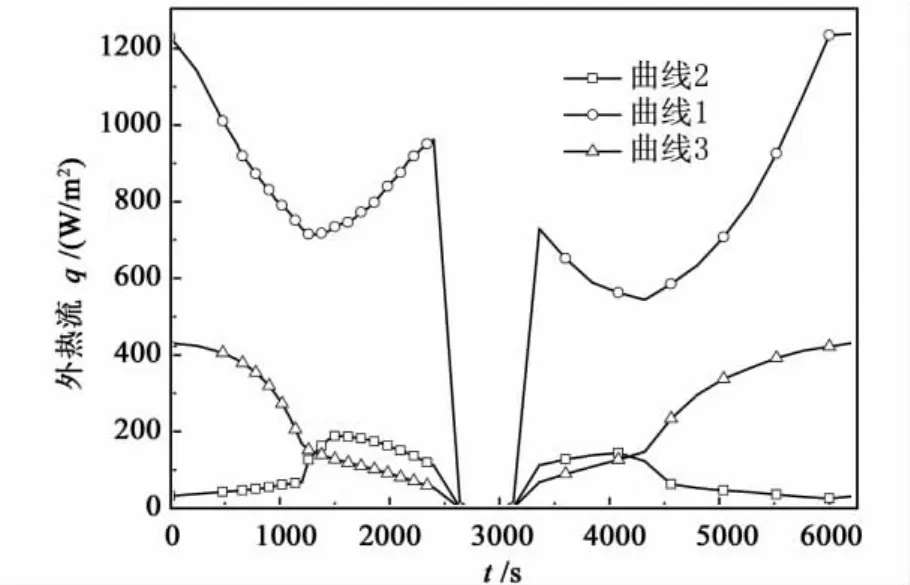
图6 部分位置外热流Fig.6 Heat flux for some surfaces

图6 中，飞行器在3000s附近需经过阴影区，此时不存在环境热流。由图5的太阳照射方向可知，位置1是最容易受到太阳照射的，所以在飞行周期内其外热流均保持较高的值。对于位置3，由于在部分情况下存在遮挡，所以其表面热流波动较大。而对于位置2，在多数情况下，其表面热流仅能通过飞行器其它表面的反射才能得到，所以整体热流值较低。另外，由于飞行器的部分结构存在转动情况，造成飞行周期内各表面的热流值呈非规律性变化。

5 结论

针对空间飞行器复杂外结构，各种因素给精确计算其表面的环境热流带来困难。本文引入环境映射面的概念，并与蒙特卡罗法结合，提出了一种较通用的环境热流计算方法。环境映射面的引入为辐射热流的统计带来方便，并为蒙特卡罗法的实施提供支持。计算中考虑了复杂结构下飞行器表面辐射特性不同，相互遮挡及多次反射问题。同时，蒙特卡罗法中发射能束份额修正、正反蒙特卡罗法及双向统计等改进措施可为复杂结构的环境热流计算提供帮助。

［1］ O’Neill R F，Lorentz D R.A vector approach to numerical computation of view factors and application to space heating［J］.AIAA，1983，1－5.

［2］ Howell J R.The monte carlo method in radiative heat transfer［J］.Journal of Heat Transfer，1998，120:547 －560.

［3］ Howell JR，Perlmutter M.Monte carlo solution of thermal transfer trough radiant media between gray walls［J］.Journal of Heat Transfer，1964，86(1):547 －560.

［4］ 翁建华，潘增富，闵桂荣.镜反射凹面及相互可视表面的轨道外热流计算［J］.中国空间科学技术，1994，4:7－14.［Weng Jian-hua，Pan Zeng-fu.Calculating orbital heat fluxes of concave surfaces and mutually visible surfaces with specular reflection［J］.Chinese Space Science and Technology，1994，4:7－14.］

［5］ 赵立新.Monte-Carlo法在空间外热流计算中的应用—空间光学遥感器光学窗口的地球红外辐射分析计算［J］.光学精密工程，1995，3(6):71－79.［Zhao Li-xin.Earth infrared radiation analysis and calculation for the optical window of high resolution space optical remote senser［J］.Optics and Precision Engineering，1995，3(6):71 －79.］

［6］ 安敏杰，程惠尔，李鹏.空间对接机构太阳外热流的计算与分析［J］.上海航天，2006，1:22－26.［An Min-jie，Cheng Hui-er，Li Peng.Computation and analysis of solar external heat flux in the docking mechanism［J］.Aerospace Shanghai，2006，1:22 －26.］

［7］ 夏新林.空间光学系统的杂散辐射计算与热分析研究［D］.哈尔滨工业大学博士学位论文，1997.［Xia Xin-lin.A study of the stray radiation calculation and thermal analysis for spaceborne optical systems［D］.Harbin Institute of Technology，1997:1 －11.］

［8］ 夏新林，任德鹏，郭亮.求解介质内热辐射传递的双向统计蒙特卡罗法［J］.工程热物理学报，2006，27(2):21－24.［Xia Xin-lin，Ren De-peng，Guo liang.Bidirectionally statistical monte carlo method for radiative heta transfer in medium［J］.Journal of Engineering Thermophysics，2006，27(2):21 －24.］

［9］ 闵桂荣，郭舜.航天器热控制(第二版)［M］.北京:科学出版社，1998.［Min Gui-rong，Guo Shun.Spacecraft thermal control［M］.Second Edition.Beijing:Science Press，1998.］

［10］ 谈和平，夏新林，刘林华，等.红外辐射特性与传输的数值计算—计算热辐射学［M］.哈尔滨:哈尔滨工业大学出版社，2006.［Tan He-ping，Xia Xin-lin，Liu Lin-hua，et al.Numerical calculation of infrared radiative transfer［M］.Harbin Press of Harbin Institute of Technology，2006.］