焊球点不同分布模式下的焊球数量的解析模型研究

晏 江,万建武,余 龙

广州大学,广东广州510006

焊球点不同分布模式下的焊球数量的解析模型研究

晏 江,万建武,余 龙

广州大学,广东广州510006

在数据统计的基础上,对倒装芯片焊球采用叉排布置时,焊球数量的变化情况进行了分析研究,提出了相应的解析分析模型,并对所提出的解析分析模型的可靠性进行了验证.研究结果表明,所得出的解析方程式的计算结果与实际数据能很好地吻合.

倒装芯片;焊球顺排;焊球叉排;解析模型

在倒装芯片的封装方式中,焊球点是连接芯片和基板的通道.相同尺寸芯片上布置的焊球点越多,意味着芯片具有更高的信号输出输入能力.当前焊球的分布模式主要采用顺排排列方式,为了在一定程度上增加芯片的输入输出(I/O)容量,叉排排列方式在一定条件下是一种可行的焊球分布模式.目前,在这两种排列方式下,焊球点的数量变化情况尚处于数据统计及一些简单的计算阶段,缺乏理论方面的分析.本文在数据统计的基础上,对焊球点的数据统计做出详细的解析分析,提出了相应的解析分析模型.

1 焊球分布的数据统计

在芯片面积和相邻焊球点中心距离相同的情况下,如果叉排布置的焊球点比顺排的多,这说明在芯片面积相同的情况下,焊球点采用叉排布置芯片会有更高的信号输出输入能力.本文在参考文献[4]的工作基础上,取两种不同的焊球布置情况进行分析,相关统计数据分别列于表1和表2.表1的焊球直径为168μm,焊球间中心距离为262μm.当焊球点为顺排方式时,芯片边缘与焊球点边缘之间的缝隙宽度为0.122 mm,叉排时右边芯片边缘与焊球点边缘之间的缝隙宽度不小于0.122 mm.表2的焊球直径为100μm,焊球间中心距离为250μm.当焊球点为顺排方式时,芯片边缘与焊球点边缘之间的缝隙宽度为0.075 mm,叉排时右边芯片边缘与焊球点边缘之间的缝隙宽度不小于0.075mm.

表1 直径为168μm焊球不同布置的统计结果Table 1 Statistical results of solder bump of 168μm in diameter under different distribution patterns

(续表1)

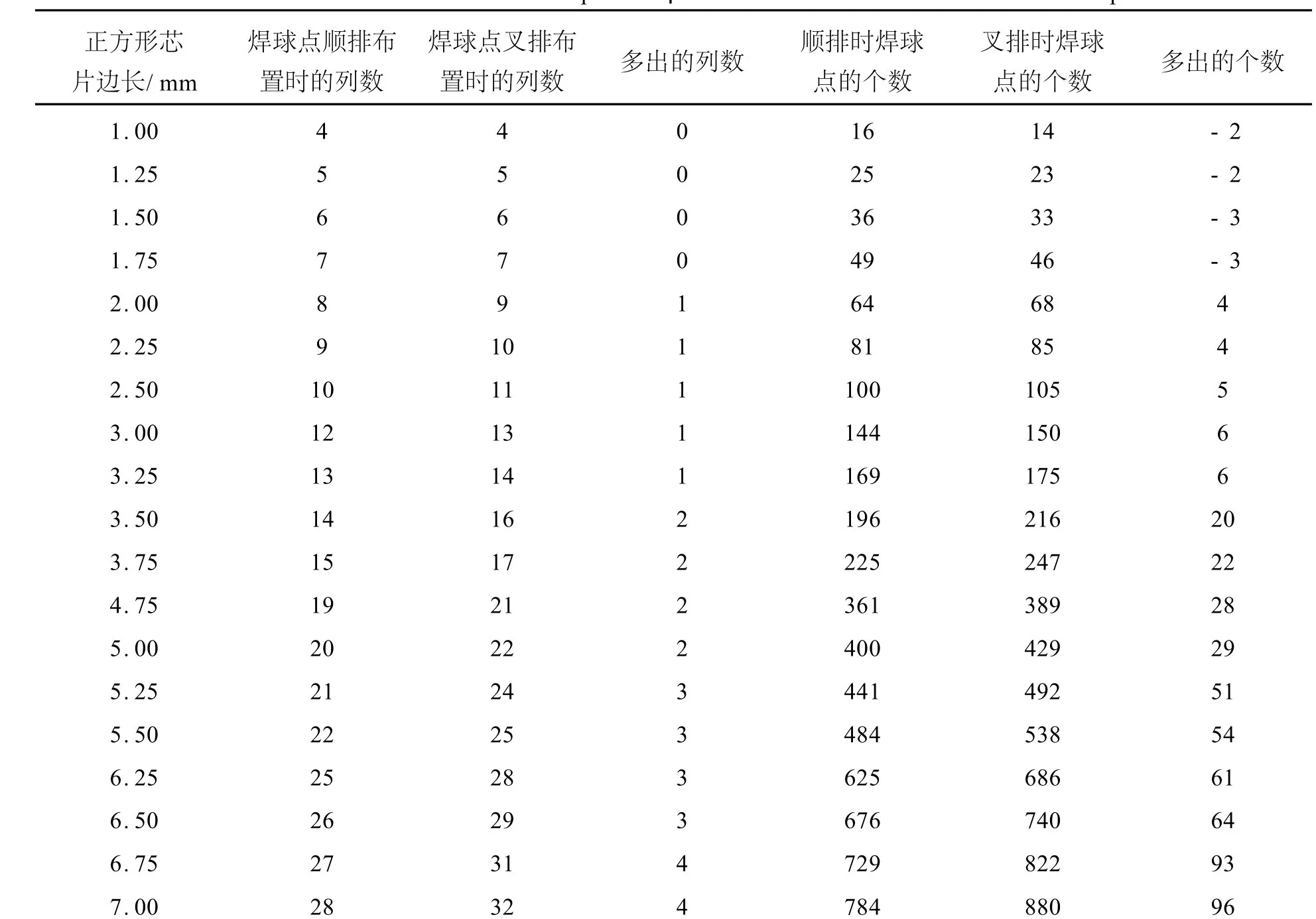
表2 直径为100μm焊球不同布置的统计结果Table 2 Statistical results of solder bump of 100μm in diameter under different distribution patterns

从表1和表2的统计数据可以看出:随着芯片面积的不断变大,采用焊球点叉排布置方式,确实能够布置更多的焊球点,这样能提高芯片的信息输入输出能力;焊球点的增多与叉排布置时列数的变化有着密切的关系,而且列数的增加具有一定的规律.由此可知,在数据统计的基础上,做出相应的解析分析是很有必要的.

2 焊球叉排布置方式的解析分析

2.1 叉排排数变化的解析分析

为了方便计算,特将叉排布置中的焊球数量比相邻列较少的焊球列向上平移至与第一行对齐,即将图1(b)中的第2和4列向上平移个单位 ,使之变成图1(c).当焊球叉排布置时,与顺排相比行列均发生了变化,但焊球的布置情况又不能同时满足各行各列焊球布置的饱满度.经过图1(c)的变换后可以做出如此假设,即当焊球叉排布置时,焊球的行数没有发生变化,即和焊球顺排布置时的行数是一样的,仅仅是焊球的列数发生了变化,并且根据以上的假设满足排数 m1=m2和边长 l1=l2.从图1(c)可见,经变化后的焊球排列的行数和行距没有发生变化,只是第2列和第4列的焊球比其他列的焊球少一个,即偶数列的焊球要比奇数列的焊球少一个.

以下各式中所涉及到的字母为图1中相对应的参数,其中1代表顺排布置,2代表叉排布置;c表示顺排布置时,行列方向的边缘缝隙,同时也表示叉排布置时除右边边缘外的其他边缘的边缘缝隙;c2表示叉排布置时,芯片右边边缘的边缘缝隙.

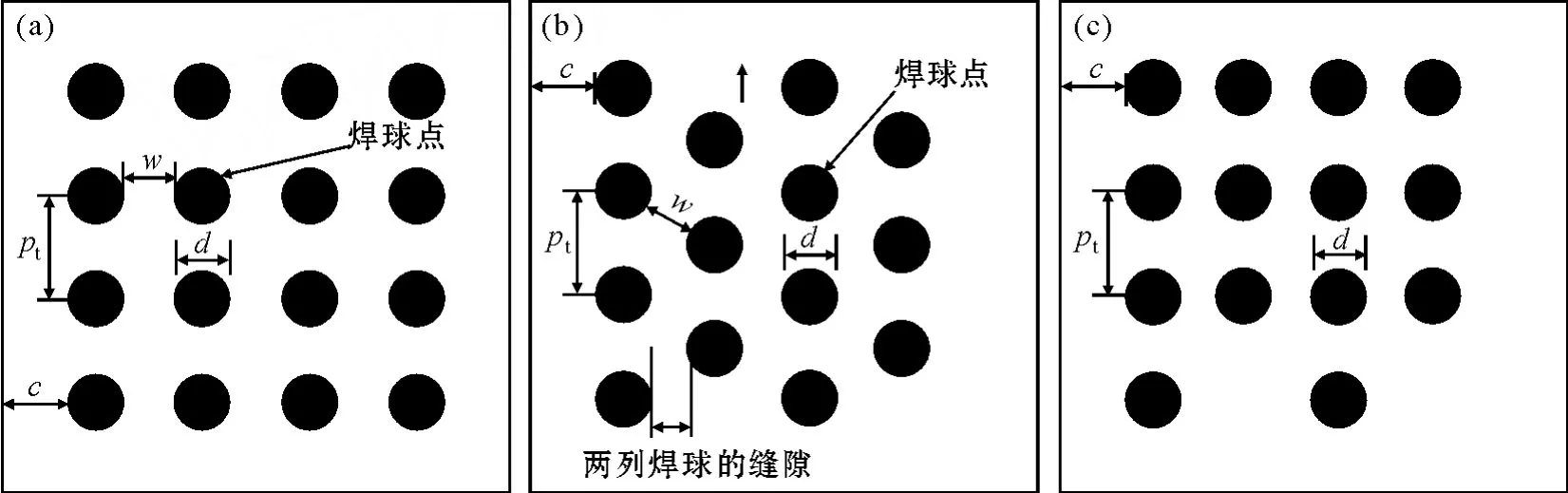
图1 焊球布置参数(a)顺排布置;(b)叉排布置;(c)变换后的布置Fig.1 Parameters of solder bumps arrangement(a)tandem arrangement;(b)stagger arrangement;(c)arrangement after transfo rm

由于芯片是正方形芯片,在进行排列布置焊球时,是按照顺排布置模式进行比较的,也就是说,叉排布置时焊球的行数是一定的,其长度即为芯片的边长.经计算可得:

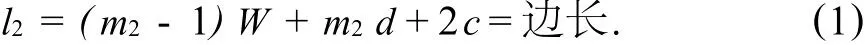
列方向上的计算方式,与行方向上的计算稍有区别,但是芯片是固定的,所以其计算出的结果不变,表达式为:

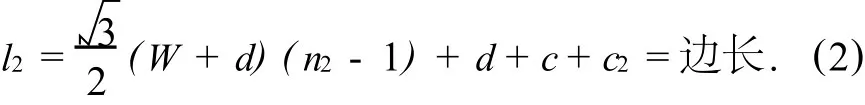
在叉排布置中相邻两焊球是以等边三角形的模式布置的,故相邻两焊球的水平间距d),即图1(c)中的相邻两列的中心距为比顺排排列(图1(a))时焊球的间距缩短,缩短的长度为:

由于焊球间水平距离的缩短,随着列数增加到一定的程度,以及Δpt的不断累积,叉排排列的列数会比顺排的增多.为使叉排布置时的焊球列数增加1列,所需的顺排布置的列数为 n1,则有:

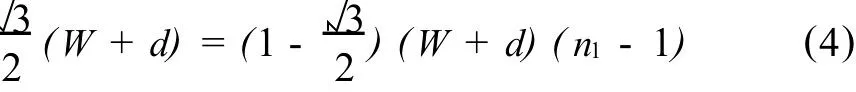
其中n1-1表示相邻两列焊球的中心距数,经计算得出n1-1=2+3≈6.646,由此所得出 n1至少为7.464,故 n1的最小值应取8,而此时叉排布置的列数比顺排布置时的列数增加了1列.当芯片的长度大于或等于 l1=7(W+d)+2c+d时,可使叉排布置时的焊球列数增加,从而增加焊球布置的数量,提高芯片的输入输出容量.

同理,若想叉排布置的列数比同样情况下的顺排布置的列数增加 a列,则有:

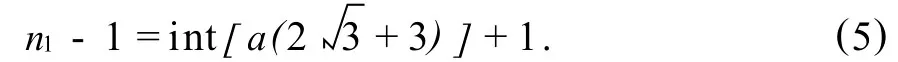
式(5)中int为取整函数.此时焊球叉排布置时的列数比顺排布置时多出 a列,通过式(4)计算出的 a与a+1顺排的列数值用 na和na+1表示,则顺排布置时介于这两个值之间的任何顺排的列数值,都能够使同种情况下叉排布置时的列数多出a列.

2.2 焊球点数量变化的解析分析

在计算叉排布置的焊球的数量时,已知排列的列数为 n2,则排数为 m2的计算公式如下:

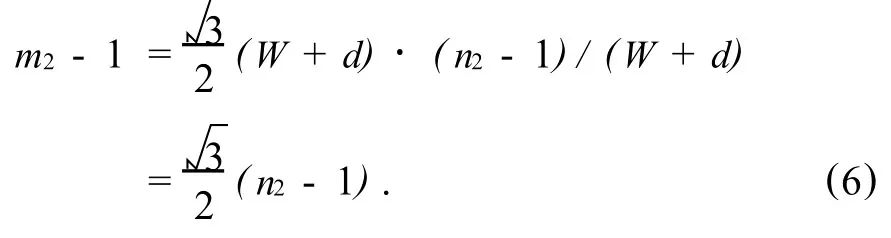
由于芯片是正方形芯片,在进行排列布置焊球的时候,是按照顺排布置模式进行比较的,也就是说,叉排布置时焊球的行数是一定的,其长度 l2,即为顺排布置时芯片的边长,与列数方向的式(2)进行比较,则有c=c2,显然这个结论是不成立的.因为涉及到这个无限不循环小数,在满足行数方向正常排列的情况下,列数方向是不可能恰好布置的,此时的c2应该略大于c,但又不能满足足够的空间使焊球列数增加,所以由式(6)可知,当 m2-1取整时,应该取比(n-1)大的最小整数,所以有:2

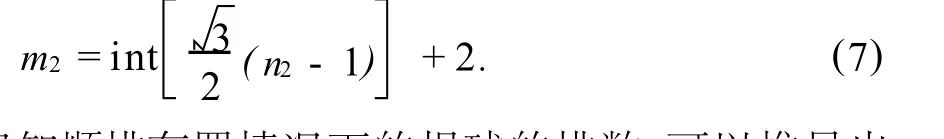
若已知顺排布置情况下的焊球的排数,可以推导出相对应叉排布置时焊球布置的列数,即:

顺排布置时,焊球的数量:

叉排布置时,焊球的数量为奇数和偶数时,方程式分别为:

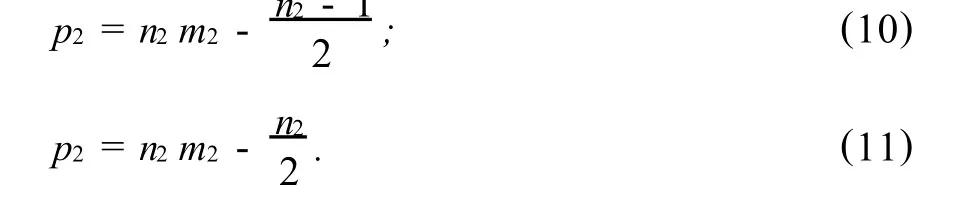
3 解析分析模型的验证

表3为解析分析模型的计算结果与表2中有关数据的比较.表3可知,所提出的解析分析模型的计算结果与实际的结果相符合.表明,解析分析模型是可靠的.

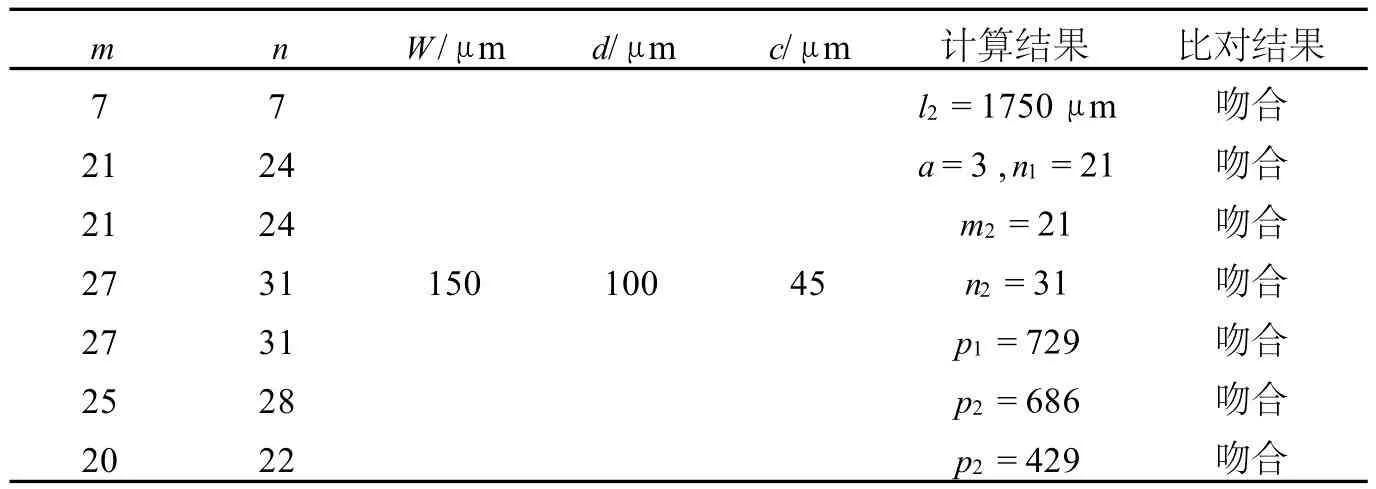
表3 数据结果比对Table 3 Comparison of data results

4 结 论

所提出的解析方程式的计算结果与实际数据能很好地吻合,在顺排和叉排布置情况下,能方便地计算出焊球的数量及列数,从而确定哪种方式下焊球的数量较多,为芯片提供更大的数据输入输出能力.

[1]谯凯.M EMS器件倒装芯片封装中的柔性化凸点制备技术及其应用[D].武汉:华中科技大学,2001.

[2]WAN JW,ZHANGW J,BERGSTROM D.An analyticalmodel fo r p redicting the underfill flow characteristics in flip-chip encapsulation[J].IEEE Transactions on Advanced Packaging,2005,28(2):481-487.

[3]万建武.倒装芯片封装的下填充流动研究[M].北京:科学出版社,2008:103-106.

[4]张良明,万建武.焊球分布模式对芯片下填充胶流动的影响[J].电子工艺技术,2008,29:3.

Study on analyticalmodel of solder-bump number under different distribution patterns

YAN Jiang,WAN Jianw u,YU Long
Guangzhou University,Guangzhou 510006,China

In this paper,on the basisof statistical data,through the analysisof solder-bump number in staggered arrangement of flip-chip package,an analyticalmodel is p roposed,and the reliability of the model is also validated in thispaper.The results show that the analytical equation can bewell in agreementw ith the actual data.

flip-chip;aligned arrangement;staggered arrangement;analyticalmodel

TF123.121

A

1673-9981(2011)02-0125-05

2010-11-22

晏江(1986—),男,湖北应城人,硕士研究生.