关于DEA模型应用过程中滞后问题的探讨

吴 敏，管 艳

（河海大学 商学院，南京 210000；南京航空航天大学 工商管理学院，南京 210000）

关于DEA模型应用过程中滞后问题的探讨

吴 敏，管 艳

（河海大学 商学院，南京 210000；南京航空航天大学 工商管理学院，南京 210000）

DEA在评价社会经济系统相对有效性时具有绝对的优势，目前已成为评价科技资源投入产出效率问题普遍使用的方法之一。然而，在运用DEA模型评价科技资源投入产出效率的过程中，科技投入资源对科技产出资源的滞后影响往往被忽略。文章以江苏省1996～2005年的科技资源的投入产出数据为基本数据源，在假设检验的基础上，提出了解决存在产出滞后因素的改进DEA方法，为解决滞后性的定量测度作出了进一步的尝试。

DEA模型；科技资源；滞后长度；滞后影响系数；假设检验

0 引言

自从1978年著名运筹学家A.Charnes和W.W.Cooper提出第一个DEA模型以来，DEA方法不断得到完善并在实际中被广泛运用，诸如被运用到技术进步、技术创新、资源配置、金融投资等各个领域。现在有关的理论研究不断深入，应用领域日益广泛。应用DEA方法对社会经济系统多投入和多产出相对有效性评价，是独具优势的[1]。随着经济的发展，科学技术的重要性越来越凸显出来，各国不断加大对科技资源的投入。如此科技资源投入产出效率的评价问题就引起越来越多的讨论。DEA方法独特的优越性决定了该方法是目前评价科技资源投入产出效率问题普遍使用的方法之一[2～5]。

然而科技产出相对于科技投入的滞后性是客观存在的。上述文献在评价的过程中或者没有考虑滞后性的问题，或者认为科技产出滞后于科技投入一年，但是事实上科技产出相对于科技投入的滞后性不止表现在某一年，而是若干年。针对这些问题，本文将以江苏省1996～2005年的科技资源的投入产出数据为基本数据源，提出解决存在产出滞后因素的改进DEA方法，试图为解决滞后性的定量测度作出进一步的尝试。

1 评价指标的设计

用定性方法确定评价指标不可避免地会给评价结果带来偏差，因此本文首先将江苏科技统计年鉴中各市科技进步监测指标体系作为待选指标集，然后采用相关分析来选取科技投入和产出指标。

设有 p个待选指标 x1,x2,…,xp，其n个样本值用 xij表示(i=1,2,…,p;j=1,2,…,n)。 以(x11,x12,…,x1n),(x21,x22,…,x2n),…,(xp1,xp2,…,xpn)表示p个变量的一组样本观测值，这里(xi1,xi2,…,xin)表示第i个变量的容量为n的一组样本值(i=1,2,…,p)，则有样本相关矩阵RX。为体现投入指标之间的相对独立性，根据相关系数的大小，剔除相关性较大的指标来确定投入指标。同理计算出产出指标样本的相关矩阵RY。为体现产出的集中度，根据相关系数的大小，剔除相关性较小的指标，从而确定产出指标。

投入指标：I1为每万人口中科技人员数 （人/万人）；I2为R&D人员占科技活动人员的比重 （%）；I3为R&D支出占国内生产总值比重（%）；I4为科技拨款占财政支出的比重（%）。

产出指标：O1为专利授权量（件）；O2为高技术产业销售收入（亿元）。

2 DEA模型的改进

要进行科学地评价科技资源的投入产出效率，首先必须确定各个科技产出指标相对于科技投入的滞后长度，然后确定每一期的科技投入指标对本期科技产出指标的影响系数（以后也称作滞后影响系数）以及对之后的一期或几期产出指标的滞后影响系数。因此本文先对滞后长度和滞后影响系数的确定方法进行初探，在此基础上对DEA模型进行改进。

2.1 滞后长度的计算

有的文献提出利用修正判定系数R2大小来确定各个科技产出指标相对于科技投入的滞后长度，消除了用定性方法确定滞后长度的弊端。但是考虑到复相关系数R比修正判定系数R2具有更明确的经济含义，本文选用复相关系数R来确定滞后长度。由于相同滞后期的复相关系数R在各个时期的大小不等，因而需对不同时期的复相关系数大小进行比较检验。

首先计算1996～2005年滞后0期～滞后6期 （考虑到实际情况与数据的可获得性，滞后6期以后的数据不再考虑）的江苏省科技产出资源与当期投入之间的复相关系数R，鉴于篇幅本文只给出专利授权量这一产出指标数据的计算结果。见表1。

表1 1996～2005年滞后1～6期专利授权量与当期投入之间的复相关系数R

表2 1996～2005年滞后1～6期专利授权量与当期投入的复相关系数R的假设检验

由此可知，在显著性水平为15%的条件下，各期的产出指标专利授权量与当期的投入指标之间的总体相关系数不为0，而在复相关系数不为0的情况下，复相关系数之差不服从正态分布，也不服从T分布。故相关系数之差不服从正态分布，也不服从T分布。为了满足假设检验的基本条件，故需要对以上计算所得的相关系数进行fisher转换 （鉴于篇幅计算结果不再给出）；转换后的数据服从正态分布，因而可以对其进行T检验。将滞后0期～滞后6期的fisher转换后的复相关系数进行两两配对计算均值之差，然后对均值之差进行假设检验。因总体方差未知及考虑的样本是小样本，故假设检验采用T检验法，以表2第一行的数据为例，检验的原假设为滞后0期的专利授权量与当期投入的复相关系数值小于或等于滞后1期的专利授权量与当期投入的复相关系数值，经计算其单侧检验值为13.80%，因而在显著性水平为15%的条件下我们拒绝原假设，认为滞后0期的专利授权量与当期投入的复相关系数值大于滞后1期的专利授权量与当期投入的复相关系数值。依据以上分析可以看出，在显著性水平为15%的条件下滞后0期和滞后1期的复相关系数比其他滞后期的复相关系数大，因此我们有理由相信江苏省四个科技投入指标相对于专利授权量的滞后长度为1，滞后期为0和1。同理可以得出在显著性水平为15%的条件下滞后0期和滞后1期的复相关系数比其他滞后期的复相关系数大（鉴于篇幅计算结果不再给出）。因此，也有理由相信江苏省四个科技投入指标相对于技术产业销售收入的滞后长度为1，滞后期为0和1。

2.2 滞后影响系数的确定

为了引出滞后影响因素的测算我们只考虑存在一种科技投入（I）和一种科技产出（O）的决策单元，共有n期的生产过程，如果每期的科技投入只影响本期的科技产出，即不考虑科技产出的滞后影响；但现在考虑当期科技投入不仅对当期的产出有影响而且对下一期的产出有影响的情况，即滞后长度为1，如图1所示。

首先，从投入的角度看，每一期的投入均对本期的科技产出产生影响，本文把这种影响分别用系数α、β来表示，并且使用下标表示α、β所属的科技投入的期数。如α1表示第1期的科技投入对第1期的科技产出的影响，β1表示第1期的科技投入对第2期的科技产出的影响，因此第1期的投入I1的实际产出LO1为α1O1+β1O2；类似可得出第2期的投入I2的实际产出LO2为α2O2+β2O3，同理可以推出一般的结论，第k 期的投入 Ik的实际产出 LOk为 αkOk+βkOk+1（k=1，2，……，n-1），这里第n期的投入不能被评价，因为没有给出第n+1期的产出值。其次，从产出的角度看，各期的科技产出一部分是由本期的科技投入所产生的，另外一部分是由上一期的科技投入所产生的，如O2是由α2O2和β1O2组成的，从而可以得出 α2+β1=1； 同理可以推出一般的结论，αk+βk-1=1 （k=2，3，……，n），这里第1期的上一期的投入未知因此上一期对该期的滞后影响系数不能确定。如果滞后长度增加，只需按照同样的方法增加滞后影响系数即可。

考虑到之后影响系数的计算需要和DEA模型保持一定的兼容性，本文尝试考虑按以下方法来计算之后影响系数：首先利用经典的CCR模型计算出各决策单元在各个科技产出指标和对应各期投入所组成指标体系下的效率值；然后以该各期的效率值为数据集利用熵权法计算权重，则所计算的权重可作为滞后影响系数。如若考虑产出O2经检验滞后0期和1期比较显著，那么产出O2与投入I1作为指标体系可计算出一组效率值，产出O2与投入I2作为指标体系也可计算出一组效率值，这两组效率值组成的矩阵作为基本数据集利用熵权法计算出各自的权重，即可以认为所求的滞后影响系数 α2和 β1。

表3 1996～2005年科技投入对2个产出指标的滞后影响系数

按照此方法可计算出1996～2005年科技投入对2个产出指标的滞后影响系数如表3所示，这8年①不考虑1996年和2005年，因为1996年无法计算当期影响系数，2005年无法计算滞后1期的影响系数。里有7年的科技投入对滞后0期的专利授权量的影响系数大于对滞后1期的专利授权量的滞后影响系数，同时也有7年的科技投入对滞后0期的高技术产业销售收入的影响系数大于对滞后1期的高技术产业销售收入的滞后影响系数；由表3还可以看出在显著性水平15%之内，滞后0期的专利授权量与投入指标的相关性比滞后1期的大，滞后0期的高技术产业销售收入与投入指标的相关性比滞后1期的大，因此按此方法计算出的权重与上面假设检验的结果是相吻合的，从而说明用该方法的可行性。

2.3 改进的DEA模型

在完成各期科技投入指标对产出指标对应的滞后影响系数的测度之后，便可以计算出各期的科技投入所产生的实际产出，将实际产出值代替原来各经典DEA模型中的产出值便得到相应的改进DEA模型。假设对于科技产出相对于第t期的科技投入的滞后长度为K，则其各个实际产出指标值为，以下给出具有阿基米德无穷小的经典CCR模型的改进形式如式（1）。

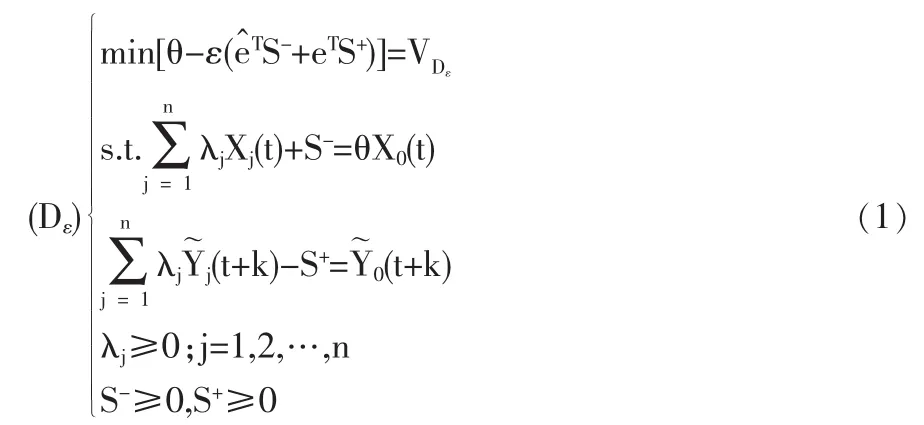
对江苏省科技投入产出资源数据的计算可知K为1，1997～2004年专利授权量的实际值分别为0.4856Y1997专+0.4271Y1998专；0.5729Y1998专+0.5057Y1999专，0.4943Y1999专+0.4763Y2000专；0.5237Y2000专+0.4496Y2001专；0.5504Y2001专+0.4717Y2002专；0.5283*Y2002专+0.4468Y2003专；0.5532*Y2003专+0.5271Y2004专；0.4729Y2004专+0.4880Y2005专。 1997～2004 年高技术产业销售收入的实际值分别为0.4703Y1997高+0.4216Y1998高；0.5784Y1998高+0.5223Y1999高；0.4777Y1999高+0.5152Y2000高；0.4848Y2000高+0.3925Y2001高；0.6075Y2001高+0.5020Y2002高；0.4980Y2002高+0.4689Y2003高；0.5311Y2003高+0.4436Y2004高；0.5564Y2004高+0.5254Y2005高。 其中 Y1997专表示 1997年专利授权量的指标值，Y1997高表示1997年高技术产业销售收入的指标值，其余依次类推。将各个实际的产出指标值代替原产出指标值代入DEA模型中即得到改进的DEA模型，这样可得到综合考虑滞后影响因素的效率值，在一定程度上使得整个评价过程更符合实际。

3 结论

本文从某种程度上来说解决了现有文献评价科技资源配置时未考虑滞后性或考虑滞后性不周所带来的问题。一方面，本文所给的改进方法是在假设检验的基础上对滞后长度进行的测度，具有客观性；另一方面，科技投入对科技产出的滞后影响系数是从效率的角度并结合熵权法计算而得到，在保证客观性的基础上同时也保证了兼容性。但滞后长度和滞后影响因素的测度只能是一个不断完善、逐渐逼近的过程，尚须完善直至找到一个更好的视角或方法。

[1]杜栋,庞庆华.现代综合评价方法与案例精选[M].北京：清华大学出版社，2005.

[2]吴和成,郑垂勇.科技投入相对有效性的实证分析[J].科学管理研究,2003,21(3).

[3]孙宝凤,李建华,杨印生.运用DEA方法评价地区科技资源配置的相对有效性[J].数理统计与管理,2004,23(2).

[4]许治,师萍.基于DEA方法的我国科技投入相对效率评价[J].科学学研究,2005,(4).

[5]吴和成,刘思峰.基于改进DEA的地域R&D相对效率评价[J].研究与发展管理,2007,(2).

[6]江苏省科技情报所编.江苏科技年鉴(1997～2006)[M].北京:科学技术文献出版社,1997～2006.

F224

A

1002－6487（2011）10－0029-03

吴 敏（1985-），女，江苏南京人，博士研究生，研究方向：管理科学与工程。

（责任编辑/亦 民）