基于GMDH的小样本数据预测模型

2011-12-14何跃，尹静

统计与决策 2011年10期

关键词：建模样本曲线

何跃，尹静

（四川大学工商管理学院，成都 610064）

基于GMDH的小样本数据预测模型

何跃，尹静

（四川大学工商管理学院，成都 610064）

对于样本数据少的情况，文章中利用SPSS曲线估计的方法选取三次曲线和二次曲线两种模型进行预测，同时用GMDH自回归模型进行分步预测，最后利用GMDH组合模型将三种模型进行组合预测。预测结果表明：GMDH自回归模型对于小样本数据的预测结果优于其他模型，效果更好、更稳定。

小样本数据；SPSS曲线估计；GMDH自回归模型；组合预测

0 引言

现代宏观经济预测的各种模型，如回归预测模型、马尔可夫预测模型、灰色系统预测模型、投入产出预测模型等，多是基于对已知数据的分析，找到数据内部的规律和相互依赖关系，从而得到对未知数据的预测能力。但是这是基于样本数据足够多的前提下，对于样本比较少的数据，预测效果往往不好。利用一般的宏观经济预测模型预测小样本数据一般都存在一定的缺陷。例如回归预测模型需要大量的历史数据，而多元非线性回归模型不仅建模难度大，且计算过程复杂；马尔可夫模型虽然需要的数据量小，但是计算的准确率偏低而存储复杂度偏高；灰色系统预测模型的特点是小样本建模，但模型本身还存在一定的问题[1]。

基于以上模型的缺点，学者们开始对小样本预测的进一步研究。例如安红刚等提出小样本进化神经网络预测模型对盾构施工实测位移资料样本进行建模预测下一步施工的地表变形，效果更好[2]；针对武器系统实验数据小样本建模问题，徐军辉等提出了通过二次修正插值方法解决测试数据的非等间隔性和样本容量小的问题，提高了预测精度[3]；曾波等（2009）从序列灰色关联度的角度去挖掘数据之间变化的规律，对中国2008年的GDP进行预测，预测结果显示了GIFM(m)模型具有比传统的GM(1,1)模型以及GM(1,n)模型更高的预测精度。

由上面的研究可以看出，利用进化神经网络和二次修正插值方法都是对数据进行预处理的改进，在此基础上再利用一般预测方法预测；虽然灰色关联度的预测优于传统的灰色系统预测模型的预测结果，但是误差却高达6.80%，误差相对较大。根据以上研究和工业增加值小样本数据的特点，本文将对四川省七大优势产业的工业增加值建立SPSS曲线模型，选取两个最优的模型，利用GMDH自回归模型预测，最后将三种模型进行GMDH组合预测。

1 预测模型介绍

1.1 SPSS曲线估计模型

变量之间的关系并不总表现出线性关系，非线性关系也是极为常见的。对于非线性关系，我们通常无法通过线性回归来分析，无法直接建立线性模型[4]。SPSS曲线估计模型中，在不能明确究竟哪种模型更接近样本数据的变化规律时，可以在软件界面上列出来的众多选项中选择出多种模型，如:二次曲线（Y=b0+b1t+b2t2）、复合曲线、增长曲、对数曲线(Y=b0+b11n(x))、三次曲线(Y=b0+b1xb2x2+b3x3)、s 曲线、指数曲线、逆函数曲线(Y=b0+b1/x)、幂函数曲线、逻辑函数曲线等多种模型分别来拟合样本数据，然后计算各个模型的参数，并计算回归方程显著性检验的f值和概率p值、判定系数R平方等统计量；最后，以判定系数为主要依据选择其中的最优模型，并进行预测分析等[5]。

1.2 GMDH自回归模型

1.2.1 原理介绍

自组织理论又称数据组合处理方法GMDH(Group-Method of Data Handling)，是基于神经网络和计算机科学的迅速发展而产生和发展起来的[6]。它将黑箱思想、生物神经元方法、归纳法、概率论、数理逻辑等方法有机地结合起来，实现了自动控制与模式识别理论的统一，极大减少了人在认识过程中的参与，从而更具有客观性与公正性。自组织建模思想首先由乌克兰控制论学家A·G·Ivakhnenko提出，并在Adolf Mueller等德国科学家的协作下得以不断发展，如今已成为一有效而实用的数据挖掘工具[7]。其主要思想是通过各种简单的初始输入(局部模型)的交叉组合产生第一代中间候选模型，再从第一代中间候选模型中选出最优的若干项结合而产生第二代中间候选模型，重复这样一个产生、选择和遗传进化的过程，使模型复杂度不断增加，直到选出最优复杂度模型为止[8]。

它将观测样本数据分为训练集和测试集：在训练集上利用内准则建立中间待选模型，在测试集上利用外准则进行中间候选模型的选留。当外准则达到最小时，相应的模型即为最优复杂度模型。这个模型表达了输入输出变量之间的相互关系[9]。

1.2.2 算法步骤

(1)将数据样本集(N个数据样本)分为训练集A和检测集B(Nω=NA+Nb,ω=A∪B)若建立预测模型，则将数据样本集分为学习集 A，检测集 B 和预测集 C，Nω=NA+NB,ω=A∪B∪C。

(2)建立因变量(输出)和自变量(输入)之间的一般关系，作为“参考函数”，一般常用K—G多项式。例如对于三输入单输出系统，可取二次K—G多项式

为参考函数，并以它的子项作为建模网络结构中的10个初始模型：

(3)从具有外补充性质的选择准则中选出一个(或若干个)作为目标函数(体系)，或称为外准则(体系)。

(4)产生第一层中间模型。第一层中间模型们由自组织过程自适应产生，且因所含变量个数、函数结构而彼此不同，同时在训练集A上估计参数。

(5)对第一层中间模型进行筛选。根据外准则，在检测集B上对第一层中间模型进行筛选，选出的中间模型作为网络第二层的输入变量。

(6)形成最优复杂度模型网络结构。重复（4）、（5）两步，可依次产生第二、第三…层中间模型，最终形成可用于分析的显式最优复杂度模型[10][11]。

1.3 组合预测

所谓组合预测，就是将不同的预测方法进行适当的组合，综合利用各种方法所提供的有用信息，从而尽可能的提高预测精度。2003年诺贝尔经济学奖得主、美国加利福尼亚大学的C.Granger教授关于组合预测的评价是：组合预测提供了一种简便而实用的可能产生更好预测的途径。

权系数组合预测法的特点是单模型的线性组合，而往往单个预测模型都是非线性的；非线性组合预测法所需设计的参数比大多数统计预测模型都多，有时会造成网络模型的过拟合现象，即这种模型虽然对样本数据有较高的拟合精度，但预测能力差。GMDH组合预测模型恰好能解决这些问题，它是基于样本数据自身特点进行预测，解决了这些问题。因此本文选取该方法进行组合预测。

表1 SPSS曲线估计的参数结果

表2 GMDH自回归不用预测方法结果比较

2 实证分析

利用四川省七大优势产业工业增加值数据做实证分析，该产业仅仅只有1998～2009年的12个年度数据，数据来源于《四川省统计年鉴》。把1998～2007年的数据用于构造预测模型，2008、2009年两年的数据用来检验预测效果。

2.1 SPSS曲线估计预测

应用SPSS软件，选取回归分析——曲线估计，在此界面下选取合适的模型，就可以得到预测值。此时得到如表1结果。

根据检验的f值和概率p值、判定系数R平方的检验原则，其中以判定系数为主要依据，当R平方越趋于1，p值与f值越大越好的原则，我们确定二次曲线和三次曲线为最优模型。

2.2 GMDH自回归预测

根据GMDH自回归预测模型原理，利用软件Knowledge Miner预测。

2.2.1 确定参数

我们需要选取合适的maxtime lag、Model Type等参数值，来确定预测模型。同时根据在模型拟合与预测中，R2、平均绝对百分比误差和预测误差平方和（PESS）这些数据才选取合适的参数。我们根据的原则是R2越接近1，效果越好；平均绝对百分比误差越小越好，控制在5%以内均是可接受水平；预测误差平方和（PESS）越小越好。

表3 模型预测结果

2.2.2 输出模型

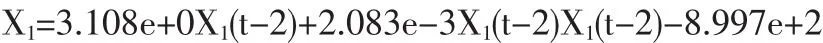
此模型中，R2=0.9995，十分接近 1；MAPE=0.7%；PESS=0.0008，为最优模型。在此基础上进行预测。

但需要注意GMDH有一特点：选取不同的检测集进行预测时，结果有明显差异。因此对2008、2009年直接预测，与两年分步分别得到的结果有较大差距。其中两步预测是基于先预测出一个，在再多一个数据的基础上进一步预测，得到结果。两种方法预测结果如表2所示。

由表2明显可以看出，两步预测优于一步预测，因此我们可以根据实际情况选取合适的方法，对于本文所选数据我们采取两步预测方法。

2.3 组合预测

类似于GMDH自回归建模过程，参数选取选择相同，得到的模型为：

此时 R2=0.9995，十分接近 1；MAPE=0.71%；PESS=0.0006。模型拟合效果较好。

2.4 预测结果比较分析

根据预测得，虽然每个预测模型都趋于最优拟合，但是还是由于样本数据较少，总体误差会比较偏高。也因为数据少，适用模型也较少标准误差最低也只能达到1.23（见表3）。

由表3可知：GMDH自回归模型的预测结果明显优于其他单模型，标准误差为1.23，甚至优于组合预测模型预测结果。分析可知，前面两种单模型的预测结果明显差于GMDH自回归模型，因此我们选择组合预测时，也需要保证单模型预测效果较好。

3 结语

文章中利用SPSS曲线中二次曲线、三次曲线模型和GMDH自回归模型分别对小样本数据进行预测，并将得到的三种单模型利用GMDH进行组合预测。

经预测结果比较得到：GMDH自回归结果最优；其次为组合预测模型预测结果。因此对于小样本数据的预测，GMDH自回归方法效果更好。

GMDH预测方法有其特殊点，即不同的学习集，预测结果明显不同，我们需要根据具体数据情况，选取合适的学习集，以使预测结果最优；组合预测结果不一定最优，其优劣除了取决于组合预测模型外，还取决于单模型预测效果。为了使组合预测效果好，在寻找更优的组合预测模型的同时，必须保证找到合适的、预测效果好的单指标预测模型。

[1]朱家元，杨云，张恒喜，王卓健.基于优化最小二乘支持向量机的小样本预测研究[J].航空学报，2004,(25).

[2]安红刚，胡向东，赵永辉.软土盾构施工地表变形的小样本进化神经网络预测[J].岩土力学，2003，（24）.

[3]徐军辉，汪立新，前培贤.基于最小二乘指出向量机的小样本建模方法研究[J].航空控制，2008，（1）.

[4]薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2004.

[5]刘静思,何跃.基于组合预测模型的工业增加值中长期预测方法研究[J].工业技术经济，2008，（2）.

[6]Mueller J-A,Lemke F.Self-Organising Data Mining[M].Hamburg:Libri,2000.

[7]Madala H R，Ivakhnenko A G.Inductive Learning Algorithms for Complex Systems Modeling[M].Tokyo：CRC Press Inc，1994.

[8]Harrision,P.J.,C.F.Stevens.A Bayesian Approach to Short Term Forecasting[J].Operational Research Quarterly,1971，22.

[9]腾格尔，何跃.基于GMDH组合的中国GDP预测模型研究[J].统计与决策，2010，（7）.

[10]贺昌政.自组织数据挖掘与经济预测[M].北京:科学出版社,2005.

[11]朱兵,贺昌政,肖进.基于GMDH方法的四川民用汽车保有量预测研究[J].现代管理科学，2006，（6）.

F224.7