基于效用函数的高校课程成绩综合评价方法及应用

宋春晖，陈焕东

（海南师范大学 信息科学技术学院，海南 海口 571158）

基于效用函数的高校课程成绩综合评价方法及应用

宋春晖，陈焕东

（海南师范大学 信息科学技术学院，海南 海口 571158）

针对高等学校课程评价的特点，给出了课程权数构造的具体方法，根据评价原则组合多种权数，采用幂平均合成模型对课程成绩进行综合评价，并通过实例应用分析，确定权数合成方法和模型参数.该方法能合理地评价学生的学习效果.

效用函数；综合评价；权数；幂平均合成

高等学校课程的科目多、类型复杂，成绩评定标准存在较大的差异，成绩形式多样，成绩的可比性差，造成课程成绩综合评价的困难.一般的综合评价方法都是采用加权平均的方法计算出课程的平均成绩，其权重一般采用主观赋权法给定，受主观因素影响较大，不能形成具有说服力而且稳定的一套权数[1]，且合成模型也缺乏实际意义，难于全面地评价学生的学习效果.本文采用效用函数综合评价法对课程成绩进行无量纲化处理，根据评价原则构造和组合各种课程的权数，并采用幂平均合成模型对课程成绩进行综合评价，使结果更加合理.

1 效用函数综合评价方法

效用函数综合评价法的简明思想是：采用效用函数将每一个评价指标进行无量纲化处理，变成一个同度量化值，然后再采用合成模型进行加权合成，得出总评价值.其数学模型表示为：

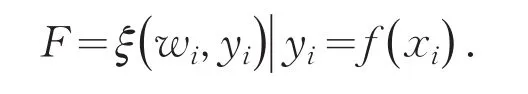
其中，f为第i项评价指标xi的效用函数，也称无量纲化函数或同度量化函数，yi为xi的效用函数评价值，wi为xi的重要性权数，ξ为合成模型.可以得出，效用函数综合评价法是关于f、wi、ξ的理论，分别确定综合评价指标的效用函数、权数和合成模型.其它综合评价方法，如模糊综合评价方法、多元统计综合评价法、灰色系统分析法等，都是效用函数综合评价法的扩展.所以，效用函数综合评价法是一种非常实用、有效的综合评价方法，其评价效率或准确性绝对不逊色于那些数学过程复杂得令人眼花缭乱的方法[2].

每个科目的课程成绩就是一项评价指标，同时，不同课程具有不同的属性，所以，高校课程成绩综合评价属于多指标多属性综合评价问题.

2 课程权数的构造

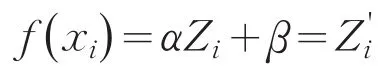
从一般意义上讲，综合评价权数构造时必须反映课程成绩指标的各个属性因素，紧紧围绕着综合评价目的层层展开，列举所有相关的属性因素，并通过综合分析和筛选，确定最后的属性因素作为权项.与课程成绩指标相关的属性因素很多，其中课程学分、课程类型、成绩区分度与综合评价目标最相关，可根据这些因素构造课程成绩权数.

（1）课程学分权数.学分是计算课程学习量的单位，指示该课程的教学时间.不同课程的学分有所差异，反映了不同的学习比重.所以，学分权数是一种典型的比重权数.

（2）课程类型权数.在大学的专业学科课程设计中，一般按课程的功能分为通识教育课程、学科基础课程、专业核心课程、专业拓展课程和实践活动课程等类型.课程类型体现了该课程在学科结构中的作用.所以，课程类型权数反映了不同类型的课程在学科课程结构中重要性.由于课程类型权数本质复杂，一般由教育专家来给定.

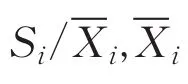
设Ci（i=1，2，…，n）为第i门课程的学分，Ti为第i门课程类型的专家给定权数，n是某一个学习阶段课程的总数，学分权数Wci、课程权数Wti、区分度权数Wdi的归一计算式为：

3 合成模型

将单项评价值yi和权数wi合成总评价值，需要选择科学合理的合成模型ξ，不同合成模型代表了不同的评价思想或评价原则，从而对综合评价结论会产生较大的影响，所以，ξ的选择和wi的合成是综合评价的核心.

3.1 权数的合成

由于Wti、Wci和Wdi是从不同的侧面考虑评价指标的重要性，必须进行合成或组合.组合赋权法可分两类[1]，一类为乘法合成的归一化方法；另一类为线性加权组合法.

（1）乘法合成归一化方法的计算公式为：

这种组合方法由于存在使大者更大，小者更小的“倍增效应”，适合于突出重点课程的评价原则.

（2）线性加权组合法的计算公式为：

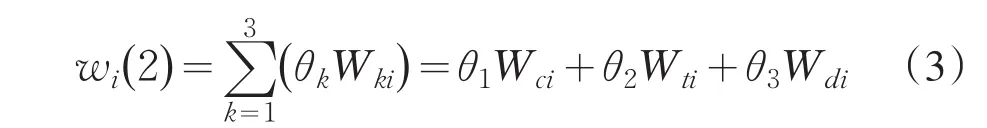
θk=(θ1,θ2,θ3)为3种权的组合权数.这种方法又面临权系数分配的问题.在多属性排序决策问题中，可采用离差平方和最大化赋权法[5]来确定权系数的分配问题.

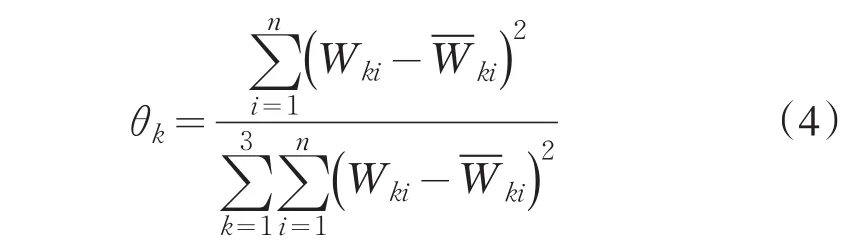
3.2 幂平均合成模型

在效用函数综合评价法中主要采用“幂平均合成”模型.幂平均函数的一般定义为

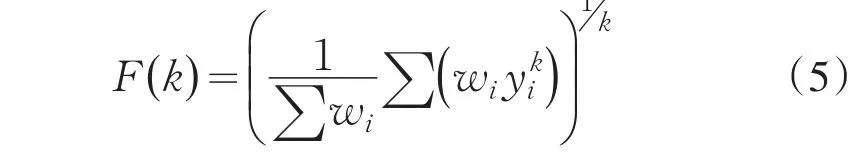
其中，k为幂平均阶数.幂次k可取任意实数值，通常取整数.当k=1时，F（1）为算术平均合成模型；当k=-1时，F（-1）为调和平均合成模型；当k=2时，F（2）为平方平均合成模型.高校的课程综合评价中，灵活地选择一个适当的K值，可体现不同的评价原则.一般而言，取k≤1时，允许“取长补短”，体现鼓励均衡发展的原则；取k＞1时，体现“惩罚落后”，而且k值越大，惩罚的力度越大，体现鼓励突出重点的原则.

4 实例应用

将以上方法应用于某高校电子商务专业二年级某班级（共49名学生）一学期课程（共8门课程）成绩的综合评价中，主要应用步骤如下：

（2）计算各门课程的3种权数：先列出8门课程的学分Ci、由专家给定课程权数Ti、根据原始成绩计算课程的变异权数Vi，然后由（1）式计算出Wci、Wti、Wdi.按（2）式对课程权数进行合成，得出Wi（1）；按（4）式求得组合权数θk（θ1=0.43，θ2=0.09，θ3=0.48），代入（3）式计算出Wi（2）.相关数据见表1.

（3）分别取k=1和k=2、wi=Wi（1）和wi=Wi（2），由（5）式幂平均合成模型对课程成绩进行综合合成，得出不同的综合评价值F（k），又按yi=，得出综合评价值，并按这几种综合评价值给出排序结果O.几种综合评价值的部分相关数据见表2.

表1 课程权数计算及合成数据Tab.1The calculated and combined data of course weight

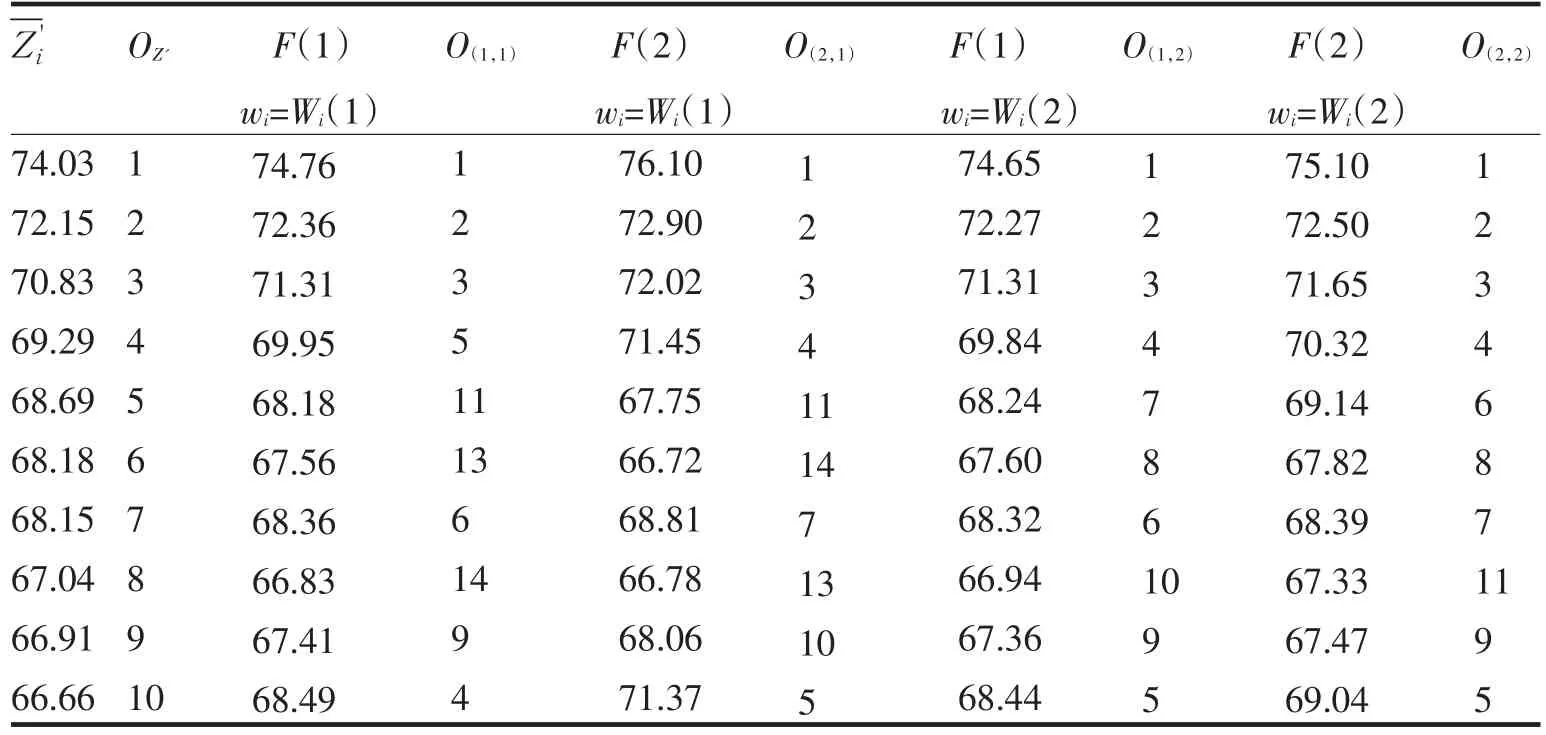
表2 几种综合评价值和排序Tab.2 Several comprehensive evaluation values and their order

从表1的课程权数计算及合成数据来看，Wi（1）比Wi（2）的区分度大，更符合决策对象属性的离散程度尽可能大的原则.从表2的几种综合评价值来看，虽然Wi（1）和Wi（2）有较大的区分度，没有造成总体评价值太大的变化，但对排序结果影响较大.取k=1、wi=Wi（2）更能体现鼓励均衡发展的原则.所以，在高校课程成绩综合评价的实际应用中，基于权数乘法合成和幂平方平均合成模型的效用函数综合评价法，更能体现“全面性、整体性”的均衡发展评价原则，能全面地评价学生的学习效果.

5 结语

基于权数乘法合成和幂平方平均合成模型的效用函数综合评价法能充分体现均衡发展评价原则，既能针对高等学校学生课程成绩评价的特点，解决了不同类型课程之间存在课程性质、考核目标、评分标准和成绩形式差异的问题，又能考虑到学生的学习量和课程的重要性等因素，使评价结果更加合理.

[1]杨宇.多指标综合评价中赋权方法评析[J].统计与决策,2006(13):17-19.

[2]苏为华.多指标综合评价理论与方法问题研究[D].厦门:厦门大学,2000.

[3]Song C H,Huang L Z,Chen H D,et al.A Calculating Method of Weighted Normalized Standard Score[C].Infor⁃mation Technology and Industrial Engineerin,ICIT,2010:973-977.

[4]付靖,赵彦晖,姚继涛.变异系数加权法在评价高校学生成绩中的应用[J].科技资讯,2009(09):195-196.

[5]张荣,刘思峰,刘斌.基于离差最大化客观赋权法的一般性算法[J].统计与决策,2007(24):29-31.

Comprehensive Evaluation Method of College Course Grade and its Application Based on Utility Function

SONG Chunhui，CHEN Huangdong
（College of Information Science and Technology，Hainan Normal University，Naikou571158，China）

This article proposes dimensionless method of constructing course grades and their weights according to the characteristics of course assessment in colleges and universities.Several weights are combined according to evaluation principles,and course grade are evaluated comprehensively by using synthetic model of power mean.The methods of combining weights and the model parameters were also determined by analyzing its application in a specific example.This method can be used to evaluate students’learning reasonably.

utility function；comprehensive evaluation；weight；synthesis of power mean

C 934；G 64

A

1674-4942（2011）02-0224-03

2011-01-16

中央电化教育馆全国教育技术研究课题（063830334）；海南省教育厅科研项目（Hjjsj201010）

毕和平