用初等变换法求r-循环矩阵的逆矩阵
2011-12-07蒋加清
蒋加清
(台州学院 教师教育学院,浙江 临海 317000)
用初等变换法求r-循环矩阵的逆矩阵
蒋加清
(台州学院 教师教育学院,浙江 临海 317000)
首先给出r-循环矩阵的定义与良好的结构,探讨了r-循环矩阵的相应的线性方程组,然后利用矩阵初等行变换求出线性方程组的解,即可求出r-循环矩阵的逆矩阵.该方法不需要计算三角函数,且具有很少的计算量,显得实用、简便.
r-循环矩阵;逆矩阵;线性方程组;初等行变换;阶梯型矩阵
1 预备知识
定义1[1]若A具有形状

则称A为r-循环矩阵,因此A决定于a0,a1,…,an-1及参数r,故可简记为:

特别,当r=1时,就是通常的循环矩阵;当r=-1时,就是通常的反循环矩阵.
如果写作A=(aij)(i,j=0,1,…,n-1),则

观察(1)式对角线上及对角线位置上的那些元素特点,即任何r-循环矩阵,都可以写成:
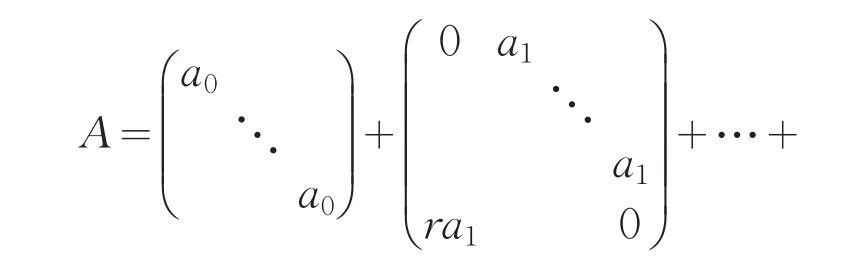


显然E,J,J2,…,Jn-1线性无关,因此A的表达式唯一,即任何r-循环矩阵都可由J的多项式唯一表示.

2 定理与算理

证明因为A=Cr( )a0,a1,…,an-1∈CMr,所以 A=a0J0+a1J+…+an-1Jn-1,欲证r-循环矩阵A的逆矩阵也是r-循环矩阵,只要找到
B=b0J0+b1J+…+bn-1Jn-1,注意到 Jn+k=rJk(k为非负整数)

要使AB=E=J0,为此只须满足下列条件:

对于具体地解线性方程组,消元法是最有效且最基本的方法.消元法解下列方程组的理论根据是线性方程组经初等变换得到同解线性方程组.
将求解线性方程组的消元法转化为对方程组的增广矩阵施行初等行变换化为阶梯形矩阵,这一过程简单明了.
定理2如果矩阵
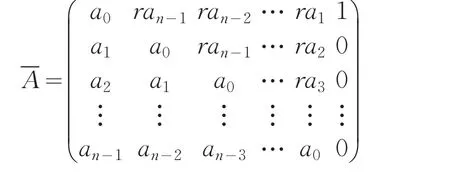

3 算法与例子
由定理1与定理2可知用初等行变换求r-循环矩阵的逆矩阵的算法,其步骤如下:

例1设A=C3(1,-1,-1,1),求A-1.


[1]沈光星.关于某些循环矩阵的特征值[J].应用数学,1991,4(3):76-82.
[2]沈光星.关于r-循环系统的计算复杂性[J].数学研究与评论,1992,12(4):595-598.
[3]钱吉林.高等代数题解精粹[M].北京:中央民族大学出版社,2002:57-58.
[4]蒋加清.关于r-循环矩阵求逆的一种快速算法[J].吉林师范大学学报:自然科学版,2011,32(1):88-89.
[5]何承源.循环矩阵的一些性质[J].数学的实践与认识,2001,31(2):211-216.
[6]江兆林,周章鑫.关于r-循环矩阵的非异性[J].高校应用数学学报,1995,10(2):222-226.
[7]郭运瑞,江兆林.r-循环矩阵逆矩阵的插值法证明[J].广州师院学报:自然科学版,1997,1:22-27.
[8]施敏雪,史美华.关于r-循环矩阵的若干性质[J].浙江教育学院学报,2005,7(4):14-18.
Solving the Inverse of r-circular Matrix by Elementary Operation
JIANG Jiaqing
(Teacher Education College,Taizhou University,Linhai317000,China)
This paper explored the related set of linear equations ofr-circular matrix,by giving its definition and good structure and then using the elementary row operation of matrix to work out the solution of a set of linear equations-the inverse matrix ofr-circular matrix.The method is practical and convenient with no needs to calculate trigonometric func⁃tion and small calculation amount.
r-circular matrix;inverse matrix;set of linear equations;elementary row operation;echelon form matrix
O 151
A
1674-4942(2011)04-0383-03
2011-07-25
毕和平
