一类高阶微分系统谱的带权估计

黄振明

（苏州市职业大学 基础部，江苏 苏州 215104）

一类高阶微分系统谱的带权估计

黄振明

（苏州市职业大学 基础部，江苏 苏州 215104）

考虑一类高阶微分系统谱的带权估计，利用矩阵运算、分部积分、测试函数、Rayleigh定理和不等式估计等方法，获得了用前n个谱来估计第n+1个谱的上界的不等式，且其估计系数与区间的度量无关，其结论是文献定理的进一步拓展.

微分系统；谱；特征函数；带权估计

设(a,b)⊂R是一个有界区间，考虑如下微分系统

近年来，对单个微分方程的谱估计已取得了一系列成果[1-6]，笔者参照并改进文[7-8]中的讨论方法，进一步推广到对高阶微分系统（1）的谱估计，其中将权推广至x的任意函数s（x），获得了用前n个谱来估计第n+1个谱的上界的不等式，其估计系数与区间的度量无关，文[9]讨论的问题仅是问题（1）中当s=1，t=2时的一种特例，因此本文结论可视作是文献[1-6]和[9]的进一步推广，在微分方程的谱理论研究中有着广泛的参考价值[10].

利用（5）和多次分部积分，有

1 引理

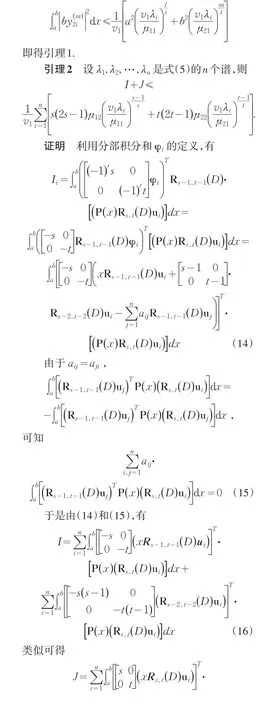
2 主要结果

[1]Hile G H,Yen R Z.Inequalities for Eigenvalues of the Bi⁃harmonic Operator[J].Pacific J Math,1984,112(1):115-132.

[2]吴平,钱椿林.梁横向振动方程的离散特征值估计[J].江苏广播电视大学学报,2001,12(6):40-42.

[3]吴平,钱椿林.高阶常微分方程特征值的上界估计[J].苏州铁道师院学报:自然科学版,2001,18(3):3-9.

[4]黄振明.一类线性微分算子谱的带权估计[J].廊坊师范学院学报:自然科学版,2009,9(4):8-10,13.

[5]陈静,钱椿林.任意阶微分算子第二特征值的上界估计[J].淮阴工学院学报:自然科学版,2006,15(3):13-17.

[6]卢亦平,钱椿林.微分方程带一般权的第二特征值的上界估计[J].长春大学学报:自然科学版,2009,19(10):7-10.

[7]黄振明.一类六阶微分系统特征值的上界估计[J].甘肃联合大学学报:自然科学版,2007,21(1):11-15.

[8]赵晓苏,钱椿林.六阶微分系统带权第二特征值的上界[J].长春大学学报:自然科学版,2010,20(8):10-13.

[9]吴平,钱椿林.一类微分系统特征值的上界估计[J].苏州市职业大学学报,2007,18(1):79-82.

[10]Protter M H.Can one hear the shape of a drum?[J].SI⁃AM Rev,1987,29(2):185-197.

Weighted Estimate of Spectra for a Class of Higher-Order Differential System

HUANG Zhenming

（Suzhou Vocational University，Suzhou215104，China）

In this paper,estimate of spectra for a class of higher-order differential system is considered.The inequality of the upper bound of the(n+1)th spectrum is estimated from the formernspectra by using matrix operation,integration by parts,trial function,Rayleigh theorem and inequality estimate,etc.The estimate coefficients do not depend on the measure of the domain in which the problem is concerned.The results expanded the theorems in the bibliography.

differential system；spectrum；eigenfunction；weighted estimate

O 175.1

A

1674-4942（2011）04-0379-04

2011-08-25

毕和平