曲线设计的一种细分格式的改进

王晶昕，魏春玮

（辽宁师范大学 数学学院，辽宁 大连 116029）

曲线设计的一种细分格式的改进

王晶昕，魏春玮

（辽宁师范大学 数学学院，辽宁 大连 116029）

细分方法是曲线曲面造型中的一项重要技术，在计算机辅助几何设计和计算机图形学等领域得到了广泛应用.本文提出一种非静态割角细分方法，该方法的极限曲线具有保凸性，凸包性等与Bézier方法类似的性质.可以验证当参数取不同的特定值时，该方法为Chaikin割角法和Riesenfeld割角法等.另外文中通过调整参数得到了一些形状各异的曲线.

曲线；细分；割角；逼近

细分曲线是由初始控制多边形通过重复逼近或插值得到的[1].由于细分曲线具有任意拓扑网格和从离散到离散的特点，从而在计算机辅助几何设计和计算机图形学中得到了广泛应用.曲线的细分主要可以分为逼近型和插值型两类.插值型细分是在保留原控制点的同时不断加入新点，所以插值细分又可以看成是补角过程；相反的，逼近型细分是通过对原始控制多边形不断割角磨光而得到的.

割角思想最早可以追溯到上世纪五十年代，De Rham在他的论文中使用割角法来描述光滑曲线[2].其后的几十年中割角细分法得到了广泛的研究，1974年，在美国Utah大学举行的CAGD国际会议上，Chaikin提出了一种曲线的快速生成方法：割角法细分[3].1980年，Lane和Riesenfeld[4]把Chaikin细分方法推广到对空间多边形的所有边都同时取中点的递归割角法.这两种方法后来被证明了分别为二次和三次B样条曲线.他们都属于均匀稳定的细分方法，即，对每一层以及整个多边形或网格都应用同一细分规则.虽然这种方法都简单易行，但是也存在着一定的局限性，例如，不具备局部可调性、不易表现几何特性以及造型能力差等.1996年Gregory和Qu Ruibin[5]提出了非均匀割角法，这种方法具备了局部可调整性.本文推广上述方法，提出了一种新的细分格式，其中所带的两个参数取自了[0，1]，可以验证前面那些方法是这种方法的特例.本方法得到的极限曲线具有良好的保凸性、凸包性等几何性质.本文还讨论了这种方法的收敛性，最后给出一些具体实例.

1 基本格式

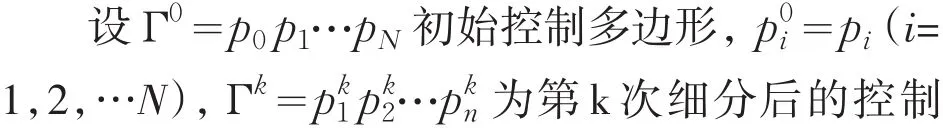
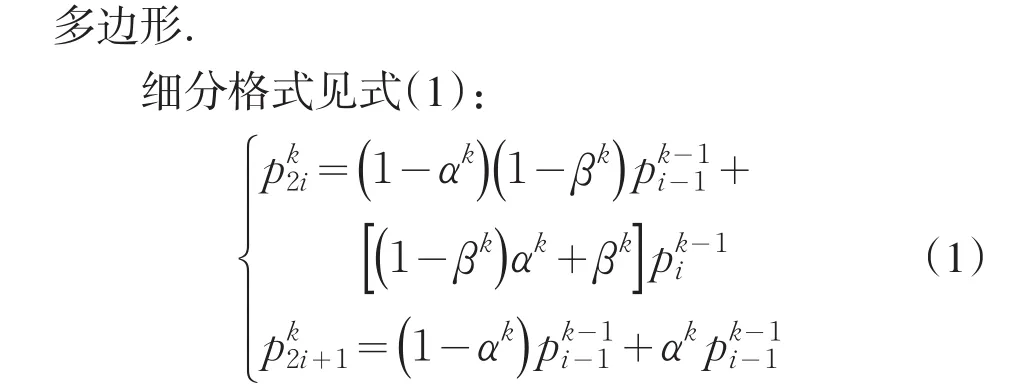
其中，αk∈[0,1],βk∈[0,1] 参数 αk,βk可以调整曲线的形状以及对初始控制多边形的逼近程度.参数越大，曲线与初始控制多边形的逼近程度越弱，参数越小，曲线与初始控制多边形的逼近程度增强.

拓扑规则如图1所示，其中实线为第k-1层的控制多边形，虚线为经过一次细分后第k层的控制多边形.

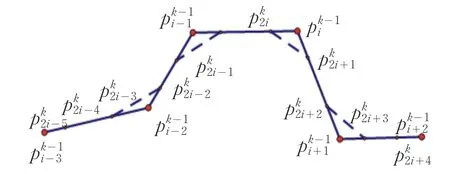
图1 拓扑规则Fig.1 Topological structure

2 收敛性分析

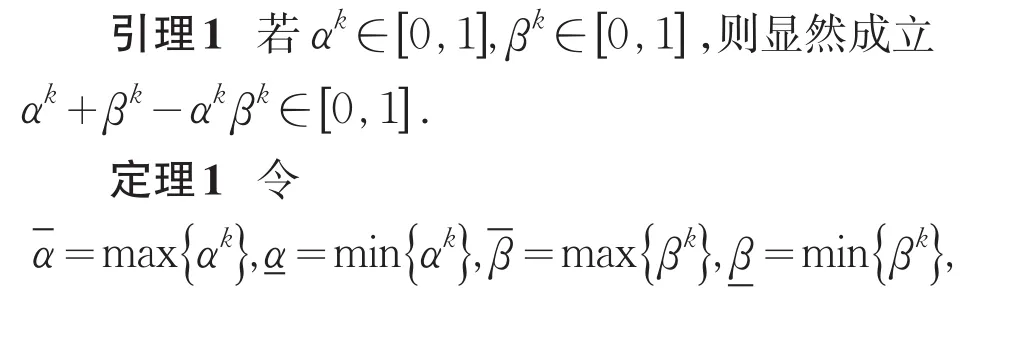
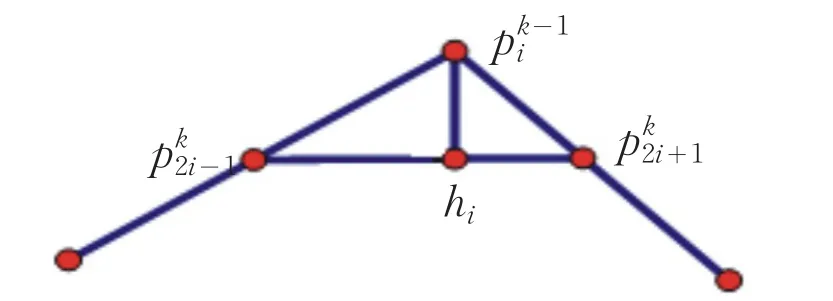
图2p到Γk+1的距离Fig.2 The distances betweenpkiandΓk+1

3 极限曲线的几何性质

应用本文的方法产生的细分曲线具有以下良好的几何性质.

性质1保凸性，若初始控制多边形Γ0为凸的，则细分曲线也是凸的.

证明由于初始控制多边形Γ0是凸的，所以多边形Γ0的内角都小于π，由细分规则可知，每次细分后的多边形的内角都小于π，因此多边形Γk也是凸的，既细分曲线也是凸的.

性质2凸包性，细分曲线落在初始控制多边形 Γ0的凸包内，若所有顶的重合时，曲线也缩为一点.

证明由细分规则可知Γk位于Γk-1的凸包内，因此Γk一定位于Γ0的凸包内，于是当k→∞时，极限曲线 Γ∞一定位于Γ0的凸包内.

性质3局部性，变动初始控制多边形Γ0的一个顶点，仅影响曲线在该点附近的部分.

证明由细分的规则可知，每个新的控制点的产生仅依赖于相邻的两个旧控制点，且控制多边形的每条边上仅产生2个新的控制点，也就是说每个旧控制点仅影响下一层的4个控制点，因此变动初始控制多边形Γ0的一个顶点，仅影响曲线在该点附近的部分.

4 实例分析

本节通过实例来展现本章方法的强大曲线造型能力.首先通过调整参数研究参数对曲线形状的影响，其次介绍初始控制多边形为正方形时，取不同的参数生成形状各异的曲线.

从图3—图6可以看出，细分得到的曲线都与控制多边形相切，并且当参数越大，曲线与初始控制多边形的逼近程度越弱，但曲线的整体感增强，当参数越小，曲线与初始控制多边形的逼近程度增强，而曲线的整体感减弱.

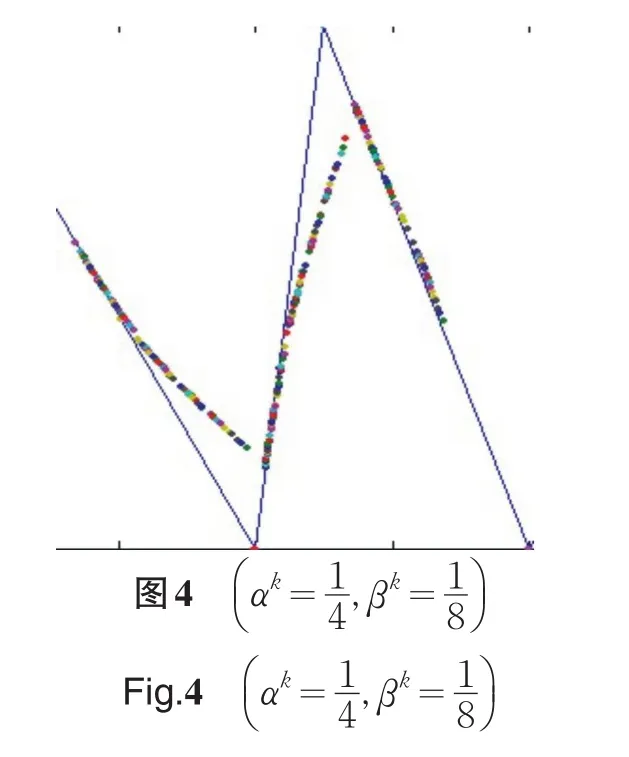
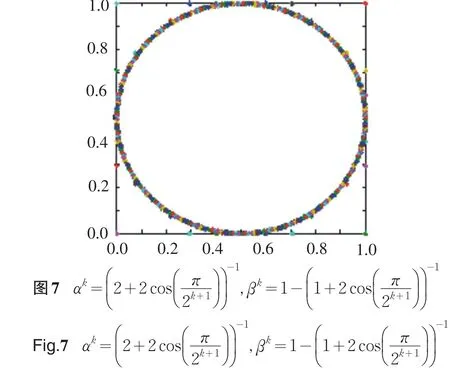
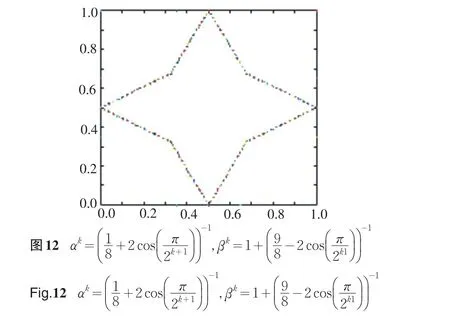
本细分法具有强大的造型能力，下面介绍应用本细分法生成的一些有趣的曲线.初始控制多边形都为正方形，取不同的参数值产生形状各异的曲线，见图7—图12.

[1]王仁宏,李崇军,朱春刚.计算几何教程[M].北京:科学出版社,2008:199-234.

[2]朱心雄.自由曲线造型技术[M].北京:科学出版社,2000:236-249.

[3]Chaikin.An algorithm for high speed curve generation[J].Computer Graphics And Image Processing,1974,3(1):346-349.

[4]Lane J M,Riesenfeld R F.A theoretical development for the computer generation and display of piecewise poly sur⁃faces[J].Pattern Anal Mach Intelling,1980,2(1):35-45.

[5]Gregory J A,Qu Ruibin.Nonuniform corner cutting[J].Computer Aider Geometric Design,1996,13(8):763-772.

[6]施法中.计算机辅助几何设计与非均匀有理B样条[M].北京:高等教育出版社,2001,8(1):214-243.

An Improvement Subdivision Scheme for Curve Design

WANG Jingxin，WEI Chunwei
（School of Mathematics，Liaoning Normal University，Dalian116029，China）

Subdivision is one important technology in curves and surfaces modeling,and subdivision has been widely used in computer aided geometric design and computer graphics.In this paper a new subdivision scheme—Non-statio⁃nery corner cutting subdivision scheme was proposed.Compared with the other existing methods,such as Bézier this scheme also has convexity-preserving.By choosing appropriate parameters,this subdivision scheme could be content Chaikin and Riesenfeld scheme.In this thesis some different curves were obtained by choosing appropriate parameters.

Curves；subdivision；corner cutting；approximating

O 241.5

A

1674-4942（2011）04-0375-04

2011-09-21

国家自然科学基金项目（11071031）

毕和平